CS229 学习笔记之二：分类与逻辑回归

发表于 2018-03-15 分类于人工智能，课程笔记阅读次数：本文字数： 1.5k 阅读时长 ≈ 5 分钟

本篇博客为 CS229 学习笔记第二部分，主题是：分类与逻辑回归。

之前我们讨论的是回归问题，即输出是连续值，现在我们来讨论输出是离散值的分类问题。本节我们将专注于二元分类问题，即输出 $y$ 只能取 $0$ 和 $1$ 两个值。

逻辑回归

如果将线性回归模型直接应用于分类问题，会产生取值不在 0 和 1 之间的问题，所以我们引入逻辑回归模型： \[ h_{\theta}(x) = g(\theta^Tx) = \frac 1 {1+e^{-\theta^Tx}} \]

其中 \[ g(z) = \frac 1 {1+e^{-z}} \] $g(z)$ 被称为逻辑函数或 S 型函数，其图像如下：

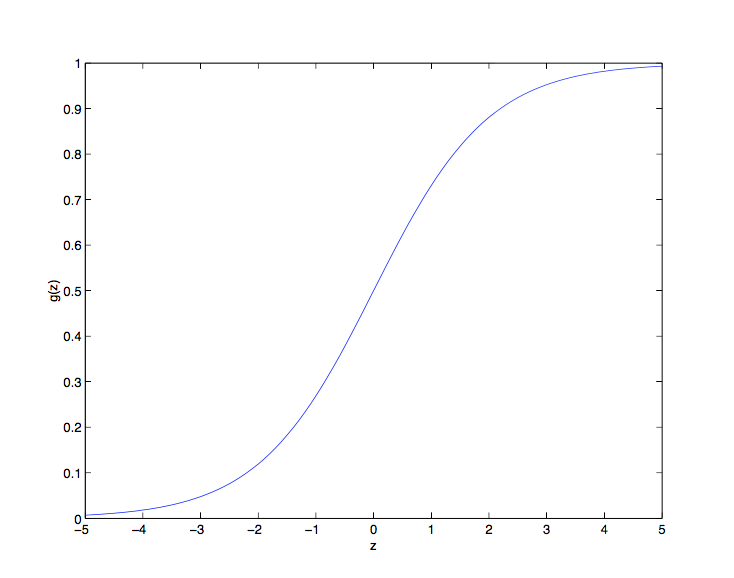
可以看到，当 $z \to +\infty$ 时 $g(z)$ 趋向于 $1$，当 $z \to -\infty$ 时 $g(z)$ 趋向于 $0$，即 $g(z)$ 的值域为 $(0,1)$，至于为什么要选择这个函数，在之后会作出解释。

这里先给出一个关于 S 型函数求导的有用性质： \[ \begin{align*} g'(z) &= \frac d {dz} \frac 1 {1+e^{-z}} \\ &= \frac 1 {(1+e^{-z})^2} (e^{-z}) \\ &= \frac 1 {1+e^{-z}} \cdot \left( 1- \frac 1 {1+e^{-z}}\right) \\ &= g(z)(1-g(z)) \end{align*} \] 确定了模型之后，我们需要找到合适的 $\theta$ 的值。这里采用之前使用的最大似然法来选择参数（假设函数可以直接看作概率分布）。

首先，二元分类符合伯努利分布，我们假设： \[ \begin{align*} P(y=1 \mid x ;\theta) &= h_{\theta}(x)\\ P(y=0 \mid x ;\theta) &= 1-h_{\theta}(x) \end{align*} \]

将上面的公式合二为一，得到： \[ P(y \mid x ; \theta) = (h_{\theta}(x))^y(1-h_{\theta}(x))^{1-y} \] 假定 $m$ 个样本之间相互独立，我们可以得到 $\theta$ 的似然函数如下： \[ \begin{align*} L(\theta) &= p(\vec y \mid X; \theta) \\ &= \prod_{i=1}^m p(y^{(i)} \mid x^{(i)};\theta) \\ &= \prod_{i=1}^m \left(h_{\theta}(x^{(i)})\right)^{y^{(i)}}\left(1-h_{\theta}(x^{(i)})\right)^{1-y^{(i)} } \end{align*} \]

与之前类似，为了计算方便，我们使用对数似然函数来进行最大化分析： \[ \begin{align*} \ell(\theta) &= \log L(\theta) \\ &= \sum_{i=1}^m y^{(i)}\log h(x^{(i)})+(1-y^{(i)} )\log (1-h(x^{(i)})) \end{align*} \] 下面要做的是找到 $\theta$ 使得 $\ell(θ)$ 最大，由于这里是找最大值而非最小值，所以使用梯度上升（gradient ascent），参数的更新规则是 $\theta := \theta +\alpha \nabla_\theta \ell(\theta)$，对于随机梯度上升（每次只考虑一个样本），求导过程如下： \[ \begin{align*} \frac{\partial}{\partial \theta_j}\ell(\theta) &= \left(y \frac 1 {g(\theta^Tx)}-(1-y)\frac 1 {1-g(\theta^Tx)}\right)\frac{\partial} {\partial \theta_j}g(\theta^Tx)\\ &= \left(y \frac 1 {g(\theta^Tx)}-(1-y)\frac 1 {1- g(\theta^Tx)}\right)g(\theta^Tx)(1-g(\theta^Tx))\frac{\partial}{\partial \theta_j}\theta^Tx \\ &= \left(y(1-g(\theta^Tx))-(1-y)g(\theta^Tx)\right)x_j\\ &= \left(y-h_\theta(x)\right)x_j \end{align*} \]

在计算过程中我们使用到了 S 型函数的求导性质。

综上所述，我们得到随机梯度上升的更新规则是： \[ \theta_j := \theta_j +\alpha\left(y^{(i)}-h_\theta(x^{(i)})\right)x^{(i)}_j \]

这个公式和线性回归中梯度下降的公式表面上看是一样的，但实际上两者的 $h_\theta(x)$ 有所不同，关于更加深层次的讨论，请参看之后的 GLM 模型章节。

牛顿方法

下面我们介绍另外一种算法来求解 $\ell (\theta)$ 的最大值，称为牛顿方法。我们可以通过如下的几张图来理解牛顿方法：

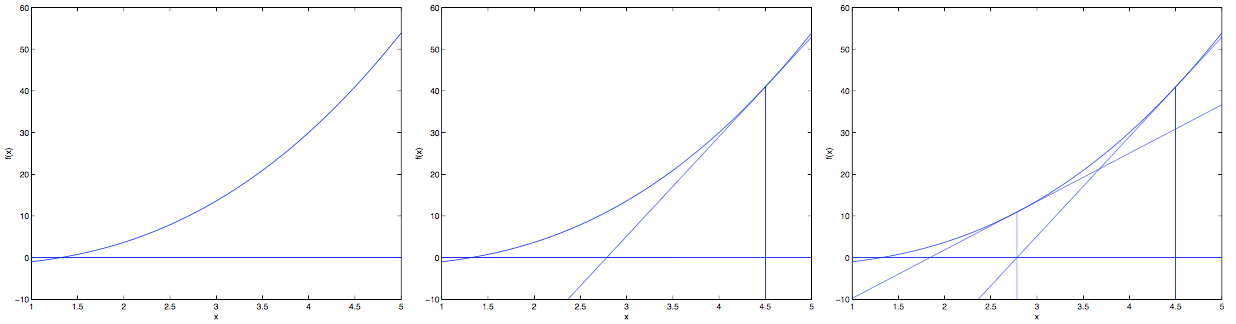
对于梯度下降，每次只是在梯度方向上下降一小步（取决于学习速率），而牛顿方法是一直下降到导数（切线）和 $\theta$ 轴交界的那个 $\theta$。因此牛顿方法的更新规则是： \[ \theta := \theta - \frac {f(\theta)} {f' (\theta)} \] 下面我们将牛顿方法应用于逻辑回归，我们需要找到 $\ell (\theta)$ 的最大值，即 $\ell '(\theta)=0$，因此令 $f(\theta)=\ell '(\theta)$，我们可以得到逻辑回归的牛顿方法更新公式： \[ \theta := \theta - \frac {\ell '(\theta)} {\ell '' (\theta)} \] 而对于 $$ 为向量的情况，牛顿方法的多维形式如下（又被称为牛顿-拉夫逊方法）： \[ \theta := \theta - H^{-1} \nabla_\theta \ell(\theta) \]

其中 $\ \nabla_\theta \ell(\theta)$ 是 $\ell(\theta)$ 对于每个 $\theta_i$ 的偏导数构成的向量。$H$ 是一个 $(n+1)\times (n+1)$ 的矩阵（包括截距项），称为海森矩阵，其中的每一项定义为： \[ H_{ij}=\frac {\partial^2 \ell(\theta)} {\partial \theta_i \partial \theta_j} \] 和（批量）梯度下降相比，牛顿方法会带来更快的收敛速度和更少的迭代次数。虽然每次迭代由于要计算$H^{-1}$，导致计算量较大，但对于参数数量不是特别大的情况，总的来说它还是更快的。将牛顿方法用于求解逻辑回归的对数似然函数最大值，也被称为费雪评分。

感知器学习算法

下面介绍另一种二分类方法：感知器学习算法。其假设函数为： \[ h_\theta(x)=g(\theta^Tx)=\left\{ \begin{align*} & 1 \quad \text{if} \;\theta^Tx \ge 0\\ & 0 \quad \text{if} \;\theta^T x < 0 \end{align*} \right. \]

可以看到 $g(z)$ 是逻辑回归的 s 型函数的简化形式：

逻辑函数是连续的在 [0,1] 区间上
感知器直接非 0 则 1

感知器学习算法的参数更新规则如下： \[ \theta_j := \theta_j +\alpha\left(y^{(i)}- h_\theta(x^{(i)})\right)x^{(i)}_j \] 19世纪60年代，感知器被看作是大脑工作中独立神经元的粗糙的模型，虽然直观看上去，感知器和之前看到的逻辑回归或线性回归很像，但是其实是非常不一样的算法。因为对于感知器，很难赋予一种有意义的概率解释，或使用最大似然估计算法来进行推导。

逻辑回归

牛顿方法

感知器学习算法

思维导图