CS229 学习笔记之四:生成学习算法
本篇博客为 CS229 学习笔记第四部分,主题是:生成学习算法。
算法概述
到目前为止,我们讨论的学习算法都是直接对 \(p(y\mid x;\theta)\) 建模,即对于给定的 \(x\),\(y\) 的条件分布。这里我们将讨论一种不同类型的学习算法。
学习算法可以分为两种,一种是尝试去直接学习得到 \(p(y \mid x)\)(例如逻辑回归),或者尝试去学习直接将输入映射到0或1的方法(例如感知器算法),这种算法被称为判别学习算法;而另外一种学习算法被称为生成学习算法,这种算法会尝试对 \(p(x\mid y)\) 以及 \(p(y)\) 建模。
当我们为 \(p(y)\) (被称为class priors) 和 \(p(x\mid y)\) 建模后,我们的算法会使用贝叶斯定理来计算给定 \(x\) 后 \(y\) 的后验概率: \[ p(y\mid x) = \frac {p(x\mid y)p(y)} {p(x)} \]
其中分母可以通过 \(p(x) = p(x|y=1)p(y=1) + p(x|y=0)p(y=0)\) 得到(针对二分类)。
对于分类问题,我们需要对每种 \(y\) 的情况分别进行建模。当有一个新的 \(x\) 时,计算每个 \(y\) 的后验概率,并取概率最大的那个 \(y\) 作为预测输出。
由于只需要比较大小,而\(p(x)\) 对于大家都是一样的,所以可以忽略分母,得到下式: \[ \begin{align*} \arg\max_{y} p(y|x) &= \arg\max_{y} \frac {p(x| y)p(y)} {p(x)}\\ &= \arg\max_{y} p(x| y)p(y) \end{align*} \]
高斯判别分析
我们学习的第一个生成学习算法叫高斯判别分析(GDA)。在这个模型中,我们会假设 \(p(x|y)\) 属于多元正态分布。在介绍 GDA 之前,首先简单介绍一下多元正态分布的属性。
多元正态分布
多元正态分布是在 n 维空间中的,其参数有:
- 均值向量:\(\mu \in \mathbb{R}^{n}\)
- 协方差矩阵:\(\Sigma \in \mathbb{R}^{n \times n}\),\(\Sigma \ge 0\) 对称且为半正定(所有特征值均不小于零)
我们将分布记作 \({\cal N} (\mu,\Sigma)\) ,其概率密度公式为: \[ p(x;\mu, \Sigma) = \frac {1} {(2\pi)^{n/2} |\Sigma |^{1/2}} \exp \left(- \frac{1} {2} (x-\mu)^{T}\Sigma^{-1}(x-\mu)\right) \]
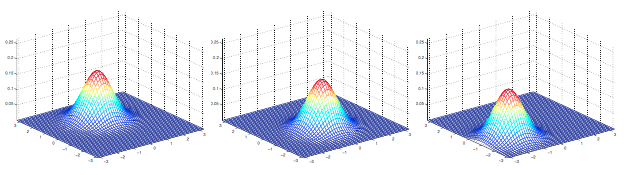
其中 \(|\Sigma|\) 表示 \(\Sigma\) 的行列式。对于一个属于多元正态分布 \({\cal N} (\mu,\Sigma)\) 的随机变量 \(X\),根据期望与方差的计算公式可以得到: \[ \begin{align*} E[X] &= \int_x xp(x; \mu, \Sigma)dx \\ &=\mu \\ Cov(X) &= E[(X - E[X])(X - E[X])^T] \\ &= \Sigma \end{align*} \] 下面给出一些二元高斯分布的概率密度图像:
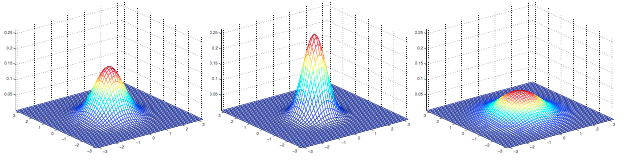
左边的图显示的分布均值为 \(0\)(\(2\times1\)的向量),协方差矩阵为 \(I\) (\(2 \times 2\)的单位矩阵)。这样的正态分布又被称为标准正态分布;中间的图显示的分布均值为 \(0\) 且 \(\Sigma = 0.6 I\);右边的图显示的分布 \(\Sigma = 2 I\)。可以看到随着 \(\Sigma\) 的变大,分布变得越来越“展开”,看起来就像变得越来越“扁”。
让我们来看看更多的例子:

上图表示的分布均值均为 \(0\),对应的协方差矩阵为: \[ \Sigma =\left[ \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array} \right ]; \Sigma =\left[ \begin{array}{cc} 1 & 0.5 \\ 0.5 & 1 \end{array} \right ]; \Sigma =\left[ \begin{array}{cc} 1 & 0.8 \\ 0.8 & 1 \end{array} \right ] \] 左边的图就是标准正态分布,而可以看到随着非对角线上数值的增大,分布在45度方向上压缩的幅度越大,通过下面的轮廓图可以更清楚地展现这个特点:
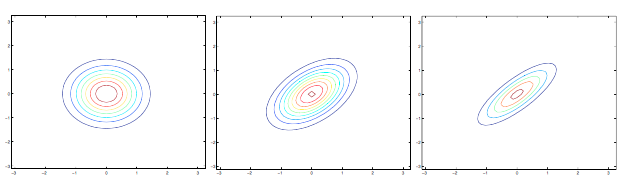
下面是另一组例子:
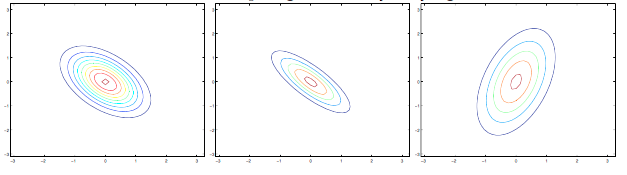
上图对应的协方差为: \[ \Sigma =\left[ \begin{array}{cc} 1 & -0.5 \\ -0.5 & 1 \end{array} \right ]; \Sigma =\left[ \begin{array}{cc} 1 & -0.8 \\ -0.8 & 1 \end{array} \right ]; \Sigma =\left[ \begin{array}{cc} 3 & 0.8 \\ 0.8 & 1 \end{array} \right ] \] 从左图和中图可以看到,随着元素值的减小(绝对值变大),分布在相反的方向上“压缩”得越明显;而在右图中我们改变了对角线上的元素值,分布变得更趋近于椭圆。
在最后一组例子中,令 \(\Sigma = I\),通过改变 \(\mu\) ,我们可以移动分布的中心:
总而言之,多元正态分布与正态分布一样是钟型曲线,两个参数会影响分布的位置与形状: + \(\mu\) 会影响分布的位置(平移) + \(\Sigma\) 会影响分布的形状
高斯判别分析模型
对于一个分类问题,输入变量 \(x\) 是连续随机变量,我们可以使用高斯判别分析(GDA)模型,对 \(p(x| y)\) 使用多元正态分布建模,模型如下: \[ \begin{align*} y &\sim \text{Bernoulli} (\phi) \\ x| y=0 &\sim \cal{N} (\mu_0, \Sigma) \\ x| y=1 &\sim \cal{N} (\mu_1, \Sigma) \\ \end{align*} \] 其概率密度如下: \[ \begin{align*} p(y) &= \phi^y(1-\phi)^{1-y} \\ p(x| y=0) &= \frac{1}{(2\pi)^{n/2}|\Sigma|^{1/2}}\exp\left(-\frac 1 2 (x-\mu_0)^T\Sigma^{-1}(x-\mu_0)\right) \\ p(x| y=1) &= \frac{1}{(2\pi)^{n/2}|\Sigma|^{1/2}}\exp\left(-\frac 1 2 (x-\mu_1)^T\Sigma^{-1}(x-\mu_1)\right) \end{align*} \]
这里模型的参数包括 \(\phi, \Sigma, \mu_0, \mu_1\),注意两个分布共享同一个协方差矩阵。
数据的对数似然函数如下: \[ \begin{align*} \ell(\phi,\mu_0, \mu_1,\Sigma) &= \log \prod_{i=1}^mp(x^{(i)},y^{(i)};\phi,\mu_0\mu_1,\Sigma) \\ &= \log \prod_{i=1}^mp(x^{(i)} | y^{(i)};\mu_0,\mu_1,\Sigma) p(y^{(i)};\phi) \end{align*} \]
通过最大化 \(\ell\),得到参数的极大似然估计为: \[ \begin{align*} \phi &= \frac 1 m \sum_{i=1}^m 1\{y^{(i)} = 1\} \\ \mu_0 &= \frac{\sum_{i=1}^m 1\{y^{(i)}=0\}x^{(i)}}{\sum_{i=1}^m 1\{y^{(i)}=0\}} \\ \mu_1 &= \frac{\sum_{i=1}^m 1\{y^{(i)}=1\}x^{(i)}}{\sum_{i=1}^m 1\{y^{(i)}=1\}} \\ \Sigma &= \frac 1 m \sum_{i=1}^m (x^{(i)}-\mu_{y^{(i)}})(x^{(i)}-\mu_{y^{(i)}})^T \end{align*} \] 用图形来表示,该算法可以表示为下图:
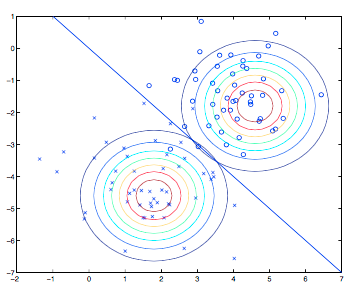
图中展示的是训练集,求得的高斯分布拟合至数据中,将数据分为了两类。注意两个高斯分布的形状相同,因为它们共享同一个协方差矩阵,但是它们的均值不同。
图中的直线表示决策边界:\(p(y=1|x) = 0.5\),在该边界的一侧,我们预测 \(y=1\) 是最可能的输出,在另一侧,则预测 \(y=0\)。
高斯判别分析与逻辑回归
高斯判别分析与逻辑回归之间有着有趣的关系。如果我们将 \(p(y=1 |x; \phi,\mu_0,\mu_1, \Sigma)\)表示为 \(x\) 的函数,可以得到:
\[ p(y=1 | x;\phi,\Sigma,\mu_0,\mu_1) = \frac 1 {1+\exp(-\theta^T x)} \]
这与逻辑回归的形式完全相同。但一般来说,对于相同的数据集两种算法会给出不同的边界,究竟哪一个更好呢?
一个有趣的结论是:
如果 \(p(x| y)\) 属于多元高斯分布(共享 \(\Sigma\)),那么 \(p(y| x)\) 一定是逻辑函数,反之不成立。
上述结论表明高斯判别分析相较于逻辑回归提出了更强的假设。如果这些假设都是正确的,那么高斯判别分析得到的结果会更好,是更好的模型。特别地,当 \(p(x|y)\) 属于多元高斯分布(共享 \(\Sigma\)),GDA 是渐近有效的。这说明在数据量比较有限的情况下,没有算法能比 GDA 的表现更好。因此,在这种情况下,GDA 相比逻辑回归是一个更好的算法,即使对于较少的训练集,也可以取得更好的效果。
相反,因为进行了更弱的假设,所以逻辑回归有更好的鲁棒性,对于错误的模型假设不那么敏感。有很多不同的假设会导致 \(p(y| x)\) 是逻辑函数的形式,比如泊松分布。但是如果我们对于这样的数据使用 GDA,那么结果会变得不可预测。
总结一下,GDA 进行了更强的模型假设并且数据有效性更高(需要更少的数据来学习),但其前提条件是模型假设正确或近似正确;逻辑回归进行较弱的假设,对于模型假设偏离的鲁棒性更好。如果数据集实际上不是高斯分布,那么在数据有限的情况下,逻辑回归一般会表现得比 GDA 更好。因此,实际中使用逻辑回归的情况比 GDA 多得多。
朴素贝叶斯算法
算法概述
在高斯判别分析中,输入是连续变量。现在我们要谈谈一个不同的生成学习算法,其中 \(x\) 是离散变量。
让我们以识别垃圾邮件为例,这类问题被称为文本分类问题。假设我们有一个训练集(已经标记好了是否为垃圾邮件的邮件集合),我们首先需要构建表示一封邮件的特征向量。
我们通过如下方式表示特征向量:其长度为词表的长度,词表为所有可能出现的词的集合,一般通过训练集生成。如果这封邮件包含了第 i 个词,\(x_i = 1\),否则 \(x_i = 0\)。下图为一个简单的例子: \[ x=\left[\begin{array}{c}{1} \\ {0} \\ {0} \\ {\vdots} \\ {1} \\ {\vdots} \\ {0}\end{array}\right] \quad \begin{array}{l}\text{a} \\ {\text {aardvark }} \\ {\text {aardwolf }} \\ {\vdots} \\ {\text {buy }} \\ {\vdots} \\ {\text {zygmurgy }}\end{array} \] 选择好特征向量后,我们需要来构建生成模型。但考虑到 \(x\) 是一个高维向量,因此如果直接对 \(p(x|y)\) 建模,那么会得到一个参数向量的维数极高的多项分布,使计算过于复杂。
因此,我们需要做一个强力的假设,假设给定 \(y\) 时, 每一个 $x_i $ 是条件独立的。这个假设被称为朴素贝叶斯假设,其引出的算法被称为朴素贝叶斯分类器。注意是条件独立而不是独立,即仅在给定 \(y\) 的情况下独立。
现在我们有(以50000维度为例): \[ \begin{align*} p(x_1,\ldots,x_{50000}\mid y) &= p(x_1 | y) p(x_2 | y,x_1)p(x_3 | y,x_1,x_2)\cdots p(x_{50000} | y,x_1, \ldots, x_{49999})\\ &=p(x_1 | y)p(x_2 | y) p(x_3 | y)\cdot p(x_{50000} | y)\\ &= \prod_{j=1}^np(x_j| y) \end{align*} \]
第一个等式来自于概率的基本性质;第二个等式则使用了朴素贝叶斯假设。即使这个假设在现实中不一定成立,但其实际的效果还是不错的。
模型包含了以下三个参数: \[ \begin{align*} \phi_{i|y=1} &= p(x_i = 1 | y=1) \\ \phi_{i|y=0} &= p(x_i = 1 | y=0) \\ \phi_y &= p(y = 1 ) \end{align*} \] 和之前一样,给定一个训练集 \(\{(x^{(i)},y^{(i)}); i=1,\dots,m\}\),我们可以写出如下的联合似然函数
\[ \mathcal{L} (\phi_y,\phi_{i|y=0},\phi_{i|y=1}) = \prod_{i=1}^m p(x^{(i)},y^{(i)}) \]
对这个联合似然函数进行最大似然分析,得到的参数值如下: \[ \begin{align*} \phi_{j|y=1} &= \frac{\sum_{i=1}^m 1\{x_j^{(i)}=1 \wedge y^{(i)}=1\}}{\sum_{i=1}^m 1\{y^{(i)}=1\}}\\ \phi_{j|y=0} &= \frac{\sum_{i=1}^m 1\{x_j^{(i)}=1 \wedge y^{(i)}=0\}}{\sum_{i=1}^m 1\{y^{(i)}=0\}} \\ \phi_y &= \frac {\sum_{i=1}^m 1\{y^{(i)} = 1\}}{m} \end{align*} \]
这些结果的得出是很自然的,从概率的角度也可以很好地解释。得到了这些参数之后,为了对一个新的输入 \(x\) 进行预测,我们可以计算: \[ \begin{align*} p(y=1 | x) &= \frac{p(x| y=1)p(y=1)}{p(x)} \\ &= \frac {(\prod_{i=1}^n p(x_i | y=1))p(y=1)}{(\prod_{i=1}^n p(x_i | y=1))p(y=1)+(\prod_{i=1}^n p(x_i | y=0))p(y=0)} \end{align*} \]
然后选择具有更高后验概率的类作为输出。这里的 \(n\) 指字典的维数,需要先把 \(x\) 转换为统一长度的向量。
在之前的例子中,输入的每一维特征都是是二元的,其对应的分布是伯努利分布。而当特征是多元时,其对应的分布应该用多项式分布建模。
实际上,即便一些原始的输入数据是连续值,我们可以通过一个映射表将连续值映射为离散值,然后运用朴素贝叶斯方法进行建模:
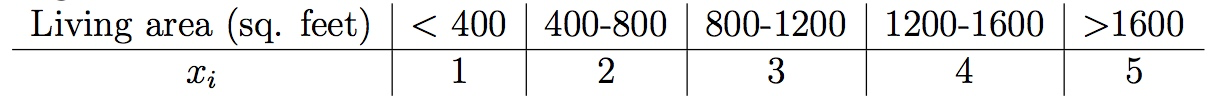
当原始连续值的数据不能很好的用多元正态分布进行建模时,将其离散化再使用朴素贝叶斯建模往往会取得更好的效果。
拉普拉斯平滑
朴素贝叶斯算法有很多的应用,但是其当前的形式仍存在一个问题:在垃圾邮件分类问题中,如果词典中存在一个词,而这个词在训练集中从未出现过时,其最大似然分析得出的参数 \(\phi_{35000|y}\) 将会是: \[ \begin{align*} \phi_{35000|y=1} &= \frac{\sum_{i=1}^m 1\{x_{35000}^{(i)}=1 \wedge y^{(i)}=1\}}{\sum_{i=1}^m 1\{y^{(i)}=1\}} =0 \\ \phi_{35000|y=0} &= \frac{\sum_{i=1}^m 1\{x_{35000}^{(i)}=1 \wedge y^{(i)}=0\}}{\sum_{i=1}^m 1\{y^{(i)}=0\}} = 0 \\ \end{align*} \]
因此,当我们尝试去预测含有该词的邮件是否为垃圾邮件时,后验概率的计算结果将变为: \[ \begin{align*} p(y=1 | x) &= \frac {(\prod_{i=1}^n p(x_i | y=1))p(y=1)}{(\prod_{i=1}^n p(x_i | y=1))p(y=1)+(\prod_{i=1}^n p(x_i | y=0))p(y=0)} \\ &= \frac 0 0 \end{align*} \]
这会导致我们无法进行预测。更一般的来看,如果你在有限的训练集上没有看到过某个事件,就认为其发生的概率为 0,这在统计学上是不合理的。
现在假设我们要分析一个多项式随机变量 \(z\) 的均值,取值为 \(\{1,\dots,k\}\),我们可以分析 \(\phi_j=p(z=j)\)。给定一个独立的观察集 \(\{z^{(1)},\dots,z^{(m)}\}\),最大似然估计的结果为:
\[ \phi_j = \frac {\sum_{i=1}^m 1\{z^{(i)}=j\}}{m} \]
如果我们用这个公式来进行最大似然估计,那么有一些 \(\phi_j\) 的值可能为0(如果未在观察集中出现)。为了避免这个问题,我们可以使用拉普拉斯平滑,其形式为: \[ \phi_j = \frac {\sum_{i=1}^m 1\{z^{(i)}=j\}+1}{m+k} \]
分子加 \(1\),分母加 \(k\),这样可以保证 \(\sum_{j=1}^m \phi_j=1\)(概率之和为1)。同时保证了对所有的取值, \(\phi_j \neq 0\),从而解决了之前的问题。实验证明,在大部分情况下,拉普拉斯平滑可以给出一个最优的估计。
对于朴素贝叶斯分类器,使用拉普拉斯平滑,可以得到如下公式: \[ \begin{align*} \phi_{j|y=1} &= \frac{\sum_{i=1}^m 1\{x_j^{(i)}=1 \wedge y^{(i)}=1\}+1}{\sum_{i=1}^m 1\{y^{(i)}=1\}+2}\\ \phi_{j|y=0} &= \frac{\sum_{i=1}^m 1\{x_j^{(i)}=1 \wedge y^{(i)}=0\}+1}{\sum_{i=1}^m 1\{y^{(i)}=0\}+2} \end{align*} \]
因为 \(x\) 的取值有两种,所以分子加 \(1\),分母加 \(2\)。在实际应用中,一般不需要对 \(\phi_y\) 进行拉普拉斯平滑。
文本分类的事件模型
让我们再探讨一个专门用于文本分类的模型来结束生成学习算法。虽然朴素贝叶斯对许多分类问题有很好的效果,但是对于文本分类,还存在着一个效果更棒的相关模型。
在文本分类领域,之前我们使用的朴素贝叶斯模型被称为多元伯努利事件模型。现在我们将使用一个不同的模型,叫作多项式事件模型。我们将使用与之前不同的方式来表示一封邮件:
令 \(x_i\) 表示邮件中的第 \(i\) 个词语,则其取值范围为 \(\{1,\ldots,|V|\}\),\(|V|\) 是词表(词典)的大小。一封含有 \(n\) 个词语的邮件现在将被表示为一个长度为 \(n\) 的向量 \((x_1,x_2,\ldots,x_n)\) ,注意 \(n\) 会随邮件的不同而变化。
该模型的参数为: \[ \begin{align*} \phi_{i|y=1} &= p(x_j = i | y=1)\\ \phi_{i|y=0} &= p(x_j = i | y=0)\\ \phi_y &= p(y) \end{align*} \]
我们假设 $p(x_j| y) $ 对所有的 \(j\)(邮件中词语的位置)都是一样的。
如果给定一个训练集 \(\{(x^{(i)},y^{(i)}); i=1,\ldots,m\}\),其中 \(x^{(i)} = (x_1^{(i)},x_2^{(i)},\dots,x_{n_i}^{(i)})\)。这里 \(n_i\) 表示第 \(i\) 个训练样本的词数,那么数据的似然函数可以表示为:
\[ \begin{align*} \mathcal{L} (\phi_y,\phi_{i|y=0},\phi_{i|y=1}) &= \prod_{i=1}^m p(x^{(i)},y^{(i)}) \\ &= \prod_{i=1}^m \left(\prod_{j=1}^{n_i} p(x_j^{(i)}\mid y;\phi_{i|y=0},\phi_{i|y=1}) \right) p(y^{(i)};\phi_y) \end{align*} \] 最大似然估计得出的结果如下: \[ \begin{align*} \phi_{k|y=1} &= \frac{\sum_{i=1}^m\sum_{j=1}^{n_i}1\{x_j^{(i)}=k \wedge y^{(i)}=1\}}{\sum_{i=1}^m 1\{y^{(i)}=1\}n_i} \\ \phi_{k|y=0} &= \frac{\sum_{i=1}^m\sum_{j=1}^{n_i} 1\{x_j^{(i)}=k \wedge y^{(i)}=0\}}{\sum_{i=1}^m 1\{y^{(i)}=0\}n_i} \\ \phi_y &= \frac {\sum_{i=1}^m 1\{y^{(i)} = 1\}}{m} \end{align*} \]
可以看到,这里在考虑字典中索引为 \(k\) 的词时,会把在每个文本中出现的次数相加。所以该模型相比于之前的模型,不仅仅考虑是否出现,还考虑了出现的次数。
如果要应用拉普拉斯平滑,可以在分子加 \(1\),分母加 \(|V|\),得到: \[ \begin{align*} \phi_{k|y=1} &= \frac{\sum_{i=1}^m\sum_{j=1}^{n_i}1\{x_j^{(i)}=k \wedge y^{(i)}=1\}+1}{\sum_{i=1}^m 1\{y^{(i)}=1\}n_i+|V|} \\ \phi_{k|y=0} &= \frac{\sum_{i=1}^m\sum_{j=1}^{n_i} 1\{x_j^{(i)}=k \wedge y^{(i)}=0\}+1}{\sum_{i=1}^m 1\{y^{(i)}=0\}n_i+|V|} \end{align*} \] 虽然朴素贝叶斯不是最好的分类算法,但因为其易于实现,所以非常适合作为你的第一个尝试。
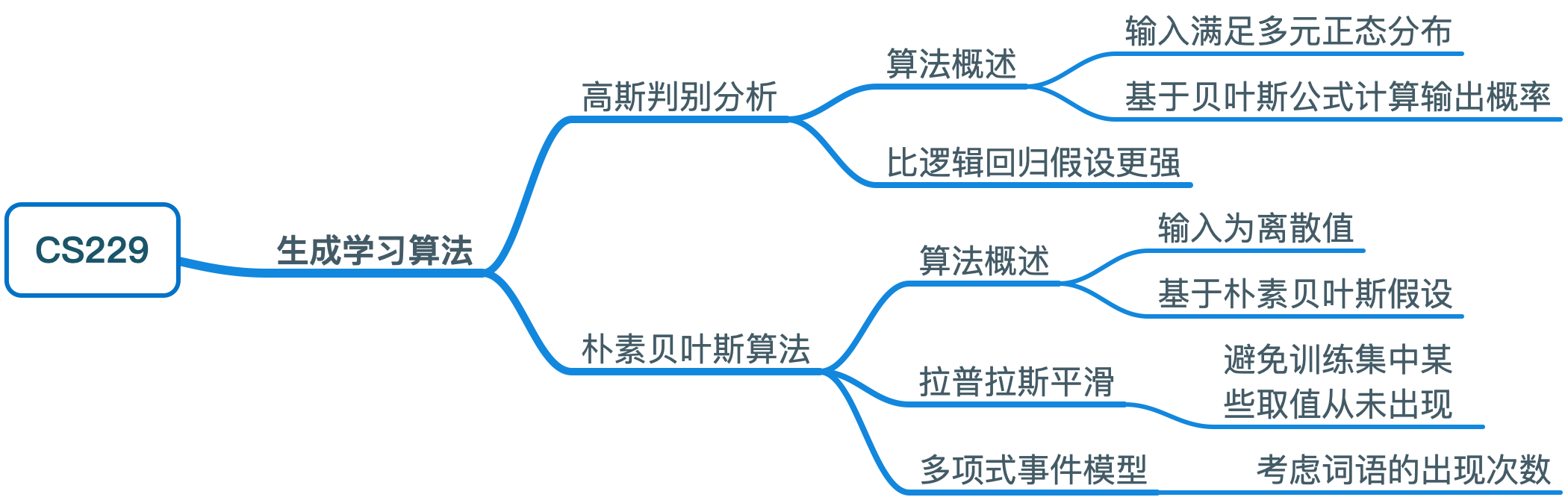
思维导图