CS229 学习笔记之九:聚类问题与 EM 算法
本篇博客为 CS229 学习笔记第九部分,主题是:聚类问题与 EM 算法。
K-means聚类
聚类问题是一种无监督学习,给定训练集 \(\{x^{(1)}, \ldots, x^{(m)}\}\),我们希望将其聚合成几个特定的类。k-means 聚类算法的流程如下:
- 随机初始化聚类中心 \(\mu_1,\mu_2,\dots, \mu_k \in \mathbb{R}^n\)
- 重复以下步骤直至收敛: 对于每个 \(i\)(训练集大小),令 \[ c^{(i)} := \arg \min_j ||x^{(i)}-\mu_j||^2 \] 对于每个 \(j\)(聚类数量),令 \[ \mu^{(j)} := \frac {\sum _{i=1}^m 1\{c^{(i)}=j\}x^{(i)}} {\sum _{i=1}^m 1\{c^{(i)}=j\}} \]
该算法的思想为:先将每个训练样本 \(x^{(i)}\) 分配到距离其最近的中心 \(\mu_j\),再将每个聚类中心移动到第一步中分配到该中心的样本的均值。
下图可视化了 k-means 算法的运行流程:
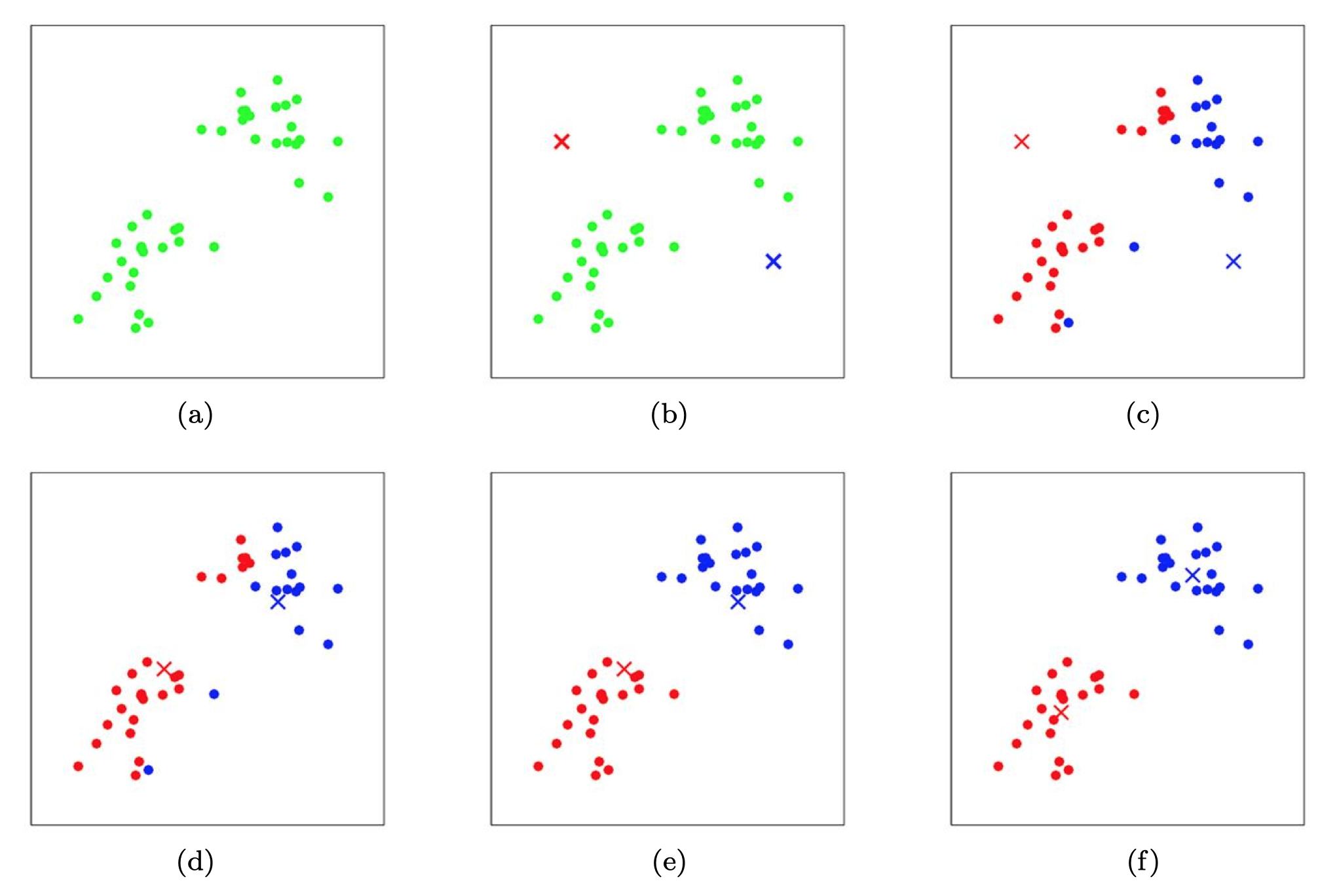
为了证明 k-means 算法能否保证收敛,我们定义失真函数(distortion function)为: \[ J(c,\mu) = \sum_{i=1}^m ||x^{(i)}-\mu_{c^{(i)}}||^2 \]
可以发现 k-means 本质上就是对失真函数进行坐标上升法优化:其内层循环首先保持 \(\mu\) 不变关于 \(c\) 最小化 \(J\),然后保持 \(c\) 不变关于 \(\mu\) 最小化 \(J\)。因此,\(J\) 一定会持续下降,最终达到收敛。一般 \(c\) 和 \(\mu\) 也会收敛,但理论上存在同时出现多种聚类组合的可能性,使得失真函数的值一样。
失真函数是一个非凸函数,这意味着坐标上升并不能保证其收敛至全局最优,存在收敛到局部最优的可能性。一般情况下这不会发生,可以通过多次运行 k-means 算法,选择最优解来解决这个问题。
混合高斯分布
混合高斯分布可以用于软聚类问题,即输出一个样本属于各个类的概率。我们可以将数据的类别看作一个隐含随机变量 \(z\),并给出如下假设:
- \(z\) 服从多项式分布 \(z^{(i)} \sim \text{Multinomial}(\phi)\)
- 给定不同的 \(z\) ,\(x\) 服从不同的高斯分布 \(x^{(i)} | z^{(i)} = j \sim \mathcal{N}(\mu_i, \Sigma_j)\)
使用极大似然法求解该优化问题,可以得到如下的似然函数: \[ \begin{aligned} \ell(\phi,\mu,\Sigma) &= \sum_{i=1}^m \log p(x^{(i)};\phi,\mu,\Sigma) \\ &= \sum_{i=1}^m \log \sum_{z^{(i)} = 1}^k p(x^{(i)}| z^{(i)};\mu, \Sigma)p(z^{(i)};\phi) \end{aligned} \] 该问题无法求出闭合解。如果 \(z^{(i)}\) 已知,即我们知道每个样本来自于哪个高斯分布,那么极大似然估计的求解是容易的,似然函数如下: \[ \ell(\phi,\mu,\Sigma) = \sum_{i=1}^m \left(\log p(x^{(i)}| z^{(i)};\mu, \Sigma)+ \log p(z^{(i)};\phi)\right) \]
求解的结果是: \[ \begin{aligned} \phi_j &= \frac 1 m \sum_{i=1}^m 1\{z^{(i)} = j\} \\ \mu_j &= \frac{\sum_{i=1}^m 1\{z^{(i)}=j\}x^{(i)}}{\sum_{i=1}^m 1\{z^{(i)}=j\}} \\ \Sigma_j &= \frac{\sum_{i=1}^m 1\{z^{(i)}=j\}(x^{(i)}-\mu_{j})(x^{(i)}-\mu_{j})^T}{\sum_{i=1}^m 1\{z^{(i)}=j\}} \end{aligned} \]
该结果与之前的高斯判别分析的结论类似(GDA 的协方差矩阵必须相同)。
EM 算法初步
实际上,我们并不知道 \(z^{(i)}\) 的值。我们可以通过 EM 算法进行迭代估计出 \(z^{i}\) 从而得到参数,其基本思想如下:
重复以下步骤直至收敛:
E-step对于每个 \(i,j\),令: \[ w_j^{(i)} := p(z^{(i)} = j|x^{(i)};\phi,\mu,\Sigma) \]
M-step更新参数: \[ \begin{aligned} \phi_j &= \frac 1 m \sum_{i=1}^m w_j^{(i)} \\ \mu_j &= \frac{\sum_{i=1}^m w_j^{(i)}x^{(i)}}{\sum_{i=1}^m w_j^{(i)}} \\ \Sigma_j &= \frac{\sum_{i=1}^m w_j^{(i)}(x^{(i)}-\mu_{j})(x^{(i)}-\mu_{j})^T}{\sum_{i=1}^m w_j^{(i)}} \end{aligned} \]
关于 EM 算法的几点解释:
在 E-step 中,给定 \(x^{(i)}\),我们使用当前的参数值来计算 \(z^{(i)}\) 的后验概率,即 \[ p(z^{(i)} = j|x^{(i)};\phi,\mu,\Sigma) = \frac {p(x^{(i)}|z^{(i)} = j;\mu,\Sigma)p(z^{(i)}=j;\phi)} {\sum_{l=1}^k p(x^{(i)}|z^{(i)}=l;\mu,\Sigma)p(z^{(i)}=l;\phi)} \]
该概率代表我们对 \(z^{(i)}\) 值的软猜测(即以概率值代替具体的值)。
在 M-step 中,参数的更新公式与之前已知 \(z^{(i)}\) 的公式相比,只是把指示函数替换为了概率。
与 K-means 算法相比,EM 算法输出的是样本属于各个类的概率,这是一种软聚类。与 K-means 相似,EM 算法容易陷入局部最优,因此多次尝试不同的初始参数可能是一个好主意。下两节将给出 EM 算法的一般形式,并证明其收敛性。
Jensen 不等式
本节将介绍 Jensen 不等式,其在 EM 算法中有着重要的作用。
函数的凹凸性
在介绍 Jensen 不等式之前,先简单回顾一下函数的凹凸性。对于一个实数域的函数 \(f\),其为凸函数的条件为 \(f''(x) \ge 0\)。如果输入为向量形式,则该条件可推广为其 Hessian 矩阵半正定(\(H \ge 0\))。
如果 \(f''(x) > 0\)(\(H > 0\)),则函数严格凸。凹函数的判定条件与凸函数完全相反。
定理
令 \(f\) 是一个凸函数,\(X\) 是一个随机变量,则: \[ \text{E}[f(X)] \ge f(\text{E}X) \]
如果 \(f\) 严格凸,那么当且仅当 \(X = \text{E}[X]\) 时等号成立(即 \(X\) 为常量)。可以通过下图对该不等式有一个直观的理解:
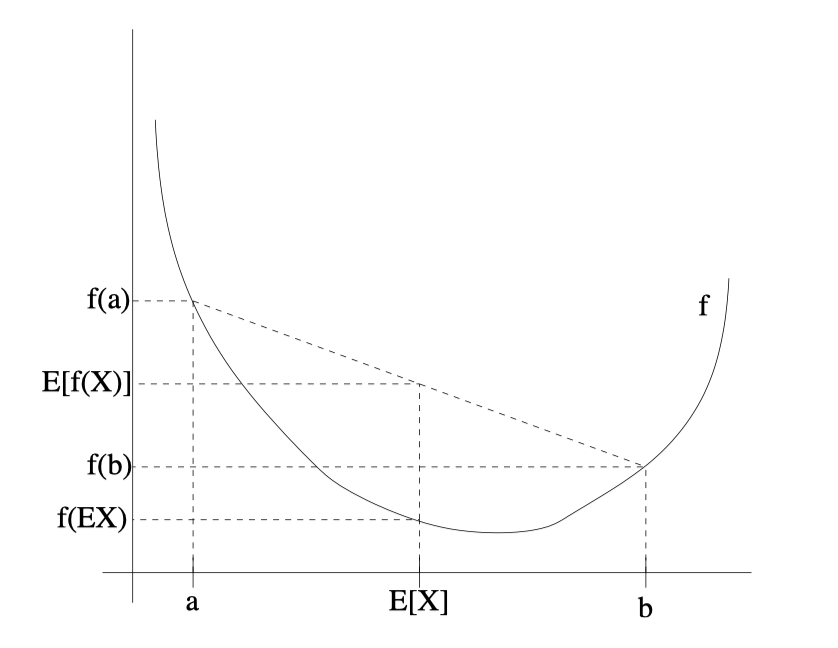
当 \(f\) 为凹函数时,不等式方向对调,仍然成立。
EM 算法
算法的导出
假定我们有一个包含 m 个独立样本的训练集,我们希望去拟合一个概率模型 \(p(x,z)\),其对数似然函数为: \[ \begin{aligned} \ell(\theta) &= \sum_{i=1}^m \log p(x;\theta) \\ &= \sum_{i=1}^m \log \sum_z p(x,z;\theta) \end{aligned} \]
这里假定 \(z\) 是离散变量(连续变量需要使用积分)。
直接最大化 \(\ell(\theta)\) 是难以求解的。EM 算法的思想是先构建一个 \(\ell\) 的下界(E-step),然后去优化这个下界(M-step),达到间接最大化 \(\ell\) 的目的。
对于每个 \(i\),设 \(Q_i\) 是 \(z\) 的某种概率分布(\(\sum_z Q_i(z) = 1, Q_i(z) \ge 0\))。根据期望的定义以及 Jensen 不等式,我们有: \[ \begin{align*} \sum_i \log p(x^{(i)};\theta) &= \sum_i \log \sum_{z^{(i)}} p(x^{(i)},z^{(i)};\theta) \tag{1} \\ &= \sum_i \log \sum_{z^{(i)}} Q_i(z^{(i)}) \frac {p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})} \tag{2} \\ &\ge \sum_i \sum_{z^{(i)}} Q_i(z^{(i)}) \log \frac {p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})} \tag{3} \\ \end{align*} \]
\(\frac {p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}\) 可以看做 \(z^{(i)}\) 的随机变量,其概率分布为 \(Q_i\),期望可以通过 \(\sum_{z^{(i)}} Q_i(z^{(i)}) \frac {p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}\) 得到。\(f(x) = \log x\) 是一个凹函数,应用 Jensen 不等式时注意方向对调。
为了执行 EM 算法,我们需要选择合适的 \(Q_i\) 以保证在当前的参数设置下取到下界,即目前的 \(\theta\) 值能够使得 (3) 式的等号成立。之前的定理表明等号成立的条件是随机变量为常数:
\[ \frac {p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})} = c \]
因此只要 \(Q_i(z^{(i)})\) 和 \(p(x^{(i)},z^{(i)};\theta)\) 成比例即可: \[ Q_i(z^{(i)}) \propto p(x^{(i)},z^{(i)};\theta) \] 实际上,因为 \(\sum_z Q_i(z^{(i)}) = 1\),将其代入上述公式,可以得到: \[ \sum_z Q_i(z^{(i)}) = \frac {\sum_z p(x^{(i)},z^{(i)};\theta)} c = 1 \] 因此 \(c = \sum_z p(x^{(i)},z^{(i)};\theta)\),从而有: \[ \begin{aligned} Q_i(z^{(i)}) &= \frac {p(x^{(i)},z^{(i)};\theta)} {\sum_z p(x^{(i)},z^{(i)};\theta)} \\ &= \frac {p(x^{(i)},z^{(i)};\theta)} {p(x^{(i)};\theta)} \\ &= p(z^{(i)}|x^{(i)};\theta) \end{aligned} \] 根据上述推导,我们只需要将 \(Q_i\) 设置为给定 \(x^{(i)}\) 时 \(z^{(i)}\) 的后验分布即可(以 \(\theta\) 为参数)。
综上所述,EM 算法的具体步骤为:
- E-step:对于每个 \(i\),令 \[ Q_i(z^{(i)}) := p(z^{(i)}|x^{(i)};\theta) \]
- M-step:更新参数 \[ \theta := \arg \max_\theta \sum_i \sum_{z^{(i)}} Q_i(z^{(i)}) \log \frac {p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})} \]
重复以上两个步骤直至收敛。
收敛性证明
下面证明该算法的收敛性。假定 \(\theta^{(t)}\) 和 \(\theta^{(t+1)}\) 来自于 EM 算法的两次成功的迭代,那么通过证明 \(\ell(\theta^{(t)}) \le \ell(\theta^{(t+1)})\),就可以表明 EM 算法是单调收敛的(对数似然函数单调递增)。
当参数为 \(\theta^{(t)}\) 时,根据算法步骤,我们令 \(Q_i^{(t)}(z^{(i)}) := p(z^{(i)}|x^{(i)};\theta^{(t)})\),这一选择保证了等号成立,即: \[ \ell(\theta^{(t)}) = \sum_i \sum_{z^{(i)}} Q_i^{(t)}(z^{(i)}) \log \frac {p(x^{(i)},z^{(i)};\theta^{(t)})}{Q_i^{(t)}(z^{(i)})} \] 而参数 \(\theta^{(t+1)}\) 是通过最大化上式的右边部分得出的(更新 \(\theta\)),因此有: \[ \begin{align*} \ell(\theta^{(t+1)}) &\ge \sum_i \sum_{z^{(i)}} Q_i^{(t)}(z^{(i)}) \log \frac {p(x^{(i)},z^{(i)};\theta^{(t+1)})}{Q_i^{(t)}(z^{(i)})} \tag{4} \\ &\ge \sum_i \sum_{z^{(i)}} Q_i^{(t)}(z^{(i)}) \log \frac {p(x^{(i)},z^{(i)};\theta^{(t)})}{Q_i^{(t)}(z^{(i)})} \tag{5}\\ &= \ell(\theta^{(t)}) \tag{6} \end{align*} \]
- 式的得出来源于 (3) 式;(5) 式的得出来源于 \(\theta^{(t+1)}\) 是上一步的下界最大化的结果;(6) 式的得出之前已经证明(满足等号成立的条件)。
综上所述,EM 算法可以保证似然函数的单调收敛。一个可取的收敛条件是 \(\ell(\theta)\) 的增长速度小于某个临界值。
坐标上升法
如果我们定义: \[ J(Q,\theta) = \sum_i \sum_{z^{(i)}} Q_i(z^{(i)}) \log \frac {p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})} \]
从之前的推导可以知道 \(\ell(\theta) \ge J(Q,\theta)\)。
那么 EM 算法可以看做是对 \(J\) 的坐标上升法:
- 在 E-step 中,关于 \(Q\) 最大化 \(J\)(使等号成立)
- 在 M-step 中,关于 \(\theta\) 最大化 \(J\)
混合高斯模型复盘
下面将使用 EM 算法的一般形式来对之前混合高斯模型中的公式进行推导,由于篇幅所限,这里只给出 \(\phi\) 和 \(\mu_j\) 的推导过程。
之前我们得出的参数更新公式如下: \[ \begin{aligned} \phi_j &= \frac 1 m \sum_{i=1}^m w_j^{(i)} \\ \mu_j &= \frac{\sum_{i=1}^m w_j^{(i)}x^{(i)}}{\sum_{i=1}^m w_j^{(i)}} \\ \Sigma_j &= \frac{\sum_{i=1}^m w_j^{(i)}(x^{(i)}-\mu_{j})(x^{(i)}-\mu_{j})^T}{\sum_{i=1}^m w_j^{(i)}} \end{aligned} \] 根据 E-step 的定义,我们可以得到: \[ w_j^{(i)} = Q_i(z^{(i)} = j) = P(z^{(i)} = j|x^{(i)};\phi,\mu,\Sigma) \] 在 M-step 中,我们需要通过上述三个参数去最大化下式: \[ \begin{aligned} \sum_{i=1}^m &\sum_{z^{(i)}} Q_i(z^{(i)}) \log \frac {p(x^{(i)},z^{(i)};\phi,\mu,\Sigma)}{Q_i(z^{(i)})} \\ &= \sum_{i=1}^m\sum_{j=1}^k Q_i(z^{(i)}=j) \log \frac {p(x^{(i)}|z^{(i)}=j;\mu,\Sigma)p(z^{(i)}=j;\phi)}{Q_i(z^{(i)}=j)} \\ &= \sum_{i=1}^m\sum_{j=1}^k w_j^{(i)} \log \frac {\frac 1 {(2\pi)^{n/2}|\Sigma_j|^{1/2}}\exp \left(-\frac 1 2 (x^{(i)}-\mu_j)^T\Sigma_j^{-1}(x^{(i)}-\mu_j)\right)\cdot\phi_j}{w_j^{(i)}} \end{aligned} \] 我们首先关于 \(\mu_j\) 去进行最大化,求导可得: \[ \begin{aligned} \nabla_{\mu_j}&\sum_{i=1}^m\sum_{j=1}^k w_j^{(i)} \log \frac {\frac 1 {(2\pi)^{n/2}|\sum_j|^{1/2}}\exp \left(-\frac 1 2 (x^{(i)}-\mu_j)^T\Sigma_j^{-1}(x^{(i)}-\mu_j)\right)\cdot\phi_j}{w_j^{(i)}} \\ &= - \nabla_{\mu_j} \sum_{i=1}^m\sum_{j=1}^k w_j^{(i)}\frac 1 2 (x^{(i)}-\mu_j)^T\Sigma_j^{-1}(x^{(i)}-\mu_j) \\ &= \frac 1 2 \sum_{i=1}^m w_j^{(i)} \nabla_{\mu_j} 2\mu_j^T \Sigma_j^{-1}x^{(i)}-\mu_j^T\Sigma_j^{-1}\mu_j \\ &= \sum_{i=1}^m w_j^{(i)} (\Sigma_j^{-1}x^{(i)}-\Sigma_j^{-1}\mu_j) \end{aligned} \]
上述推导首先去除了不相关的项,然后去除了求和符号(只求当前的 \(j\) 的导数),最后合并同类项得到结果。将上式设为 0 求解 \(\mu_j\),可得: \[ \mu_j = \frac{\sum_{i=1}^m w_j^{(i)}x^{(i)}}{\sum_{i=1}^m w_j^{(i)}} \] 下面关于 \(\phi_j\) 去进行最大化,将与 \(\phi_j\) 相关的部分提取出来,可以得到需要最大化的项为: \[ \sum_{i=1}^m\sum_{j=1}^k w_j^{(i)}\log \phi_j \]
这里我们还有一个额外的约束条件:\(\sum_{j=1}^k\phi_j = 1\)
因此,我们需要构建拉格朗日算子: \[ \mathcal{L}(\phi) = \sum_{i=1}^m\sum_{j=1}^k w_j^{(i)}\log \phi_j + \beta (\sum_{j=1}^k \phi -1) \]
其中 \(\beta\) 是拉格朗日乘数,对上式求导可得: \[ \frac {\partial}{\partial\phi_j} \mathcal{L}(\phi) = \sum_{i=1}^m \frac{w_j^{(i)}}{\phi_j} + \beta \]
将其设为 0,可得: \[ \phi_j = \frac {\sum_{i=1}^m w_j^{(i)}} {-\beta} \] 由于 \(\sum_j \phi_j = 1\),因此 \(-\beta = \sum_{i=1}^m \sum_{j=1}^k w_j^{(i)} = \sum_{i=1}^m 1 = m\),所以: \[ \phi_j = \frac 1 m \sum_{i=1}^m w_j^{(i)} \]
思维导图
