CS229 学习笔记之十一：主成分分析

本篇博客为 CS229 学习笔记第十一部分，主题是：主成分分析。

引入

在上一章，我们介绍了因子分析，其给出了一种将 \(n\) 维数据 \(x\) 在 \(k\) 维子空间中建模的方法。其基于概率模型，通过 EM 算法来估计参数。

本章我们将介绍另一种降维方法：主成分分析法（PCA）。该方法更加直接，只需要特征向量的计算，不需要 EM 求解。

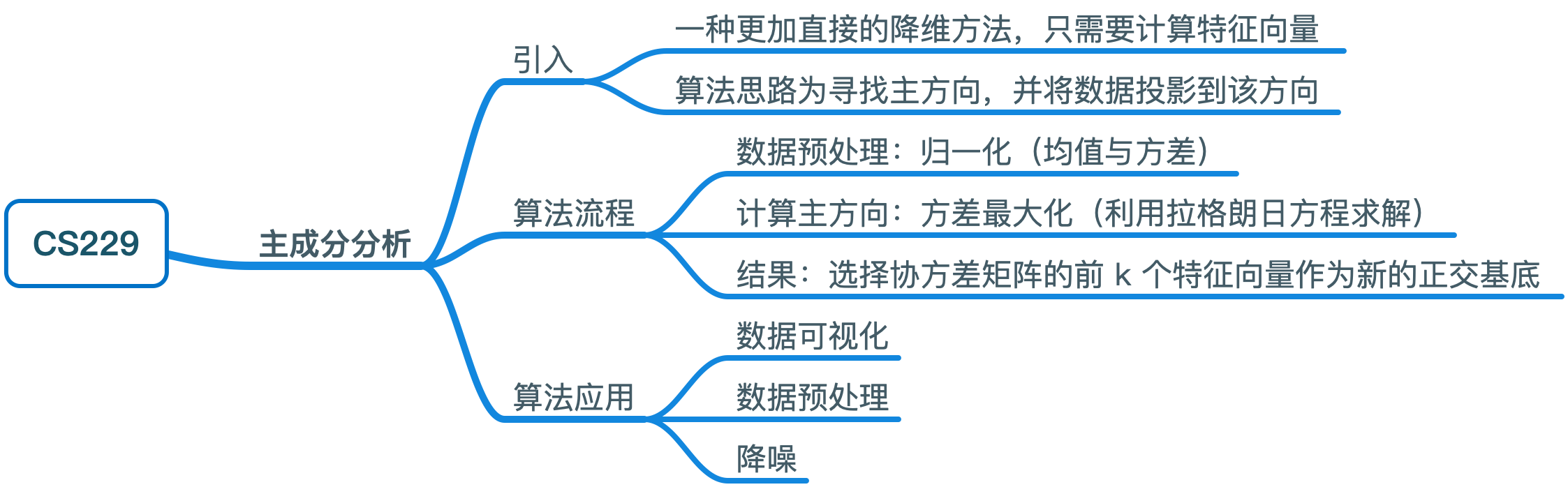
给定一个数据集 \(\{x^{(i)};i=1,\ldots,m\}\)，其中 \(x^{(i)} \in \mathbb{R}^n (n \ll m)\)。假定该数据集来自对无线电控制直升机飞行员的调查，而其中的两个属性分别为飞行员的技能评估和其对飞行的感兴趣长度。

考虑到飞行的特殊性，这两个属性是存在正相关关系的，即实际上数据的信息量是 n-1 维的。PCA 解决的就是如何将多余属性去除的问题。

将上述两个属性使用坐标图进行展示，得到：

可以看到，\(u1\) 展示出了数据之间的相关性，称之为“主方向”；\(u2\) 则代表主方向之外的噪声。PCA 要做的就是找到主方向，并将数据投影到该方向，达到降维的目的。

算法流程

预处理

在运行 PCA 算法之前，需要首先进行预处理来归一化数据均值及方差： 1. 令 \(\mu = \frac 1 m \sum_{i=1}^m x^{(i)}\) 2. 使用 \(x^{(i)} -\mu\) 来替代 \(x^{(i)}\) 3. 令 \(\sigma_j^2 = \frac 1 m \sum_i (x_j^{(i)})^2\) 4. 使用 \(x^{(i)}_j / \sigma_j\) 来替代 \(x^{(i)}\)

前两步将数据的均值变为 0（已知均值为 0 时可以省略）；后两步将数据每个维度的方差变为 1（已知数据各维度处于同一尺度下时可以省略）。

计算主方向

计算主方向的方法之一是找到单位向量 \(u\)，使得数据在该方向上的投影的方差最大化。

直观上来看，原始数据必然存在一定的方差（信息），而我们希望投影后的数据（降维后）在子空间尽量保留原始数据的信息，即方差最大化。

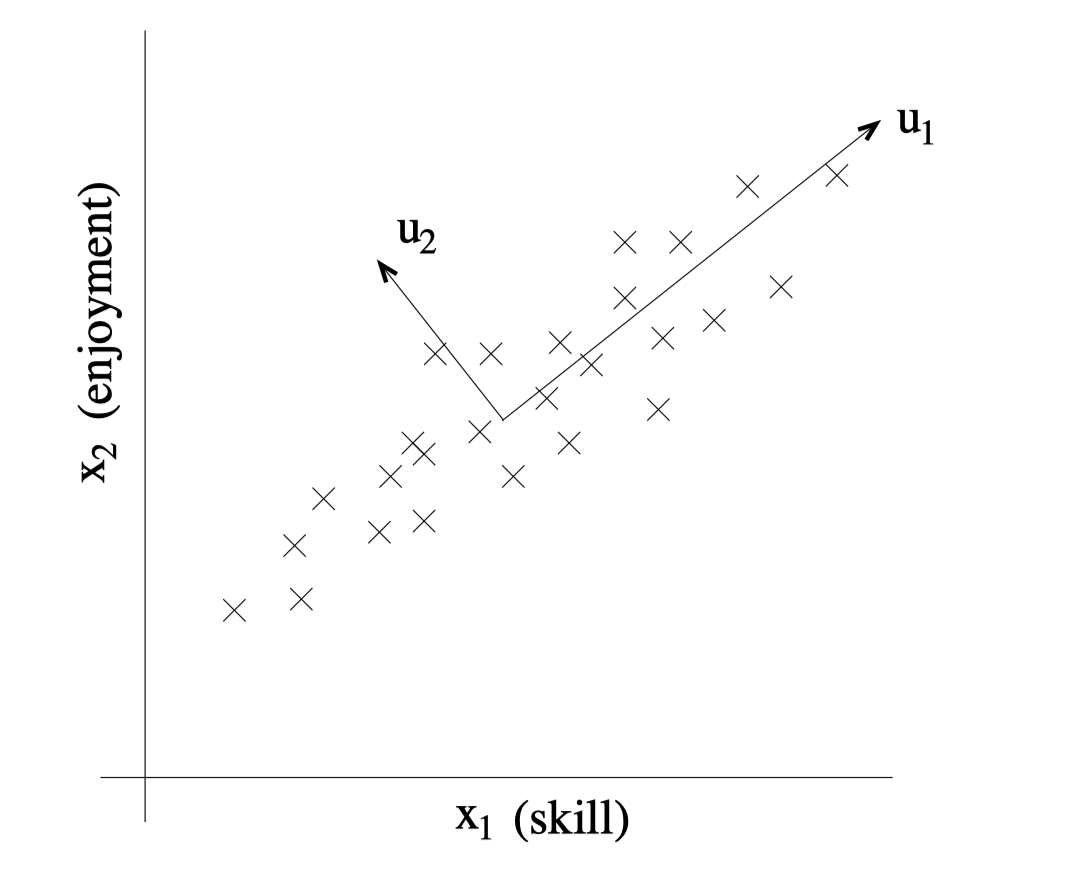
以如下数据集为例（归一化已完成）：

可以看到，图 2 方向上的投影相比图 3 距离原点更远，方差更大。我们希望能够自动找到类似图 2 的方向。

下面给出寻找该方向的方法：给定一个单位向量 \(u\) 和一个点 \(x\)，其投影长度（距离原点）为 \(x^Tu\)

因此，为了最大化投影的方差，即最大化： \[ \begin{aligned} \frac 1 m \sum_{i=1}^m (x^{(i)^T}u)^2 &= \frac 1 m \sum_{i=1}^m u^Tx^{(i)}x^{(i)^T}u \\ &= u^T\left(\frac 1 m \sum_{i=1}^m x^{(i)}x^{(i)^T}\right) u \end{aligned} \]

对于归一化后的数据，其投影点的均值也为 0，因此方差计算为直接平方。该公式有一个约束条件：\(||u||_2 =1\)。

利用拉格朗日方程，可以求得该最大化问题的解即为经验协方差矩阵 \(\Sigma = \frac 1 m \sum_{i=1}^m x^{(i)}x^{(i)^T}\) 的主要特征向量。构建如下拉格朗日方程： \[ \ell = u^T\Sigma u - \lambda(u^Tu-1) \] 对 \(u\) 求导，得到： \[ \begin{aligned} \nabla_u \ell &= \nabla_u u^T\Sigma u - \nabla_u u^Tu \\ &= \nabla_u \text{tr}(u^T\Sigma u) - \nabla_u \text{tr}(u^Tu) \\ &= \left(\nabla_{u^T} \text{tr}(u^T\Sigma u)\right)^T - \left(\nabla_{u^T} \text{tr}(u^Tu)\right)^T \\ &= (\Sigma u)^{T^T} - \lambda u^{T^T} \\ &= \Sigma u - \lambda u \end{aligned} \]

令导数为 0，得 \(\Sigma u = \lambda u\)，即 \(u\) 为 \(\Sigma\) 的特征向量，其特征值为 \(\lambda\)。

综上所述，如果我们需要将数据降至 1 维，则应该选择 \(\Sigma\) 的主要特征向量 \(u\) 作为主方向（特征值最大）

当需要将数据降为 k 维时（\(k < n\)），我们应该选择 \(\Sigma\) 的前 k 个特征向量 \(u_1, \ldots, u_k\) 作为主方向（因为 \(\Sigma\) 是对称矩阵，所以其可以得到 n 个相互正交的特征向量）。前 k 个即最大的 k 个特征值所对应的特征向量，这些特征向量形成了一个新的正交基底（k 维）。

基于该基底，可以将 \(x^{(i)}\) 进行降维： \[ y^{(i)} = \left[\begin{array}{cc} u_1^Tx^{(i)} \\ u_2^Tx^{(i)} \\ \vdots \\ u_k^Tx^{(i)} \end{array} \right] \in \mathbb{R}^k \]

向量 \(u_1, \ldots, u_k\) 被称为数据的前 k 个主成分。

算法应用

PCA 算法主要有如下三个应用方向：

• 数据可视化：将数据降至2-3维后进行可视化
• 数据预处理：在运行算法之前对数据进行降维，不仅能够提升计算速度，还能够降低假设的复杂性，避免过拟合；对线性分类器即意味着 VC 维的减小
• 降噪：去除数据中的无关干扰因素

总结

关于目前所学的降维与聚类方法可以总结为如下表格：

	密度估计（概率方法）	非概率方法
降维	因子分析	主成分分析
聚类	混合高斯模型	K 均值

思维导图