CS224N 学习笔记之一:词向量 1
本篇博客为 CS224N 学习笔记第一部分,主题是:词向量(简介,SVD 和 Word2Vec)。
自然语言处理简介
自然语言处理的特殊性
从处理的对象来看,NLP 与其他机器学习任务有很大区别:NLP 处理的对象是人类语言,而人类的语言是一种特定的用于传达意义的系统,并不由任何形式的物理表现产生,大部分词语只是一个表达某种意义的符号。语言通过各种方式编码(语音、手势、写作等),以连续信号的形式传输给大脑。
任务类型
NLP 的目标是设计算法来让计算机“理解”自然语言,以执行某些任务。这些任务可以划分为不同的难度等级,举例来说:
简单难度:
- 拼写检查
- 关键词搜索
- 同义词寻找
中等难度:
- 从网站、文档中解析信息
困难难度:
- 机器翻译
- 语义分析
- 指代消解
- 智能问答
如何表示词语
所有 NLP 任务的第一个议题就是如何表示词语以将其作为模型的输入。当前常见的做法是使用词向量来表示词语,下面将对各种不同的词向量技术进行介绍。
传统词向量
最简单的词向量表示方法是 one-hot 向量,其步骤如下:
构建一个大小为 \(|V|\) 的词典(如果是表示所有英语词汇,则大小约为 1300 万)
将每个词语表示为一个 \(\mathbb{R}^{|V|\times 1}\) 的向量。该词语在词典中的位置所对应的分量为 1 ,其他分量均为 0:
\[ w^{aardvark} = \left[\begin{array}{cc} 1 \\ 0 \\ 0 \\ \vdots \\ 0 \end{array}\right], w^{a} = \left[\begin{array}{cc} 0 \\ 1 \\ 0 \\ \vdots \\ 0 \end{array}\right], \cdots w^{zebra} = \left[\begin{array}{cc} 0 \\ 0 \\ 0 \\ \vdots \\ 1 \end{array}\right] \]
这种表示方法的缺陷是无法体现出词语之间的相关性: \[ (w^{hotel})^Tw^{motel} = (w^{hotel})^Tw^{cat} = 0 \]
我们希望减少向量空间的大小,找到一个能够表示词语间相关性的子空间。
基于 SVD 的方法
我们可以利用奇异值分解来减小向量空间的大小,具体步骤如下: 1. 基于数据集构建关于词语共现次数的某种矩阵 \(X\) 2. 对 \(X\) 进行奇异值分解得到 \(USV^T\) 3. 使用 \(U\) 的某些行来表示词向量
下面介绍两种可以选择的共现矩阵:
词语-文档矩阵
词语-文档矩阵假定相关的词语一般出现在相同的文档中,其构建步骤如下:
- 遍历所有文档(数量为 \(M\))
- 每一次词语 \(i\) 出现在文档 \(j\) ,\(X_{ij}\) 加 1
该矩阵的大小为 \(\mathbb{R}^{|V|\times M}\)。这是一个非常大的矩阵,计算过于复杂。
基于窗口的共现矩阵
基于窗口的共现矩阵计算每个词语在给定词语的特定大小窗口范围内出现的次数,矩阵的大小为 \(|V| \times |V|\)。
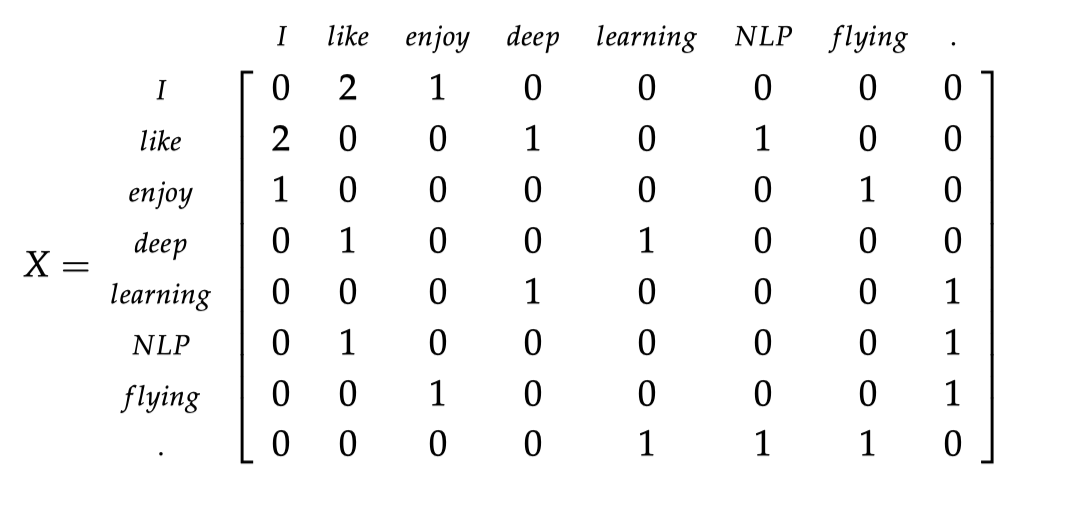
下面给出一个例子:该语料库由 3 个句子组成,且窗口大小设置为 1: 1. I enjoy flying. 2. I like NLP. 3. I like deep learning.
按上述方法得到的矩阵为:
将 SVD 应用到共现矩阵
观察 SVD 得到的奇异值( \(S\) 矩阵的对角线),按照所占的百分比选择适当的 \(k\): \[ \frac {\sum_{i=1}^k \sigma_i} {\sum_{i=1}^{|V|} \sigma_i} \] 然后选择矩阵 \(U\) 的前 \(k\) 行作为词向量,词向量的长度为 \(k\)。该向量能够表示词语的语法和语义信息。
下面两张图给出了 SVD 的求解过程:
使用 SVD 分解共现矩阵:
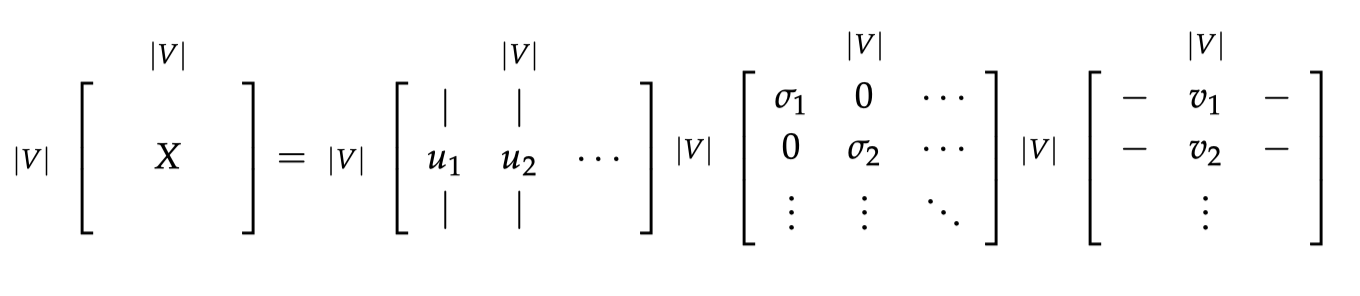
通过选择前 k 个奇异向量减少维度:
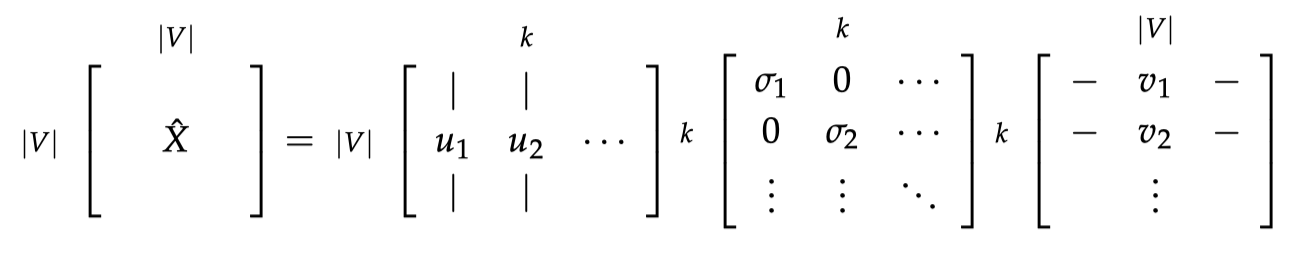
存在的问题
基于 SVD 的方法虽然减小了维数,但是存在很多的问题: + 矩阵维数经常变化(随语料库变化) + 矩阵非常稀疏(因为大部分词语不存在共现) + 矩阵维数一般非常高(\(\approx 10^6 \times 10^6\)) + 计算复杂度是平方级的(执行 SVD) + 需要一些技巧来处理词语频率间的极度不平衡
针对上述问题,可以采取如下的解决方案: + 忽略一些功能性词语(如 the、he、has 等) + 使用一个有坡度的窗口(即基于词语之间的距离设置不同的共现权重) + 使用皮尔逊相关性(中心化的余弦相似度)替代原始计数,并将负数置为 0
接下来,我们会介绍一种能更优雅地解决上述诸多问题的方案:基于迭代的方法。
基于迭代的方法:Word2vec
基于迭代的方法通过迭代逐渐学习词语的共现关系,而非基于 SVD 的方法那样一次性直接获取所有词语的共现关系。训练的过程是:设置一个目标函数,基于某种更新规则进行迭代,不断优化目标函数,最终学习得到词向量。
本节将介绍其中一种方法:Word2vec。Word2vec 是一个软件包,实际包括:
两种算法:CBOW 和 skip-gram
- CBOW 的目标是基于上下文预测中心词
- Skip-gram 的目标是基于中心词预测上下文
两种训练方法:negative sampling 和 hierarchical softmax
- negative sampling 通过采集负样本定义目标函数
- hierarchical softmax 通过一个高效的树结构计算所有词语的概率来定义目标函数
语言模型
word2vec 可以理解为是语言模型的副产物,语言模型用于计算一个词语序列的概率。如果这个序列是合理的(语义和语法上),其概率就会比较高,否则输出的概率就会比较低。该概率用数学公式可以表示为:
\[ P(w_1,w_2,\ldots,w_n) \] 如果将每个词语的出现看作完全独立,就可以得到 Unigram model: \[ P(w_1,w_2,\ldots,w_n) = \prod_{i=1}^n P(w_i) \] 如果假设每个词语的出现于其前一个词语相关,就可以得到 Bigram model: \[ P(w_1,w_2,\ldots,w_n) = \prod_{i=2}^n P(w_i|w_{i-1}) \] 上述两种模型都过于理想化,实际情况下一个词语的出现概率受到更多因素的影响。下面将介绍如何通过模型学习这些概率。
CBOW
第一种方法是给定一个单词的上下文,来预测或生成该单词,该模型称为连续词袋模型(CBOW)。
符号定义
为了具体描述 CBOW,需要明确以下定义: + \(w_i\):来自词典 \(V\) 的词语 \(i\) + \(\mathcal{V} \in \mathbb{R}^{n\times |V|}\):输入词语矩阵 + \(n\) 是我们希望的词向量(嵌入)空间大小 + \(v_i\):\(\mathcal{V}\) 的第 \(i\) 列,词语 \(w_i\) 的输入向量表示 + \(\mathcal{U} \in \mathbb{R}^{|V|\times n}\):输出词语矩阵 + \(u_i\):\(\mathcal{U}\) 的第 \(i\) 行,词语 \(w_i\) 的输出向量表示
CBOW 的目的是学习得到每一个词语 \(w_i\) 的输入向量 \(v_i\) 和输出向量 \(u_i\).
计算步骤
CBOW 的具体步骤如下:
基于输入上下文(大小为 m)生成 one-hot 词语向量: \[ x^{(c-m)},\ldots,x^{(c-1)},x^{(c+1)},\dots,x^{(c+m)} \in \mathbb{R}^{|V|} \]
与输入词语矩阵相乘,得到上下文嵌入词向量: \[ v_{c-m} = \mathcal{V}x^{(c-m)},v_{c-m+1} = \mathcal{V}x^{(c-m+1)},\ldots,v_{c+m} = \mathcal{V}x^{(c+m)} \in \mathbb{R}^n \]
- 由于 one-hot 向量的性质,得到的词向量即为 \(\mathcal{V}\) 的每一列
将这些向量进行平均: \[ \hat{v} = \frac {v_{c-m}+v_{c-m+1}+\ldots+v_{c+m}} {2m} \in \mathbb{R}^n \]
- 可以理解为用该平均向量表示待预测的词语
生成一个得分向量: \[ z = \mathcal{U}\hat{v} \in \mathbb{R}^{|V|} \]
- 因为相似的向量的点积更大,所以该得分向量可以反映出每个词语与待预测词语的相似程度
使用 softmax 将得分转换为概率: \[ \hat{y} = \text{softmax}(z) \in \mathbb{R}^{|V|} \]
- softmax 的具体形式为 \(\frac {e^{z_i}} {\sum_{k=1}^{|V|} e^{z_k}}\)
我们希望生成的概率 \(\hat{y} \in \mathbb{R}^{|V|}\) 能够匹配真实的概率 \(y \in \mathbb{R}^{|V|}\)
- 该真实概率实际上就是一个 one-hot 向量(对应到待预测的中心词)
学习方法
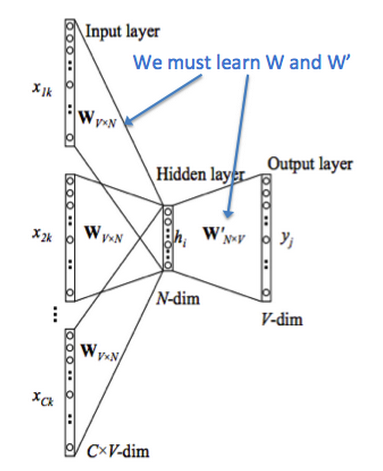
了解到模型的计算方法后,我们希望学习得到 \(\mathcal{V}\) 和 \(\mathcal{U}\)。我们需要构建一个目标函数来进行优化,这里选择交叉熵函数 \(H(\hat{y},y)\):
\[ H(\hat{y},y) = - \sum_{j=1}^{|V|} y_j \log(\hat{y_j}) \] 由于 \(y\) 是一个 one-hot 向量,所以实际的代价函数可以简化为: \[ H(\hat{y},y) = -y_c \log(\hat{y}_c) \]
其中 \(c\) 是中心词的位置(one-hot 向量分量为 1)。因此,综合上述公式,可以得到待优化的目标函数为: \[ \begin{aligned} \text{minimize}\;J &= -\log P(w_c | w_{c-m},\ldots, w_{c-1},w_{c+1},\ldots,w_{c+m}) \\ &= -\log P(u_c | \hat{v}) \\ &= -\log \frac {\exp(u_c^T\hat{v})} {\sum_{j=1}^{|V|} \exp(u_j^T\hat{v})} \\ &= -u_c^T\hat{v} + \log \sum_{j=1}^{|V|} \exp(u_j^T\hat{v}) \end{aligned} \]
我们可以使用随机梯度下降来更新所有相关的词向量 \(u_c\) 和 \(\hat{v}\): \[ \mathcal{U}_{new} \leftarrow \mathcal{U}_{old} -\alpha \nabla_{\mathcal{U}} J \\ \mathcal{V}_{new} \leftarrow \mathcal{V}_{old} -\alpha \nabla_{\mathcal{V}} J \]
Skip-Gram
另一种方法是给定一个中心词,去预测或生成周围的词语,该模型被称为 Skim-Gram 模型。
符号定义
Skim-Gram 模型的定义与 CBOW 基本相同,只是输入输出对调: - \(w_i\):来自词典 \(V\) 的词语 \(i\) - \(\mathcal{V} \in \mathbb{R}^{n\times |V|}\):输入词语矩阵 - \(n\) 是我们希望的词向量(嵌入)空间大小 - \(v_i\):\(\mathcal{V}\) 的第 \(i\) 列,词语 \(w_i\) 的输入向量表示 - \(\mathcal{U} \in \mathbb{R}^{|V|\times n}\):输出词语矩阵 - \(u_i\):\(\mathcal{U}\) 的第 \(i\) 行,词语 \(w_i\) 的输出向量表示
计算步骤
Skip-Gram 的具体步骤如下:
生成关于中心词的 one-hot 向量作为输入 \(x \in \mathbb{R}^{|V|}\)
与输入词语矩阵相乘,得到中心词的嵌入词向量: \[ v_c = \mathcal{V}x \in \mathbb{R}^{n} \]
生成一个得分向量: \[ z = \mathcal{U}v_c \in \mathbb{R}^{|V|} \]
将得分向量转换为概率: \[ \hat{y} = \text{softmax}(z) \in \mathbb{R}^{|V|} \]
- 其中 \(\hat{y}_{c-m},\ldots, \hat{y}_{c-1},\hat{y}_{c+1},\ldots,\hat{y}_{c+m}\) 对应为该中心词的周围词语的概率
我们希望生成的概率与真实的概率 \(y^{(c-m)},\ldots, y^{(c-1)},y^{(c+1)},\ldots,y^{(c+m)}\) 匹配(one-hot 向量)
学习方法
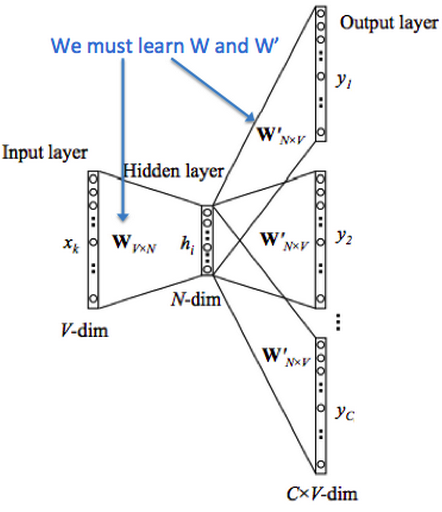
在构建 skip-gram 模型的目标函数时,使用了贝叶斯假设(即条件独立假设):给定中心词的情况下,所有输出词语都完全独立。因此,代价函数如下:
\[ \begin{aligned} \text{minimize}\;J &= -\log P( w_{c-m},\ldots, w_{c-1},w_{c+1},\ldots,w_{c+m} | w_c ) \\ &= -\log \prod_{j=0,j \ne m}^{2m} P(w_{c-m+j} | w_c) \\ &= -\log \prod_{j=0,j \ne m}^{2m} P(u_{c-m+j} | v_c) \\ &= -\log \prod_{j=0,j \ne m}^{2m} \frac {\exp(u_{c-m+j}^Tv_c)} {\sum_{k=1}^{|V|} \exp(u_k^Tv_c)} \\ &= - \sum_{j=0,j \ne m}^{2m} u_{c-m+j}^Tv_c + 2m \log \sum_{k=1}^{|V|} \exp(u_k^Tv_c) \end{aligned} \] 基于上述代价函数,可以通过随机梯度下降更新参数。
注意:代价函数还可以写成如下形式: \[ \begin{aligned} J &= - \sum_{j=0,j \ne m}^{2m} \log P(u_{c-m+j}|v_c) \\ &= \sum_{j=0,j \ne m}^{2m} H(\hat{y},y_{c-m+j}) \end{aligned} \]
- 其中 \(H(\hat{y},y_{c-m+j})\) 是概率向量 \(\hat{y}\) 和 one-hot 向量 \(y_{c-m+j}\) 的交叉熵
Negative Sampling
对于上述的两种模型,其代价函数需要在 \(|V|\) 上进行累加,其时间复杂度为 \(O(|V|)\)。为了减少计算复杂度,在每一次迭代中,我们可以仅对部分负样本进行采样,采样基于一个噪声分布 \(P_n(w)\) 进行,其概率与词典中词频顺序匹配。Gensim 默认使用 CBOW 和负采样。
新的目标函数
实际上,负采样在优化一个不同的目标函数。考虑一个由一个词语和一个上下文组成的单词对:\((w,c)\),现在我们考虑的是该单词对是否出自训练数据:
- 定义 \(P(D=1|w,c)\) 为 \((w,c)\) 出自语料库的概率
- 定义 \(P(D=0|w,c)\) 为 \((w,c)\) 不出自语料库的概率
我们使用 sigmoid 函数来定义 \(P(D=1|w,c)\),sigmoid 可以理解为 1 维版本的 softmax 函数: \[ P(D=1|w,c) = \sigma(u_w^Tv_c) = \frac 1 {1+e^{(-u_w^Tv_c)}} \]
新的目标函数希望最大化上述两个概率:当单词对实际上出自语料库时,最大化 \(P(D=1|w,c)\);当单词对实际上并不出自语料库时,最大化 \(P(D=0|w,c)\),具体公式如下:
\[ \begin{aligned} \theta &= \arg\max_\theta \prod_{(w,c)\in D} P(D=1|w,c,\theta) \prod_{(w,c)\in \tilde{D}} P(D=0|w,c,\theta) \\ &= \arg\max_\theta \prod_{(w,c)\in D} P(D=1|w,c,\theta) \prod_{(w,c)\in \tilde{D}} (1-P(D=1|w,c,\theta)) \\ &= \arg\max_\theta \sum_{(w,c)\in D} \log P(D=1|w,c,\theta) + \sum_{(w,c)\in \tilde{D}} \log (1-P(D=1|w,c,\theta)) \\ &= \arg\max_\theta \sum_{(w,c)\in D} \log \frac 1 {1+\exp(-u_w^Tv_c)} + \sum_{(w,c)\in \tilde{D}} \log (1- \frac 1 {1+\exp(-u_w^Tv_c)}) \\ &= \arg\max_\theta \sum_{(w,c)\in D} \log \frac 1 {1+\exp(-u_w^Tv_c)} + \sum_{(w,c)\in \tilde{D}} \log (\frac 1 {1+\exp(u_w^Tv_c)}) \\ \end{aligned} \]
- 公式中使用 \(\theta\) 表示模型的参数,实际上参数为 \(\mathcal{V}\) 和 \(\mathcal{U}\)
最大化似然函数与最小化负的似然函数等价,因此可以得到如下代价函数: \[ J = - \sum_{(w,c)\in D} \log \frac 1 {1+\exp(-u_w^Tv_c)} - \sum_{(w,c)\in \tilde{D}} \log (\frac 1 {1+\exp(u_w^Tv_c)}) \]
其中 \(\tilde{D}\) 指负语料库,即在实际情况中不太可能出现的句子,一般我们使用基于某个噪声分布随机采样的方式生成 \(\tilde{D}\)。
对两种模型的改进
对于 skip-gram,基于中心词 \(c\) 的某个上下文单词 \(c-m+j\) 对应的代价函数为: \[ - u_{c-m+j}^Tv_c + \log \sum_{k=1}^{|V|} \exp(u_k^Tv_c) \]
基于负采样的改进后的代价函数为: \[ - \log \sigma(u_{c-m+j}^T v_c) - \sum_{k=1}^{K} \log \sigma(-\tilde{u}_k^Tv_c) \] 对于 CBOW,给定上下文向量 \(\hat{v}\) 的中心词 \(u_c\) 对应的代价函数为: \[ -u_c^T\hat{v} + \log \sum_{j=1}^{|V|} \exp(u_j^T\hat{v}) \]
基于负采样的改进后的代价函数为: \[ - \log \sigma(u_{c}^T \hat{v}) - \sum_{k=1}^{K} \log \sigma(-\tilde{u}_k^T\hat{v}) \] 在上述公式中,\(\{\tilde{u}_k | k=1\ldots k\}\) 为负样本,随机采样自 \(P_n(w)\)。文献中指出目前最有效的 \(P_n(w)\) 是 Unigram Model 的 \(3/4\) 次幂。
Hierarchical Softmax
另一种优化代价函数计算的方法是 hierarchical softmax。在实际应用中,hierarchical softmax 对低频词的效果更好,而负采样对常用词和低维词向量的效果更好。
Hierarchical softmax 使用一个二叉树来表示词典中的所有词语。每个叶子节点都是一个词语,从根节点到叶子节点的路径唯一:
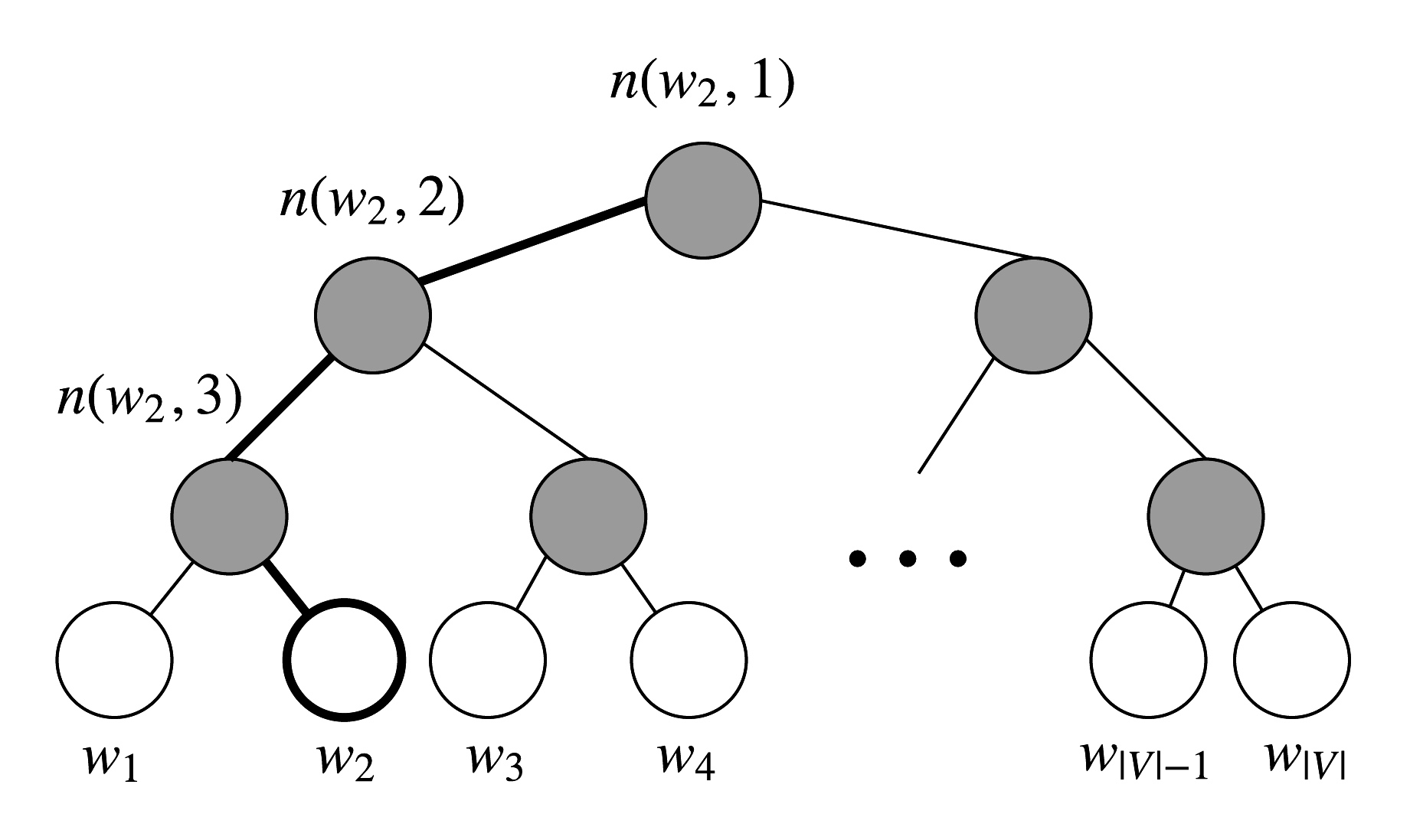
在 Hierarchical softmax 中,给定一个词向量 \(w_i\) ,一个词语 \(w\) 的概率 \(P(w|w_i)\) 等价于从根节点出发随机行走至 \(w\) 对应的叶子节点的概率。这样表示优点是其计算复杂度为 \(O((\log(|V|))\).
在该训练方法中,没有词语的输出表达(即 \(\mathcal{U}\) 矩阵)。取而代之的是每个节点(叶子节点除外)代表一个向量,模型需要去学习这些向量。
符号定义
为了更好地描述模型,给出如下定义: + \(L(w)\):从根节点到叶子节点 \(w\) 的节点数量(包括根节点但不包括叶子节点) + 例如上图中,\(L(w_2)\) 为 3 + \(n(w,i)\):在该路径上的第 \(i\) 个节点,对应的向量为 \(v_{n(w,i)}\) + \(n(w,1)\) 是根节点,\(n(w, L(w))\) 是 \(w\) 的父节点 + 对于每个内部节点 \(n\),我们以某种规则选择其的一个孩子节点(二选一),称为 \(ch(n)\) + 例如总是选择左边的孩子节点
训练方法
基于上述定义,\(P(w|w_i)\) 可以表示为: \[ P(w|w_i) = \prod_{j=1}^{L(w)-1} \sigma ([n(w,j+1) = ch(n(w,j))] \cdot v_{n(w,j)}^Tv_{w_i}) \]
其中: \[ [x] = \left\{ \begin{aligned} 1 \;\text{if x is true}\\ -1 \;\text{otherwise} \end{aligned} \right. \] 下面对上述公式进行解释:
首先,我们基于从根节点 \(n(w,1)\) 到叶子节点 \(n(w)\) 的路径计算向量的点积。 注意 \(v_{n(w,j)}\) 是节点词语对应的向量,\(v_{w_i}\) 则是基于输入矩阵得到的根节点词语的向量,两者并不相关,都需要学习。
然后,通过 sigmoid 函数得到每个节点的概率输出。\([n(w,j+1) = ch(n(w,j))]\) 保证了选择左边子节点和右边子节点的概率之和为 1: \[ \sigma(v_n^Tv_{w_i}) + \sigma(-v_n^Tv_{w_i}) = 1 \]
- 同时也保证了 \(\sum_{w=1}^{|V|} P(w|w_i) =1\)(将概率沿树向上累加可以证明)
最后,将节点概率相乘得到输出。以图中的 \(w_2\) 为例,其概率为:
\[ \begin{aligned} P(w_2|w_i) &= p(n(w_2,1),\text{left}) \cdot p(n(w_2,2),\text{left}) \cdot p(n(w_2,3),\text{right}) \\ &= \sigma (v^T_{n(w_2,1)}v_{w_i})\cdot\sigma (v^T_{n(w_2,2)}v_{w_i})\cdot\sigma (-v^T_{n(w_2,3)}v_{w_i}) \end{aligned} \] 为了训练模型,我们的目标依然是最小化负对数似然函数 \(-\log P(w|w_i)\),学习的参数为节点对应的向量以及输入矩阵。该方法的速度取决于二叉树的构建,原论文使用了一个二叉霍夫曼树(给予常用词更短的路径)。
Word2vec 的输出
不管使用哪种模型或训练方法,最终都会得到训练完成后的输入矩阵 \(\mathcal{V}\)。我们所需要的词向量通过 one-hot 向量与输入矩阵相乘得到(即为模型的隐藏层): \[ v_{output} = \mathcal{V}x_{input} \]
思维导图
