CS224N 学习笔记之二:词向量 2
本篇博客为 CS224N 学习笔记第二部分,主题是:词向量(GloVe,评估和训练)。
GloVe
与之前方法的比较
之前我们介绍了两种表示词向量的方法:基于数量的矩阵分解方法(HAL & LSA)和基于窗口的概率方法(word2vec)。第二种方法明显优于第一种,但其只考虑了一个较小窗口内的词语信息,没有利用好全局的词语共现数据。
Glove 结合了上述两种方法的优点:其使用全局数据来基于上下文 \(i\) 预测一个词语 \(j\) 的概率,目标函数为最小二乘函数。
共现矩阵
首先我们需要计算词语的共现矩阵,现给出如下定义: + \(X\):表示词语之间的共现矩阵 + \(X_{ij}\):表示词语 \(j\) 与上下文词语 \(i\) 的共现次数 + \(X_i= \sum_k X_{ik}\):表示任意词语 \(k\) 与上下文词语 \(i\) 的共现次数 + \(P_{ij} = P(w_j | w_i) = \frac {X_{ij}} {X_i}\):表示词语 \(j\) 以词语 \(i\) 为上下文的概率
虽然当语料库很大时,该矩阵的计算十分复杂,但这是一次性的工作,所以可以接受。
最小二乘目标函数
在 word2vec 中,我们使用 softmax 来计算给定上下文词语 \(i\) 的词语 \(j\) 的概率: \[ Q_{ij} = \frac {\exp (u_j^Tv_i)} {\sum_{w=1}^W \exp(u_w^Tv_i)} \]
之前的训练都是使用随机梯度下降,如果计算全局的代价函数,则为: \[ J = - \sum_{i \in corpus} \sum_{j \in context(i)} \log Q_{ij} \]
这里使用了对数最大似然(可以理解为 softmax 向量与 one-hot 向量的交叉熵)。
上式中相同的 \(i\) 和 \(j\) 的组合可能出现多次(多次共现) ,我们可以利用共现矩阵将相同的 \(i\) 和 \(j\) 先累加起来,以减少运算: \[ J = -\sum_{i=1}^W\sum_{j=1}^W X_{ij} \log{Q_{ij}} \]
根据之前的定义,我们可以将上式改写为: \[ J = -\sum_{i=1}^W X_i \sum_{j=1}^W P_{ij} \log{Q_{ij}} =-\sum_{i=1}^W X_iH(P_i,Q_i) \]
其中 \(H(P_i, Q_i)\) 是分布 \(P_i\) 和 \(Q_i\) 的交叉熵。注意该交叉熵与上一步得到的交叉熵并不相同,在分类问题中,交叉熵函数与最大似然函数等价。
交叉熵代价函数的不足之处在于其分布需要归一化,即在整个语料库上进行求和。为了避免这一复杂的运算,我们使用非归一化的分布的最小二乘函数来取代交叉熵函数: \[ \hat{J} = -\sum_{i=1}^W \sum_{j=1}^W X_{i}(\hat{P}_{ij} - \hat{Q}_{ij})^2 \]
其中 \(\hat{P}_{ij} = X_{ij}\),\(\hat{Q}_{ij} = \exp(u_j^Tv_i)\)。
上述代价函数的一个新问题是 \(X_{ij}\) 经常过大,导致优化困难。我们通过取对数来解决这一问题:
\[ \begin{aligned} \hat{J} &= -\sum_{i=1}^W \sum_{j=1}^W X_{i}(\log(\hat{P}_{ij}) - \log(\hat{Q}_{ij})^2 \\ &= -\sum_{i=1}^W \sum_{j=1}^W X_{i}(u_j^Tv_i - \log X_{ij})^2 \end{aligned} \] 在上述代价函数中,根据观察,权重因子 \(X_i\) 并不是一个最佳的选择。我们将使用一个更一般化的权重函数,其依赖于上下文单词:
\[ \hat{J} = -\sum_{i=1}^W \sum_{j=1}^W f(X_{ij})(u_j^Tv_i - \log X_{ij})^2 \]
结论
GloVe 模型高效地使用了全局信息。其只训练词语共现矩阵中不为零的元素,输出一个较有意义的子空间向量。在词语类比任务上,GloVe 比 word2vec 表现更好,且速度更快。
词向量的评估
本节将定量评估生成的词向量的质量。
内在评估
内在评估是指用某种具体的中间任务(比如类比补全)来评估词向量。这些子任务一般比较简单,计算复杂度较低,可以帮助我们快速理解该系统的好坏。该评估方法应该与词向量的最终应用正相关(能反映出词向量应用到下游系统时的表现)。
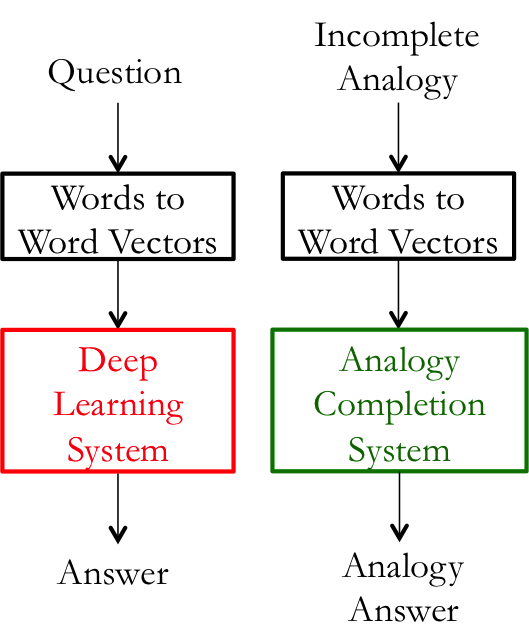
外在评估
外在评估即基于实际任务的评估。这种评估通常计算复杂度较高,训练时间长。一般来说,对整个系统的评估难以确定是哪个子系统发生了问题,这时还需要借助内在评估来确定问题:基于内在评估替换不同的子系统,如果整体表现提升,则保持替换。
内在评估案例:词向量类比
一个经典的内在评估方法就是词向量类比补全。在一个词向量类比中,我们会给出如下形式的不完全类比: \[ a:b::c:? \] 内在评估系统希望找出能够最大化如下余弦相似度的词向量: \[ d = \arg \max_i \frac {(x_b-x_a+x_c)^Tx_i}{||x_b-x_a+x_c||} \]
直观上来看,理想情况下我们希望 \(x_b - x_a = x_d - x_c\),即 \(x_b - x_a + x_c = x_d\)。因此我们要找到能够最大化等式左右两个向量夹角的词向量 \(x_d\)。注意这里默认 \(x_d\) 已经进行归一化处理,所以不用除以其模。
词向量的类比可以是语义层面的,也可以是语法层面的。有时候由于语料库的影响,语义类比可能产生导致不同的结果,在下面的例子中,一个国家的首都在不同时期可能不同:
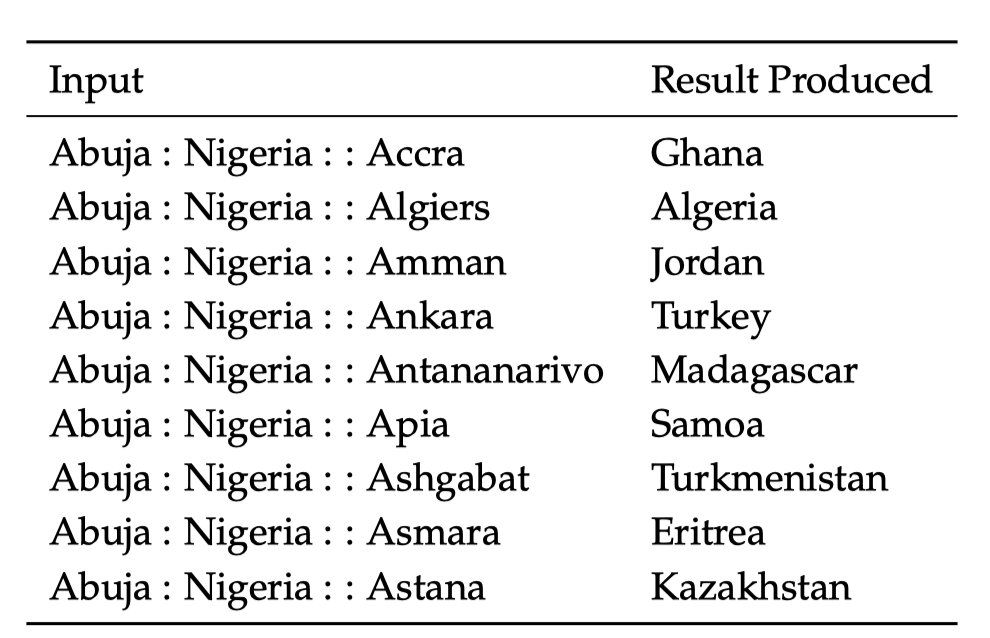
一个语法层面类比的例子如下所示,我们类比了形容词和其最高级:
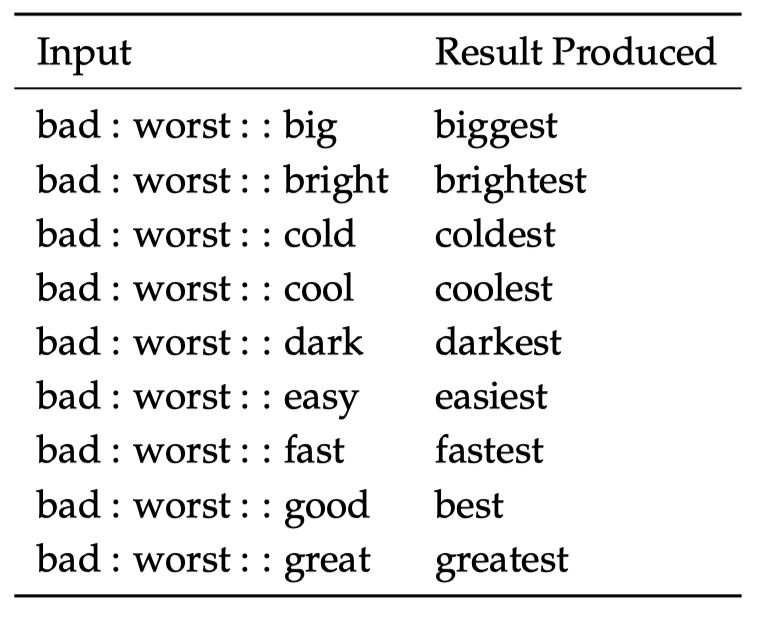
内在评估调整案例:类比评估
我们可以基于内在评估系统来调整词向量模型的超参数,包括:
- 词向量维数
- 语料库大小
- 语料库来源/类型
- 上下文窗口大小
- 上下文对称性
下表给出了不同模型使用不同超参数在类比问题上的表现对比:
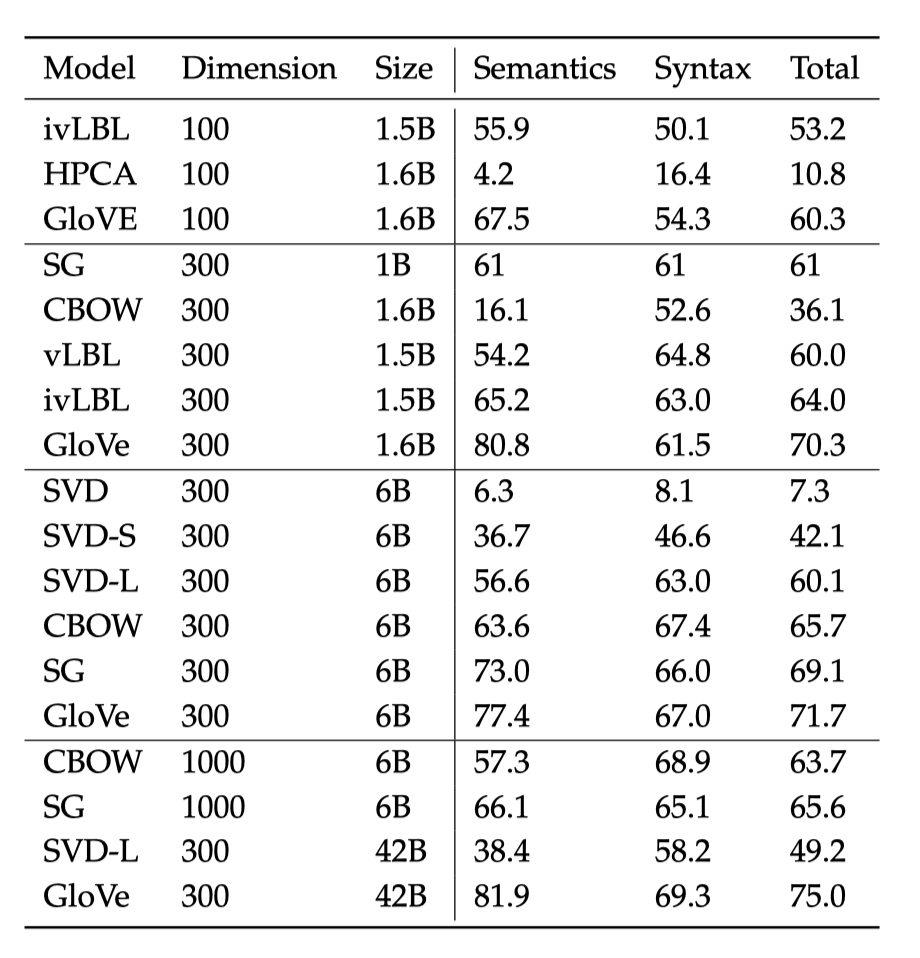
基于该表可以得出以下三点结论:
- 表现非常依赖于模型。即不同的方法得出的词向量表现差距较大
- 随着语料库的增加,表现逐渐提升。这表示可以学习的经验变多了
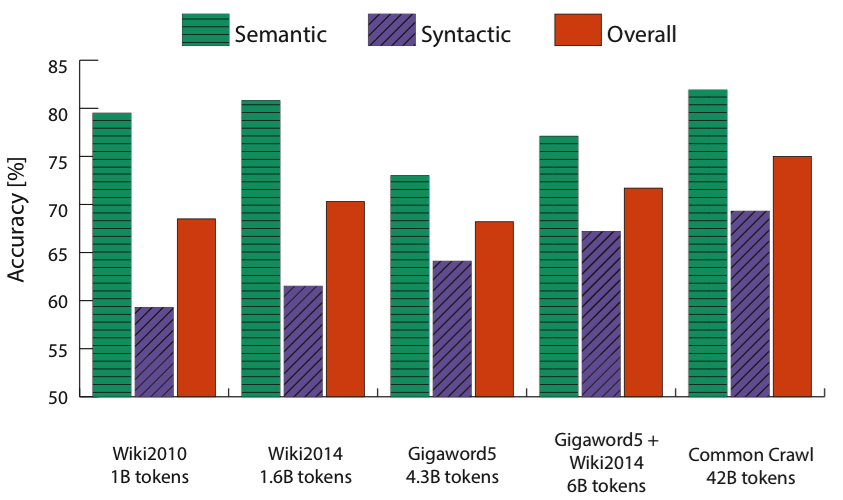
- 对于非常低维的词向量,表现较差。低维词向量难以捕捉到词语之间的不同含义,这可以理解为模型复杂度不同导致的高偏差问题。直观上来看,非常高维的词向量会导致高方差问题(过拟合),即捕捉到了语料库的噪声,结果不具有可推广性。但研究表明 skip-gram、Glove 方法得出的词向量对过拟合具有鲁棒性
下图给出了不同超参数对 Glove 表现的影响:
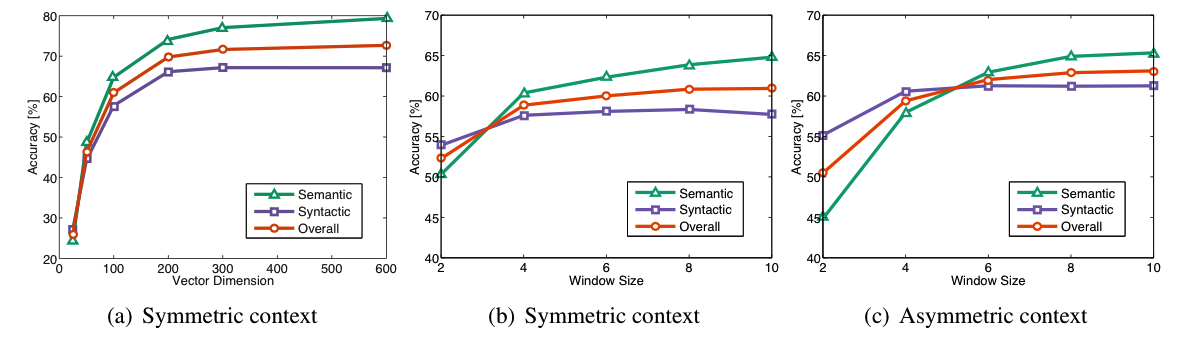
除了上述因素,训练时间也对表现的提升有一定影响:
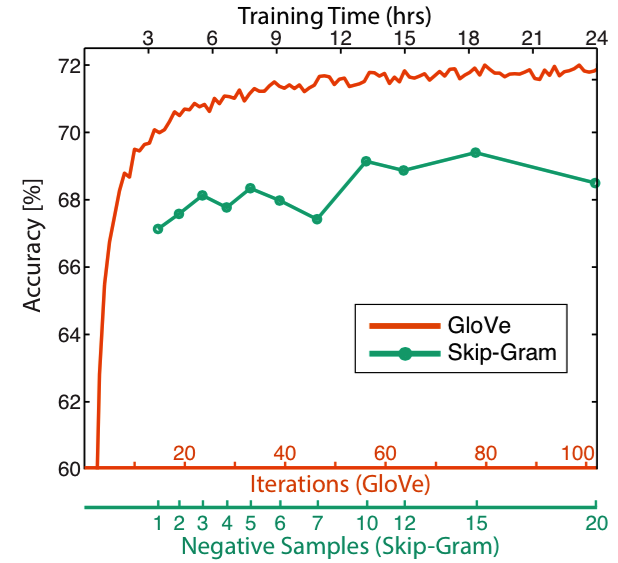
内在评估案例:相关性评估
另一种评估词向量质量的简单方法是将人工标注的词语相似度(如 0-10)与词向量之间的余弦相似度进行比较。这种方法需要基于人工标注的数据集。下表展示了不同的词向量生成方法在不同的人工判断数据集上的表现:
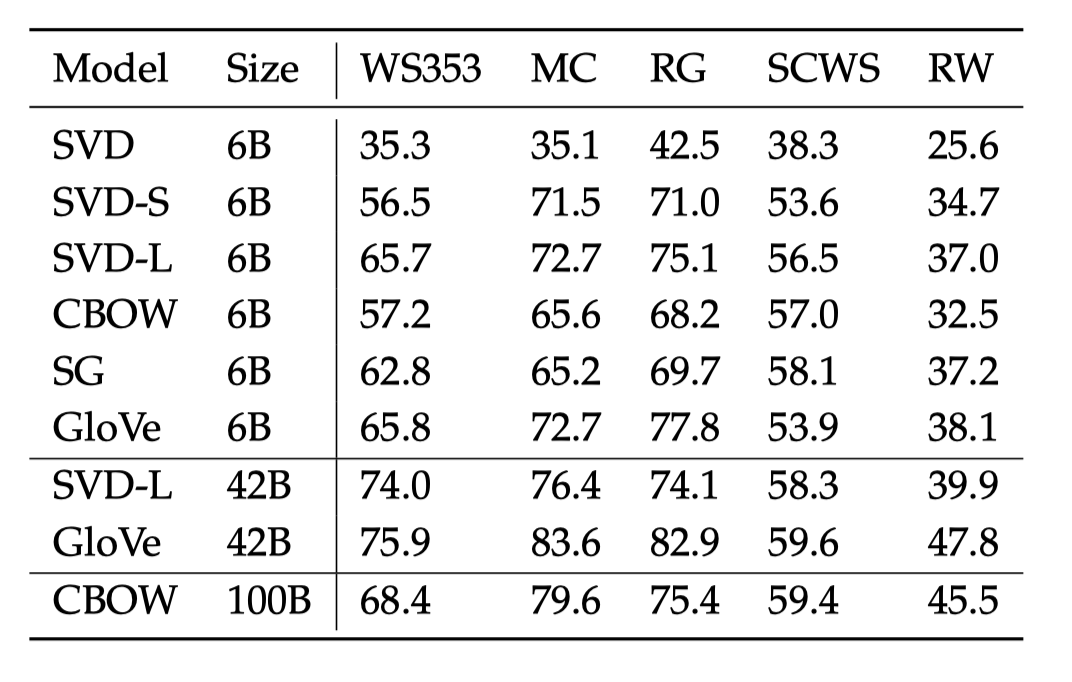
扩展阅读:处理歧义
对于某些词语,其在不同的上下文中意义不同。对于这种情况,这里给出了一种处理方法:
- 对于所有出现的词语,以固定的窗口大小收集其上下文(如前 5 个单词加后 5 个单词)
- 对于每个上下文,使用上下文词向量的加权平均表示(idf 加权)
- 使用球面 K-means 对这些上下文表示聚类
- 最后,每个词语都会重新标记为与其关联的类,基于这个类训练其词向量。这样对于同时属于不同类的词语,就会得到多个词向量
PS:随着上下文词嵌入的出现,我们已经可以更优雅地得到动态词向量了。
外在任务训练
大部分现实世界问题的最终目标是将词向量用于某些外在任务,下面我们介绍处理外在任务的一般方法。
问题的提出
大部分 NLP 的外在任务都可以看作分类问题,比如情感分类,命名实体识别等。对于这些问题,我们一般有如下的训练集形式:
\[ \{x^{(i)},y^{(i)}\}_1^N \]
其中 \(x^{(i)}\) 是一个 d-维的词向量,通过某种词嵌入技术生成。\(y^{(i)}\) 是一个 C 维的 one-hot 向量,表示我们希望预测的标签(类别)。
在经典的机器学习任务中,我们通常保持输入数据与输出标签不变,使用优化方法来训练参数(权重)。但是在 NLP 任务中,我们在训练外在任务时可能会重新训练输入词向量。
重新训练词向量
在执行一个外在任务时,词向量通常先基于一个简单的内在任务进行优化。很多情况下,初始词向量都是一个不错的选择,可以取得较好的表现。如果训练集足够大,那么有时候进一步训练词向量可能会得到更好的结果。
然而,这一操作是有风险的。如果训练集不够大,重新训练词向量可能会使得表现变差。因为 Word2Vec 或 GloVe 得到的语义相关的词向量在向量空间中距离较近,如果在一个小词库中重新训练,可能会导致词向量出现偏移。
下面介绍一个二维词向量分类的例子。首先是没有重新训练情况下分类正确的情况:
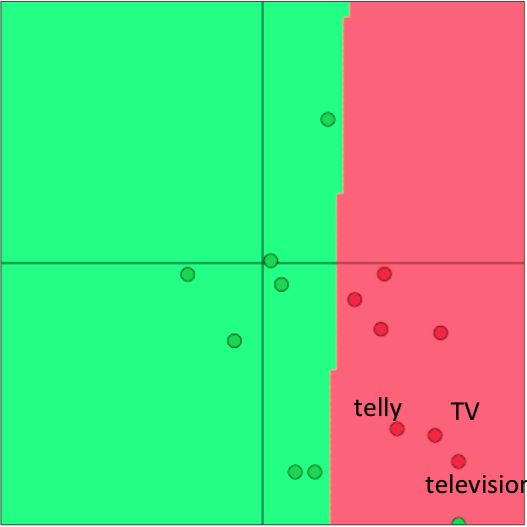
在这些词语中,telly 和 TV 位于外在任务的训练集中,而 televison 只位于测试集中(图示为测试集结果)。然后是重新训练后分类不正确的情况:
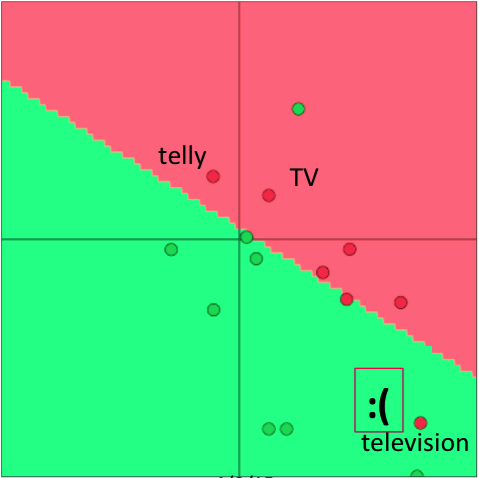
重新训练后 telly 和 TV 发生了偏移,而 television 没有变化,但决策边界发生了变化,因此导致分类出现了错误。
Softmax 分类和正则化
考虑使用如下形式的 softmax 分类函数: \[ p(y_j=1|x) = \frac {\exp(W_jx)}{\sum_{c=1}^C\exp(W_cx)} \]
这里计算的是词向量 \(x\) 属于类别 \(j\) 的概率。使用交叉熵损失函数,可以得到一个训练样本的损失如下: \[ -\sum_{j=1}^C y_j \log(p(y_j=1|x)) = -\sum_{j=1}^C y_j \log \left(\frac {\exp(W_jx)}{\sum_{c=1}^C\exp(W_cx)} \right) \]
因为 \(y_j\) 只有一个 index 为 1(一般情况下),所以定义 \(k\) 为正确类别的 index,则上述损失可以简写为: \[ - \log \left(\frac {\exp(W_kx)}{\sum_{c=1}^C\exp(W_cx)}\right) \] 对于由 N 个点构成的数据集,代价函数为: \[ -\sum_{i=1}^N \log \left(\frac {\exp(W_{k(i)}x)}{\sum_{c=1}^C\exp(W_cx)}\right) \]
其中 \(k(i)\) 为一个函数,返回样本 \(x^{(i)}\) 的正确分类 index。
对于上述代价函数,如果要训练模型权重 \(W\) 和词向量 \(x\),需要更新的参数量是多少呢?对于一个简单的线性分类器,假设其输入为一个 \(d\) 维词向量,输出为一个含有 \(C\) 个类别的分布。关于模型权重需要更新 \(C \cdot d\) 个参数,关于所有词向量需要更新 \(|V| \cdot d\) 个参数。因此,总的更新参数为 \(C \cdot d + |V| \cdot d\) 个:
\[ \nabla_\theta J(\theta) = \left[\begin{array}{cc} \nabla _{W_{\cdot 1}} \\ \vdots \\ \nabla _{W_{\cdot d}} \\ \nabla _{x_{aardvark}} \\ \vdots \\ \nabla _{x_{zebra}} \end{array} \right] \]
如此大的参数量很容易引起过拟合。为了减小过拟合的风险,我们引入一个正则项。其利用了贝叶斯学派的理论,对参数的规模进行了限制: \[ -\sum_{i=1}^N \log \left(\frac {\exp(W_{k(i)}x)}{\sum_{c=1}^C\exp(W_cx)}\right) + \lambda \sum_{k=1}^{C\cdot d + |V| \cdot d} \theta_k^2 \]
最小化上述的代价函数可以减小参数规模过大引起过拟合的可能性。如果相关权重 \(\lambda\) 调整适当,能够提升模型的可推广性。
窗口分类
之前我们使用的输入是单个词向量,实际上,在不同的上下文中相同词语有着不同的含义(语义或语法层面)。因此,我们一般使用一个词语序列作为输入,该序列包含一个中心词及其上下文,上下文的单词数量由上下文窗口大小决定。
对于不同的问题,上下文窗口的大小会发生变化,一般来说:
- 较小的窗口在语法层面上的表现更好
- 较大的窗口在语义层面上的表现更好
为了修改之前提到的 softmax 函数,用于基于窗口的词语分类,我们将 \(x^{(i)}\) 用 \(x^{(i)}_{window}\) 代替: \[ x^{(i)}_{window} = \left[\begin{array}{cc} x^{(i-2)} \\ x^{(i-1)} \\ x^{(i)} \\ x^{(i+1)} \\ x^{(i+2)} \end{array} \right] \]
计算关于词语的损失梯度如下所示: \[ \delta_{window} = \left[\begin{array}{cc} \nabla _{x^{(i-2)}} \\ \nabla _{x^{(i-1)}} \\ \nabla _{x^{(i)}} \\ \nabla _{x^{(i+1)}} \\ \nabla _{x^{(i+2)}} \end{array} \right] \]
实现时需要分配梯度来更新相应的词向量。
非线性分类器
线性分类器能力有限,难以处理非线性的边界:
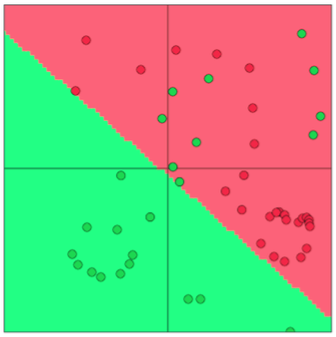
下节开始我们将介绍神经网络,用以处理非线性的决策边界:
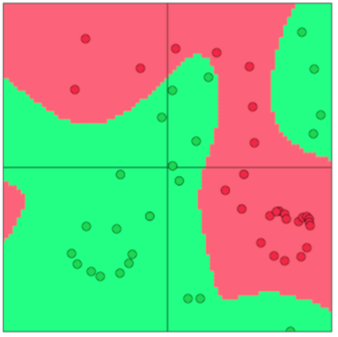
思维导图
