CS229 学习笔记之十五:强化学习与控制
本篇博客为 CS229 学习笔记第十五部分,主题是:强化学习。
本章将开始介绍强化学习与适应性控制。在监督学习中,对于训练集我们均有明确的标签,算法只需要模仿训练集中的标签来给出预测即可。但对于某些情况,例如序列性的决策过程和控制问题,我们无法构建含有标签的训练集。即无法提供一个明确的监督学习算法来进行模仿。
在强化学习的框架下,我们只会给出一个奖励函数(reward function),该函数会告知学习程序(leaning agent)什么时候的动作是好的,什么时候的是不好的。算法的工作是找出随着时间推移如何选择动作来得到最大的奖励。
强化学习已经成功用于多种场景,包括:无人直升机的自主飞行、机器人行走、手机网络路由、市场策略选择、工厂控制、高效率的网页索引等。我们将从马尔可夫决策过程开始介绍强化学习,其给出了强化学习问题的常见形式。
马尔可夫决策过程
一个马尔可夫决策过程是一个五元组 \(\left(S, A,\left\{P_{s a}\right\}, \gamma, R\right)\),其中:
- \(S\) 是一个状态集。例如在无人直升机的自主飞行中,\(S\) 可以是直升机所有可能的位置与方向;
- \(A\) 是一个动作集。例如你可以推动直升机控制摇杆的所有方向;
- \(P_{sa}\) 是状态转移概率,对于每个状态 \(s \in S\) 以及动作 \(a \in A\),\(P_{sa}\) 为状态空间上的分布。简单来说,\(P_{sa}\) 给出当我们在状态 \(s\) 采取了行动 \(a\) 时,下一个状态的分布;
- \(\gamma \in[0,1)\) 被称为折扣因子(discount factor);
- \(R : S \times A \mapsto \mathbb{R}\) 为奖励函数。有时候奖励函数被写作仅与状态 \(S\) 相关,即 \(R : S \mapsto \mathbb{R}\)。
马尔可夫决策过程(MDP)的执行如下:我们从某个状态 \(s_0\) 开始,选择某个动作 \(a_{0} \in A\) 来执行 MDP;作为选择的结果,MDP 的状态将随机转移到某个后继状态 \(s_{1} \sim P_{s_{0} a_{0}}\);然后,我们需要选择另一个动作 \(a_1\),作为结果,状态会转移至 \(s_{2} \sim P_{s_{1} a_{1}}\);接下来再选择一个动作 \(a_2\),以此类推。
该过程可以用下图表示: \[ s_{0} \stackrel{a_{0}}{\longrightarrow} s_{1} \stackrel{a_{1}}{\longrightarrow} s_{2} \stackrel{a_{2}}{\longrightarrow} s_{3} \stackrel{a_{3}}{\longrightarrow} \ldots \]
遍历序列中的所有状态和动作,总的收益为: \[ R\left(s_{0}, a_{0}\right)+\gamma R\left(s_{1}, a_{1}\right)+\gamma^{2} R\left(s_{2}, a_{2}\right)+\cdots \]
当将奖励函数仅与状态相关时,收益变为: \[ R\left(s_{0}\right)+\gamma R\left(s_{1}\right)+\gamma^{2} R\left(s_{2}\right)+\cdots \] 本章将主要使用简单的状态奖励函数 \(R(s)\),推广至 \(R(s, a)\) 并不困难。
在强化学习中,我们的目标就是找到一组动作,来最大化总收益的期望: \[ \mathrm{E}\left[R\left(s_{0}\right)+\gamma R\left(s_{1}\right)+\gamma^{2} R\left(s_{2}\right)+\cdots\right] \]
注意在时间步 \(t\) 的奖励通过参数 \(\gamma^t\) 进行了缩减。因此,为了使得期望较大,我们希望尽可能早地积累正奖励,尽可能推迟负奖励。
策略(policy)指的是将状态映射为动作的任意函数 \(\pi : S \mapsto A\)。任意时刻,当我们处在状态 \(s\),我们采取了行动 \(a=\pi(s)\),则我们执行了策略 \(\pi\)。我们定义一个策略 \(\pi\) 的值函数为: \[ V^{\pi}(s)=\mathrm{E}\left[R\left(s_{0}\right)+\gamma R\left(s_{1}\right)+\gamma^{2} R\left(s_{2}\right)+\cdots | s_{0}=s, \pi\right] \]
\(V^{\pi}(s)\) 即为从状态 \(s\) 开始,根据策略 \(\pi\) 选择动作所积累的折扣奖励函数的期望。注意 \(\pi\) 并非随机变量,上述表示只是一种习惯。
给定一个策略 \(\pi\),其值函数满足贝尔曼等式: \[ V^{\pi}(s)=R(s)+\gamma \sum_{s^{\prime} \in S} P_{s \pi(s)}\left(s^{\prime}\right) V^{\pi}\left(s^{\prime}\right) \]
这表示期望和由两部分组成:
- 即时奖励 \(R(s)\)
- 未来的折扣奖励的期望和(第一步之后),也可以写作 \(\mathrm{E}_{s^{\prime} \sim P_{s \pi(s)}}\left[V^{\pi}\left(s^{\prime}\right)\right]\)
贝尔曼等式可以用于求解 \(V^{\pi}\)。在一个有限状态的 MDP 中,我们可以对于每个状态 \(s\) 写出其 \(V^{\pi}(s)\) 的等式,这可以给出一个含有 \(|S|\) 个变量的 \(|S|\) 个线性方程,用于进行求解,变量即每个状态的未知 \(V^{\pi}(s)\)。
我们定义最优值函数为: \[ V^{*}(s)=\max _{\pi} V^{\pi}(s) \tag{1} \]
其表示在所有策略中,可以得到的最大期望和。该函数同样满足贝尔曼等式: \[ V^{*}(s)=R(s)+\max _{a \in A} \gamma \sum_{s^{\prime} \in S} P_{s a}\left(s^{\prime}\right) V^{*}\left(s^{\prime}\right) \tag{2} \]
第一部分与之前一样,为即时奖励;第二部分为所有动作中最大的未来期望和。
我们可以定义策略 \(\pi^{*} : S \mapsto A\) 为: \[ \pi^{*}(s)=\arg \max _{a \in A} \sum_{s^{\prime} \in S} P_{s a}\left(s^{\prime}\right) V^{*}\left(s^{\prime}\right) \tag{3} \]
\(\pi^{*}(s)\) 给出了动作 \(a\) 来使得 \((2)\) 式最大化。
根据上述定义,我们可以推导出如下事实:对于每一个状态 \(s\) 和每一种策略 \(\pi\),都有: \[ V^{*}(s)=V^{\pi^{*}}(s) \geq V^{\pi}(s) \]
这个公式表明 \((3)\) 式中定义的策略即为最优策略。注意 \(\pi^{*}\) 有一个有趣的特性:其为所有状态 \(s\) 的最优策略,因为其定义为状态集到动作集的映射。这意味着无论 MDP 的初始状态是什么,我们都可以使用同样的最优策略 \(\pi^{*}\)。
值迭代和策略迭代
下面介绍求解有限状态 MDP 的两种高效算法:值迭代和策略迭代。我们目前只考虑有限状态和动作空间的 MDP。
值迭代
值迭代算法的流程为:
- 对于每个状态 \(s\),初始化 \(V(s) :=0\)
- 重复下述过程直至收敛:对于每个状态 \(s\),更新 \(V(s) :=R(s)+\max _{a \in A} \gamma \sum_{s^{\prime}} P_{s a}\left(s^{\prime}\right) V\left(s^{\prime}\right)\)
该算法可以理解为不断更新 \((2)\) 式中的值函数。算法的内循环有两种更新方法:
- 同步更新:计算所有状态的 \(V(s)\),然后全部替换旧的值
- 异步更新:按某种顺序遍历状态,一次更新一个值
不论是异步还是同步更新,值迭代算法最终都会使 \(V\) 收敛至 \(V^*\)。得到了 \(V^*\),我们就可以利用 \((3)\) 式来找出最优策略。
策略迭代
策略迭代的流程为:
- 随机初始化 \(\pi\)
- 重复下述过程直至收敛:
- 令 \(V :=V^{\pi}\)
- 对于每个状态 \(s\),更新 \(\pi(s) :=\arg \max _{a \in A} \sum_{s^{\prime}} P_{s a}\left(s^{\prime}\right) V\left(s^{\prime}\right)\)
可以看到,该算法在内循环中计算当前策略的值函数,然后使用当前值函数更新策略。该步骤中找出的策略也被称为关于 \(V\) 的贪婪策略。在有限次数的迭代后,\(V\) 将收敛至 \(V^*\),\(\pi\) 将收敛至 \(\pi^*\)。注意:在内循环第一步中值函数的求解方式如之前所述,为含有 \(|S|\) 个变量的线性方程组。
值迭代和策略迭代是求解 MDP 的标准算法,目前没有好坏之分。一般对于较小的 MDP,策略迭代往往更快,迭代次数较少;而对于较大状态空间的 MDP,求解 \(V^{\pi}\) 相对较难,通常使用值迭代。在实际应用中,值迭代比策略迭代要使用得更加频繁(因为实际问题中状态通常较多)。
马尔可夫过程的模型学习
在实际问题中,我们无法得知状态转移概率和奖励函数,因此需要基于数据来进行估计。例如我们进行了一系列实验,得到如下所示的一系列马尔可夫过程:
\[ \begin{array}{l}{s_{0}^{(1)} \stackrel{a_{0}^{(1)}}{\longrightarrow} s_{1}^{(1)} \stackrel{a_{1}^{(1)}}{\longrightarrow} s_{2}^{(1)} \stackrel{a_{2}^{(1)}}{\longrightarrow} s_{3}^{(1)} \stackrel{a_{3}^{(1)}}{\longrightarrow} \ldots} \\ {s_{0}^{(2)} \stackrel{a_{0}^{(2)}}{\longrightarrow} s_{1}^{(2)} \stackrel{a_{1}^{(2)}}{\longrightarrow} s_{2}^{(2)} \stackrel{a_{2}^{(2)}}{\longrightarrow} s_{3}^{(2)} \stackrel{a_{3}^{(2)}}{\longrightarrow} \ldots} \\ {\ldots}\end{array} \]
其中 \(s_{i}^{(j)}\) 表示实验 \(j\) 的时间点 \(i\) 的状态,其对应的动作为 \(a_{i}^{(j)}\)。在实际中,每个实验可以运行至马尔可夫过程终止,或某个较大但有限的时间点。
基于上述"经验",我们可以利用极大似然估计来求出状态转移概率: \[ P_{s a}\left(s^{\prime}\right)=\frac{\# \text { times took we action } a \text { in state } s \text { and got to } s^{\prime}}{\# \text { times we took action a in state } s} \tag{4} \]
如果比例为 \(0/0\),则使用 \(1/|S|\) 替代。当我们进行更多的实验,得到更多的"经验"时,我们可以用一种较高效的方法来更新状态转移概率:具体来说,我们可以记录上式的分子与分母值,新的数据直接在旧数据的基础上累加即可。类似地,如果奖励函数 \(R\) 未知,我们可以用状态 \(s\) 的期望即时奖励估计 \(R(s)\) 来作为其平均奖励。
在学习出 MDP 的模型后,我们可以使用值迭代或策略迭代来求解 MDP,找出最佳策略。例如,将模型学习和值迭代结合在一起,我们可以得出下面的算法,用于未知概率转移矩阵的 MDP 的学习:
- 随机初始化 \(\pi\)
- 重复下述过程:
- 在 MDP 中执行 \(\pi\) 若干次来得到样本(下一步的状态通过观察得到)
- 使用 MDP 中的累加经验来估计 \(P_{sa}\) (以及 \(R\),如果需要)
- 基于估计的状态转移概率和奖励函数应用值迭代算法,得到一个新的 \(V\) 的估计
- 更新 \(\pi\) 为关于 \(V\) 的贪婪策略
对于该算法,可以通过下述手段来使其运行更快:在第二步的值迭代的内循环中,每次不初始化 \(V\) 为 0,而初始化为上一次外循环中得到的结果。
连续状态马尔可夫决策过程
到目前为止,我们都在讨论有限数量状态下的 MDP,现在我们将开始讨论无限状态下的 MDP (\(S=\mathbb{R}^{n}\))。
离散化
求解连续状态 MDP 的最简单的方法就是离散化状态空间,然后使用之前提到的值迭代或状态迭代算法。例如,对于一个二维状态 \((s_1,s_2)\),我们可以用一个网格来进行离散化:
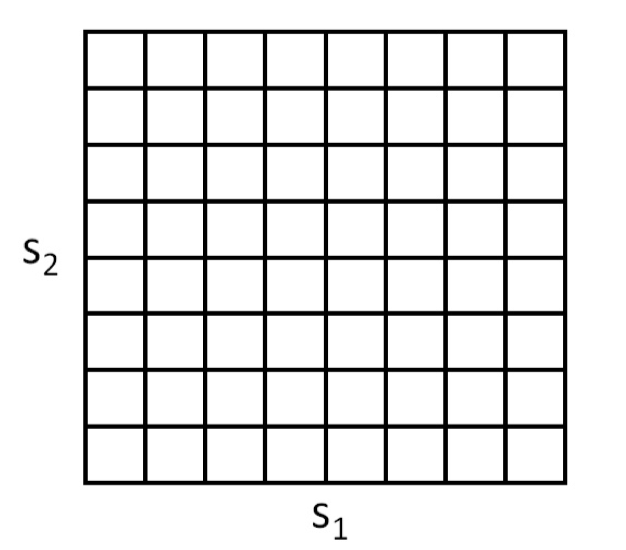
每一个网格细胞代表一个独立的离散状态 \(\bar{s}\),然后我们就可以用一个离散状态的 MDP \(\left(\bar{S}, A,\left\{P_{\overline{s} a}\right\}, \gamma, R\right)\) 来估计连续状态下的 MDP,使用值迭代或策略迭代来求解 \(V^{\star}(\bar{s})\) 和 \(\pi^{\star}(\bar{s})\)。当实际的系统处于某个连续值的状态 \(s \in S\) 时,我们先计算其对应的离散状态 \(\bar{s}\),然后执行最优策略 \(\pi^{\star}(\bar{s})\)。
离散化的方法对很多问题都有较好的效果,但其存在两点不足:
第一点是对 \(V^{\star}\) 和 \(\pi^{\star}\) 的表达过于 naive,即假设其在离散的区段上取值不变。例如下面的线性回归问题,如果使用离散化来表达,则得到如下结果:
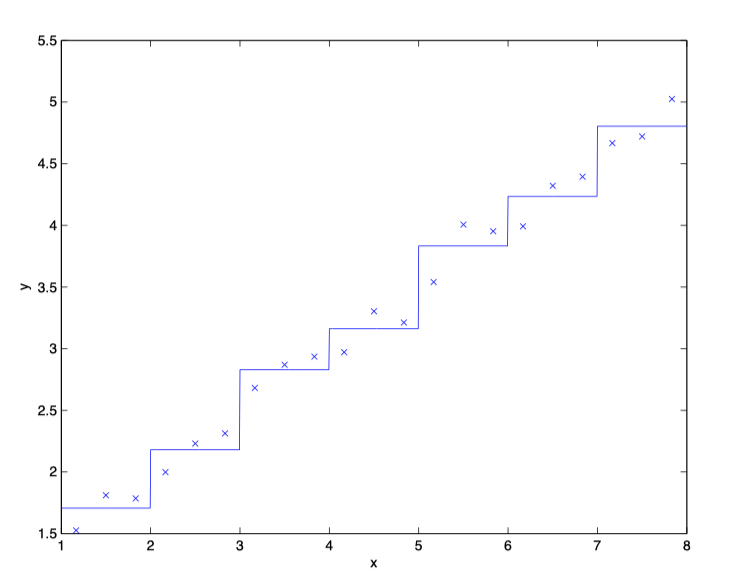
可以看出离散化对光滑数据的拟合并不好,我们可能需要更加精确的离散化(非常小的网格)来获得精确的估计。
第二点是维度诅咒(curse of dimensionality)。假设 \(S=\mathbb{R}^{n}\),且我们将每个维度的状态离散化为 \(k\) 个值,则总的离散状态数为 \(k^n\)。其随着维数的增加呈指数上升趋势,难以推广至大型问题。从经验上来说,离散化对 1 维和 2 维问题的效果最好,如果注意离散化的方法,则其对 4 维以下问题也效果不错,如果你特别牛批,甚至能应用到 6 维问题,再高的话基本上就不行了。
值函数近似
下面介绍另一种直接在连续状态 MDP 中寻找最佳策略的方法。我们将直接估计 \(V^{\star}\) ,而不去进行离散化。该方法称为值函数近似,已经成功应用于许多强化学习问题。
使用一个模型或模拟器
为了设计一个值函数估计算法,需要先假设我们有一个模型(或模拟器)。对于 MDP,通俗来说,模拟器就是一个黑盒子,接收输入状态 \(s_t\) (连续值)和动作 \(a_t\),根据状态转移概率 \(P_{s_ta_t}\) 输出下一个状态 \(s_{t+1}\) ,:
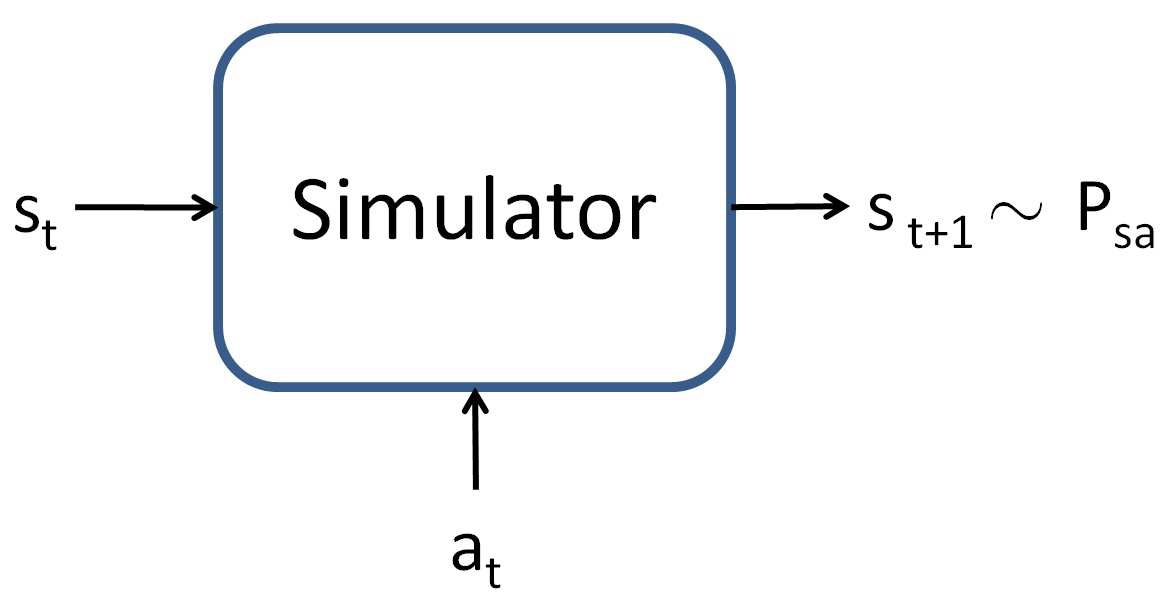
我们有多种方式来得到上述模型。第一种方法是使用物理模拟。例如使用软件包来对某些问题进行物理描述,进行模拟;第二种方法是从已有的数据中进行学习。例如,假设我们在一个 MDP 中执行 \(m\) 次试验,每次试验包含 T 个时间步,动作的选择可以随机或是执行某种特定的策略,或是其他方式。然后,我们会得到如下的 \(m\) 个观察序列:
\[ \begin{array}{c}{s_{0}^{(1)} \stackrel{a_{0}^{(1)}}{\longrightarrow} s_{1}^{(1)} \stackrel{a_{1}^{(1)}}{\longrightarrow} s_{2}^{(1)} \stackrel{a_{2}^{(1)}}{\longrightarrow} \cdots \stackrel{a_{T-1}^{(1)}}{\longrightarrow} s_{T}^{(1)}} \\ {s_{0}^{(2)} \stackrel{a_{0}^{(2)}}{\longrightarrow} s_{1}^{(2)} \stackrel{a_{1}^{(2)}}{\longrightarrow} s_{2}^{(2)} \stackrel{a_{2}^{(2)}}{\longrightarrow} \cdots \stackrel{a_{T-1}^{(2)}}{\longrightarrow} s_{T}^{(2)}} \\ {\cdots} \\ {s_{0}^{(m)} \stackrel{a_{0}^{(m)}}{\longrightarrow} s_{1}^{(m)} \stackrel{a_{1}^{(m)}}{\longrightarrow} s_{2}^{(m)} \stackrel{a_{2}^{(m)}}{\longrightarrow} \cdots \stackrel{a_{T-1}^{(m)}}{\longrightarrow} s_{T}^{(m)}}\end{array} \]
我们会使用一个学习算法来将 \(s_{t+1}\) 表示为 \(s_t\) 和 \(a_t\) 的函数。一种可能的线性模型如下: \[ s_{t+1}=A s_{t}+B a_{t} \tag{5} \]
我们可以使用试验中收集到的数据来估计参数: \[ \arg \min _{A, B} \sum_{i=1}^{m} \sum_{t=0}^{T-1}\left\|s_{t+1}^{(i)}-\left(A s_{t}^{(i)}+B a_{t}^{(i)}\right)\right\|^{2} \] 学习到了 \(A\) 和 \(B\) 后,一种选择是建立一个决定性模型,即给定输入 \(s_t\) 和 \(a_t\) 后,输出 \(s_{t+1}\),例如式 \((5)\);另一种选择是建立一个随机模型,即 \(s_{t+1}\) 是输入的随机函数:
\[ s_{t+1}=A s_{t}+B a_{t}+\epsilon_{t} \]
其中 \(\epsilon_{t}\) 是噪声项,分布为 \(\epsilon_{t} \sim \mathcal{N}(0, \Sigma)\),\(\Sigma\) 也可以从数据中学习。
需要注意,上面我们所列举的都是线性模型,实际上非线性模型(例如定义 \(s_{t+1}=A \phi_{s}\left(s_{t}\right)+B \phi_{a}\left(a_{t}\right)\))或非线性学习算法(例如局部加权线性回归)都可以用于构建模拟器。
拟合值迭代
下面介绍用于估计连续状态 MDP 值函数的拟合值迭代算法。这里假设状态空间连续,但动作空间较小且离散(一般来说,动作集的离散化相对容易很多)。
在值迭代中,我们会进行如下更新: \[ \begin{align*} V(s) & :=R(s)+\gamma \max _{a} \int_{s^{\prime}} P_{s a}\left(s^{\prime}\right) V\left(s^{\prime}\right) d s^{\prime} \tag{6}\\ &=R(s)+\gamma \max _{a} \mathrm{E}_{s^{\prime} \sim P a}\left[V\left(s^{\prime}\right)\right] \tag{7}\end{align*} \]
注意这里对于连续值需使用积分。拟合值迭代的主要思想就是:基于有限的状态样本 \(s^{(1)}, \ldots, s^{(m)}\) 对上述过程进行估计。
具体来说,我们会使用一个监督学习算法(线性回归),将值函数用状态的线性或非线性函数估计:
\[ V(s)=\theta^{T} \phi(s) \]
其中 \(\phi\) 是状态的某种适当的特征映射。
对于 \(m\) 个有限状态样本中的每一个状态 \(s\),拟合值迭代会先计算一个量 \(y^{(i)}\),作为对 \(R(s)+\gamma \max _{a} \mathrm{E}_{s^{\prime} \sim P a}\left[V\left(s^{\prime}\right)\right]\) 的估计,然后使用监督学习算法尝试去让 \(V(s)\) 接近 \(R(s)+\gamma \max _{a} \mathrm{E}_{s^{\prime} \sim P a}\left[V\left(s^{\prime}\right)\right]\)(即接近 \(y^{(i)}\)),从而学习出参数 \(\theta\)。
具体来说,算法的过程如下:
- 随机采样 \(m\) 个状态 \(s^{(1)}, s^{(2)}, \ldots s^{(m)} \in S\)
- 初始化 \(\theta := 0\)
- 重复下述过程:
- 对于 \(i=1, \ldots, m\)
- 对于每个动作 \(a \in A\),基于上述模型(模拟器)采样 \(s_{1}^{\prime}, \ldots, s_{k}^{\prime} \sim P_{s^{(i)} a}\);再令 \(q(a)=\frac{1}{k} \sum_{j=1}^{k} R\left(s^{(i)}\right)+\gamma V\left(s_{j}^{\prime}\right)\),这样 \(q(a)\) 就可以看做 \(R\left(s^{(i)}\right)+\gamma \mathrm{E}_{s^{\prime} \sim P_{s^{(i)}{a}}}\left[V\left(s^{\prime}\right)\right]\) 的估计
- 令 \(y^{(i)}=\max _{a} q(a)\),这样 \(y^{(i)}\) 可以看做 \(R\left(s^{(i)}\right)+\gamma \max _{a} \mathrm{E}_{s^{\prime} \sim P_{s^{(i)}{a}}}\left[V\left(s^{\prime}\right)\right]\) 的估计
- 对于每个动作 \(a \in A\),基于上述模型(模拟器)采样 \(s_{1}^{\prime}, \ldots, s_{k}^{\prime} \sim P_{s^{(i)} a}\);再令 \(q(a)=\frac{1}{k} \sum_{j=1}^{k} R\left(s^{(i)}\right)+\gamma V\left(s_{j}^{\prime}\right)\),这样 \(q(a)\) 就可以看做 \(R\left(s^{(i)}\right)+\gamma \mathrm{E}_{s^{\prime} \sim P_{s^{(i)}{a}}}\left[V\left(s^{\prime}\right)\right]\) 的估计
- 在原始的值迭代(离散值)中,我们需要更新 \(V\left(s^{(i)}\right) :=y^{(i)}\)。在本算法中,我们希望 \(V\left(s^{(i)}\right) \approx y^{(i)}\),使用监督学习算法:
\[ \operatorname{Set} \theta :=\arg \min _{\theta} \frac{1}{2} \sum_{i=1}^{m}\left(\theta^{T} \phi\left(s^{(i)}\right)-y^{(i)}\right)^{2} \]
上述算法使用了线性回归,实际上其他的回归算法也可以使用,如加权线性回归。
与离散状态集的值迭代不同,拟合值迭代并不一定总是会收敛。不过在实际应用中,其通常会收敛(或近似收敛)。需要注意的是,如果我们使用决定性模型(模拟器),那么算法中 \(k = 1\),因为下一个状态只有一个确定的值;否则我们需要取 \(k\) 个样本并求均值(即随机模型)。
最终,拟合值迭代输出 \(V\),其为对 \(V^{\star}\) 的估计。由于状态集连续,所以我们无法直接给出针对所有状态的完整最优策略,而是根据特定的状态选择特定的动作。当系统处于状态 \(s\) 时,可以通过下面的公式来选择动作:
\[ \arg \max _{a} \mathrm{E}_{s^{\prime} \sim P_{s a}}\left[V\left(s^{\prime}\right)\right] \]
上式计算的过程与算法的内循环类似,对于每一个动作,我们采样 \(s_{1}^{\prime}, \ldots, s_{k}^{\prime} \sim P_{s a}\),类似地,如果使用决定性模型,则 \(k=1\)。
在实际应用中,还有其他方法来估计上述值,例如:如果模拟器的形式为 \(s_{t+1} = f\left(s_{t}, a_{t}\right)+\epsilon_{t}\),其中 \(f\) 是某个决定性函数(如 \(f\left(s_{t}, a_{t}\right)=A s_{t}+B a_{t}\)),\(\epsilon\) 是 0 均值高斯噪声,则可以通过下述公式选择动作:
\[ \arg \max _{a} V(f(s, a)) \]
可以理解为令 \(\epsilon_t = 0\)(忽略模拟器中的噪声)及 \(k=1\)。我们也可以通过下述公式推导: \[ \begin{aligned} \mathrm{E}_{s^{\prime}}\left[V\left(s^{\prime}\right)\right] & \approx V\left(\mathrm{E}_{s^{\prime}}\left[s^{\prime}\right]\right) \\ &=V(f(s, a)) \end{aligned} \]
其中期望是针对 \(s^{\prime} \sim P_{s a}\) 的。第一步可以参考 Jensen 不等式(只要噪声项很小,则估计一般合理)。对于无法使用上述估计方法的问题,则可能需要采样 \(k|A|\) 个样本,这通常计算量较大。
思维导图
