CS229 学习笔记之十六：LQR, DDP 和 LQG

发表于 2019-07-09 分类于人工智能，课程笔记阅读次数：本文字数： 4.9k 阅读时长 ≈ 16 分钟

本篇博客为 CS229 学习笔记第十六部分，主题是：强化学习中的各种算法。

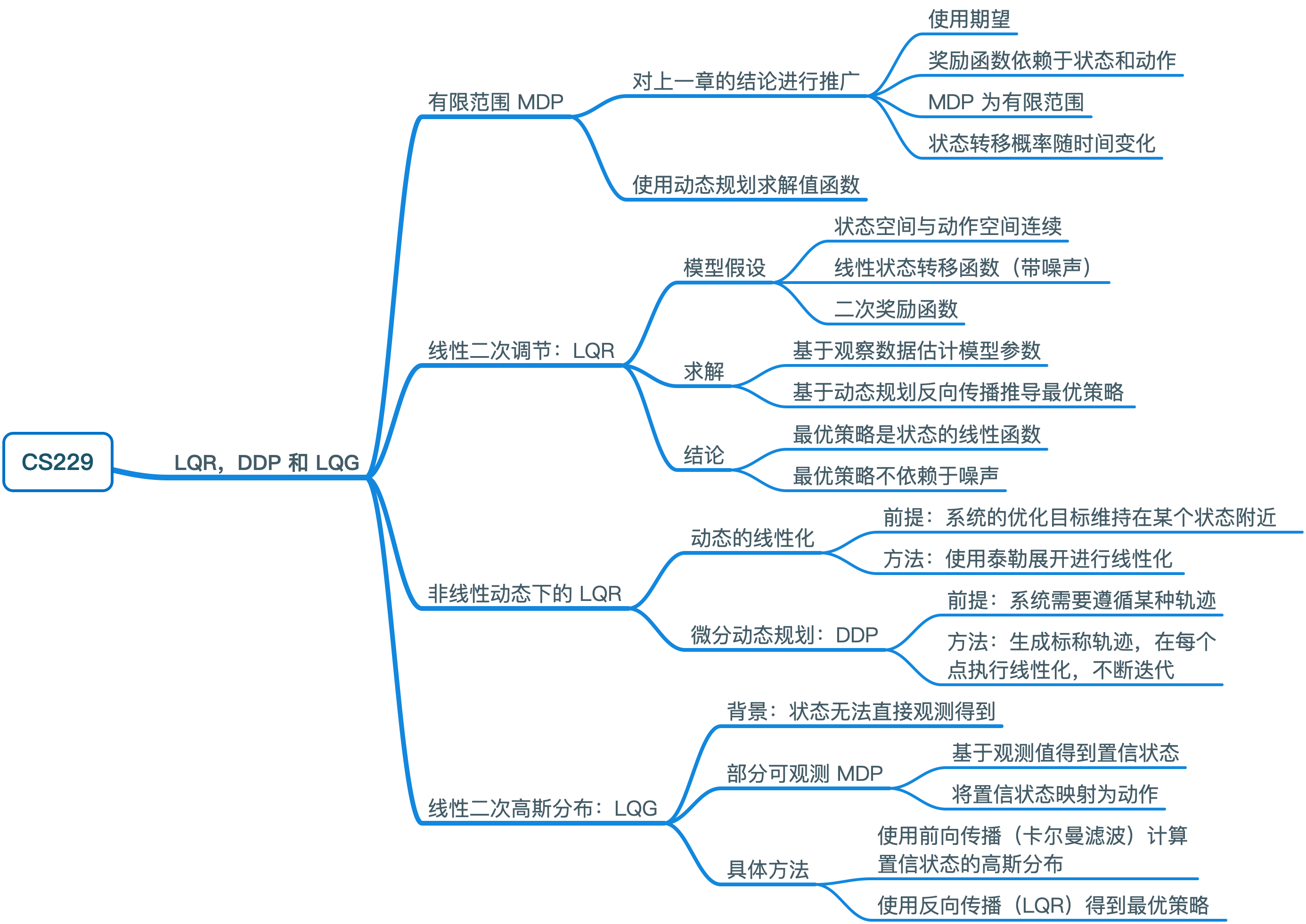
有限范围 MDP

在上一章中我们介绍了马尔可夫决策过程，其中最优贝尔曼公式给出了最优值函数的求解方法：

\[ V^{\pi^{*}}(s)=R(s)+\max _{a \in \mathcal{A}} \gamma \sum_{s^{\prime} \in S} P_{s a}\left(s^{\prime}\right) V^{\pi^{*}}\left(s^{\prime}\right) \] 根据最优值函数，我们还可以求解出最优策略： \[ \pi^{*}(s)=\operatorname{argmax}_{a \in \mathcal{A}} \sum_{s^{\prime} \in \mathcal{S}} P_{s a}\left(s^{\prime}\right) V^{*}\left(s^{\prime}\right) \] 在本章中，我们将对上一章的结论进行推广：

我们希望写出的方程对离散和连续情况均适用，即： \[ \begin{array}{c}{\mathbb{E}_{s^{\prime} \sim P_{s a}}\left[V^{\pi^{*}}\left(s^{\prime}\right)\right] \quad \text { instead of }} \\ {\sum_{s^{\prime} \in S} P_{s a}\left(s^{\prime}\right) V^{\pi^{*}}\left(s^{\prime}\right)}\end{array} \]
我们将假设奖励函数同时依赖于状态和动作，即 \(R : \mathcal{S} \times \mathcal{A} \rightarrow \mathbb{R}\)，这使得最优策略的计算公式变为： \[ \pi^{*}(s)=\operatorname{argmax}_{a \in \mathcal{A}} R(s, a)+\gamma \mathbb{E}_{s^{\prime} \sim P_{sa}}\left[V^{\pi^{*}}\left(s^{\prime}\right)\right] \]
不同于之前的无限范围，我们将假设 MDP 为有限范围，定义如下五元组： \[ \left(\mathcal{S}, \mathcal{A}, P_{s a}, T, R\right) \]

其中 \(T>0\) 为时间范围。在这样的设定中，对于收益的定义将发生变化： \[ R\left(s_{0}, a_{0}\right)+R\left(s_{1}, a_{1}\right)+\cdots+R\left(s_{T}, a_{T}\right) \]

而不是： \[ \begin{array}{l}{R\left(s_{0}, a_{0}\right)+\gamma R\left(s_{1}, a_{1}\right)+\gamma^{2} R\left(s_{2}, a_{2}\right)+\ldots} \\ {\sum_{t=0}^{\infty} R\left(s_{t}, a_{t}\right) \gamma^{t}}\end{array} \] 折扣因子的存在本质上是为了保证无限和的奖励函数为有限值。假设奖励函数的上界为某一常数 \(\bar{R}\)，则收益为：

\[ \left|\sum_{t=0}^{\infty} R\left(s_{t}\right) \gamma^{t}\right| \leq \overline{R} \sum_{t=0}^{\infty} \gamma^{t} \] 其为一个几何级数和（有限和），因为这里收益本身即为有限和，所以折扣因子也不再需要。

此外，在有限范围下，最优策略 \(\pi^{\star}\) 将不稳定，随时间发生变化： \[ \pi^{(t)} : \mathcal{S} \rightarrow \mathcal{A} \]

这种情况出现的原因从直观上可以理解为：我们希望基于处于环境中的位置与剩余的时间来采取不同的策略。
我们将使用基于时间的动态方法： \[ s_{t+1} \sim P_{s_{t}, a_{t}}^{(t)} \]

即状态转移概率随时间变化。奖励函数同样随时间变化 \(R^{(t)}\)，这样的设定更加符合实际情况。结合之前的设定，有限范围 MDP 的通用公式如下：

\[ \left(\mathcal{S}, \mathcal{A}, P_{s a}^{(t)}, T, R^{(t)}\right) \]

注：上述方程与在状态中加入时间等价。

时间 \(t\) 的值函数（使用策略 \(\pi\)）使用与之前相同的方式定义： \[ V_{t}(s)=\mathbb{E}\left[R^{(t)}\left(s_{t}, a_{t}\right)+\cdots+R^{(T)}\left(s_{T}, a_{T}\right) | s_{t}=s, \pi\right] \]

现在的问题是，如何在有限范围下找出最优值函数： \[ V_{t}^{*}(s)=\max _{\pi} V_{t}^{\pi}(s) \]

我们可以用动态规划的思想来求解这一问题：

在决策过程的最后，最优值函数为： \[ \forall s \in \mathcal{S} : \quad V_{T}^{*}(s) :=\max _{a \in \mathcal{A}} R^{(T)}(s, a) \tag{1} \]
对于其他时间步 \(0 \leq t < T\)，如果已知下一个时间步的最优值函数 \(V_{t+1}^{*}\)，则： \[ \forall t < T, s \in \mathcal{S} : \quad V_{t}^{*}(s) :=\max _{a \in \mathcal{A}}\left[R^{(t)}(s, a)+\mathbb{E}_{s^{\prime} \sim P_{s a}^{(t)}}\left[V_{t+1}^{*}\left(s^{\prime}\right)\right]\right] \tag{2} \]

基于上述观察，可以用如下算法来求解最优值函数：

使用 \((1)\) 式计算 \(V_{T}^{*}\)
对于 \(t=T-1, \dots, 0\)，使用 \((2)\) 式基于 \(V_{t+1}^{*}\) 计算 \(V_{t}^{*}\)

实际上，我们可以将标准的值迭代看做上述算法的特例（不追踪时间），如果在标准设置下，运行值迭代 \(T\) 次，则可以得到最优值迭代的 \(\gamma^T\) 估计（几何收敛）。我们还可以证明如下定理：

定理：令 \(B\) 定义贝尔曼更新以及 \(\|f(x)\|_{\infty} :=\sup _{x}|f(x)|\) （上界）。如果 \(V_t\) 表示 \(t\) 时间步的值函数，则有： \[ \begin{aligned}\left\|V_{t+1}-V^{*}\right\|_{\infty} &=\left\|B\left(V_{t}\right)-V^{*}\right\|_{\infty} \\ & \leq \gamma\left\|V_{t}-V^{*}\right\|_{\infty} \\ & \leq \gamma^{t}\left\|V_{1}-V^{*}\right\|_{\infty} \end{aligned} \] 可以看出，贝尔曼更新 \(B\) 是一个 \(\gamma\) 收缩算子。

线性二次调节（LQR）

本节我们将介绍有限范围 MDP 下的一个特例：LQR 模型。通过该模型我们可以求得精确的解。该模型常用于机器人控制，很多问题经常将问题简化成该模型。

首先定义模型假设：

假设一：状态空间与动作空间连续： \[ \mathcal{S}=\mathbb{R}^{n}, \;\;\mathcal{A}=\mathbb{R}^{d} \] 假设二：线性转移函数（带噪声）： \[ s_{t+1}=A_{t} s_{t}+B_{t} a_{t}+w_{t} \]

其中 \(A_{t} \in R^{n \times n}, B_{t} \in R^{n \times d}\) 为矩阵，\(w_{t} \sim \mathcal{N}\left(0, \Sigma_{t}\right)\) 为某个高斯噪声（0 均值），之后我们会证明最优策略与噪声无关！

假设三：二次奖励函数： \[ R^{(t)}\left(s_{t}, a_{t}\right)=-s_{t}^{\top} U_{t} s_{t}-a_{t}^{\top} W_{t} a_{t} \]

其中 \(U_{t} \in R^{n \times n}, W_{t} \in R^{d \times d}\) 为正定矩阵，这意味着奖励函数一直为负。该奖励函数的特征表明我们希望状态接近原点（小范数），可以理解为模型希望维持稳定，避免过度的波动。

定义完假设后，下面介绍 LQR 算法的两个步骤：

Step 1：假定 \(A, B, \Sigma\) 未知，我们需要基于观察数据进行估计。

对于 \(A,B\)，使用值函数近似章节中的方法进行估计： \[ \operatorname{argmin}_{A, B} \sum_{i=1}^{m} \sum_{t=0}^{T-1}\left\|s_{t+1}^{(i)}-\left(A s_{t}^{(i)}+B a_{t}^{(i)}\right)\right\|^{2} \]
对于 \(\Sigma\)，使用高斯判别分析方法进行估计（极大似然）

Step 2：假定模型参数已知（给定或估计得出），我们可以使用动态规划算法来推导最优策略，即给定： \[ \left\{\begin{array}{ll}{s_{t+1}} & {=A_{t} s_{t}+B_{t} a_{t}+w_{t} \quad A_{t}, B_{t}, U_{t}, W_{t}, \Sigma_{t} \text { known }} \\ {R^{(t)}\left(s_{t}, a_{t}\right)} & {=-s_{t}^{\top} U_{t} s_{t}-a_{t}^{\top} W_{t} a_{t}}\end{array}\right. \] 我们希望去计算 \(V_{t}^{*}\)。使用第一节中提到的动态规划方法，我们有：

初始化步骤

对于最后一个时间步 \(T\)： \[ \begin{aligned} V_{T}^{*}\left(s_{T}\right) &=\max _{a_{F} \in \mathcal{A}} R_{T}\left(s_{T}, a_{T}\right) \\ &=\max _{a_{T} \in \mathcal{A}}-s_{T}^{\top} U_{T} s_{T}-a_{T}^{\top} W_{T} a_{T} \\ &=-s_{T}^{\top} U_{T} s_{T} & \text { (maximized for } a_{T}=0 ) \end{aligned} \]
循环步骤

令 \(t < T\)，假定我们已知 \(V_{t+1}^{*}\)。

事实 1：如果 \(V_{t+1}^{*}\) 是一个二次函数，那么 \(V_{t}^{*}\) 也是一个二次函数，即： \[ \begin{aligned} \text { if } V_{t+1}^{*}\left(s_{t+1}\right) &=s_{t+1}^{\top} \Phi_{t+1} s_{t+1}+\Psi_{t+1} \\ \text { then } V_{t}^{*}\left(s_{t}\right) &=s_{t}^{\top} \Phi_{t} s_{t}+\Psi_{t} \end{aligned} \]

对于时间步 \(t=T\)，我们有 \(\Phi_{t}=-U_{T}\) 以及 \(\Psi_{T}=0\)（根据初始化步骤中的结论）。

事实 2：我们可以证明最优策略是状态的线性函数。

知道了 \(V_{t+1}^{*}\) 就等同于知道了 \(\Phi_{t+1}\) 和 \(\Psi_{t+1}\)，我们只需要解释如何基于 \(\Phi_{t+1}\) 和 \(\Psi_{t+1}\) 以及其他参数来计算 \(\Phi_{t}\) 和 \(\Psi_{t}\)。根据最优值函数的定义以及模型假设，我们有：

\[ \begin{aligned} V_{t}^{*}\left(s_{t}\right) &=s_{t}^{\top} \Phi_{t} s_{t}+\Psi_{t} \\ &=\max _{a_{t}}\left[R^{(t)}\left(s_{t}, a_{t}\right)+\mathbb{E}_{s_{t+1} \sim P_{s_t,a_t}^{(t)}}\left[V_{t+1}^{*}\left(s_{t+1}\right)\right]\right] \\ &=\max _{a_{t}}\left[-s_{t}^{\top} U_{t} s_{t}-a_{t}^{\top} V_{t} a_{t}+\mathbb{E}_{s_{t+1} \sim \mathcal{N}\left(A_{t} s_{t}+B_{t} a_{t}, \Sigma_{t}\right)}\left[s_{t+1}^{\top} \Phi_{t+1} s_{t+1}+\Psi_{t+1}\right]\right] \end{aligned} \]

上式可以优化为关于 \(a_t\) 的二次函数（过程省略o(╯□╰)o），我们可以解得最优动作 \(a_{t}^{*}\)： \[ \begin{aligned} a_{t}^{*} &=\left[\left(B_{t}^{\top} \Phi_{t+1} B_{t}-V_{t}\right)^{-1} B_{t} \Phi_{t+1} A_{t}\right] \cdot s_{t} \\ &=L_{t} \cdot s_{t} \end{aligned} \]

其中： \[ L_{t} :=\left[\left(B_{t}^{\top} \Phi_{t+1} B_{t}-W_{t}\right)^{-1} B_{t} \Phi_{t+1} A_{t}\right] \] 根据上式可以得出：最优策略与 \(s_t\) 线性相关。给定 \(a_{t}^{*}\) 我们可以求解 \(\Phi_{t}\) 和 \(\Psi_{t}\)，得出离散里卡蒂方程： \[ \begin{aligned} \Phi_{t} &=A_{t}^{\top}\left(\Phi_{t+1}-\Phi_{t+1} B_{t}\left(B_{t}^{\top} \Phi_{t+1} B_{t}-W_{t}\right)^{-1} B_{t} \Phi_{t+1}\right) A_{t}-U_{t} \\ \Psi_{t} &=-\operatorname{tr}\left(\Sigma_{t} \Phi_{t+1}\right)+\Psi_{t+1} \end{aligned} \] 事实 3：可以看到 \(\Phi_{t}\) 不依赖于 \(\Psi\) 和噪声 \(\Sigma_t\)，这表明最优策略也不依赖于噪声！（但是 \(\Psi_t\) 依赖于 \(\Sigma_t\)，即 \(V_{t}^{*}\) 也依赖于 \(\Sigma_t\)）

最后进行总结，LQR 算法的流程如下：

估计参数 \(A_{t}, B_{t}, \Sigma_{t}\) （如果必要）
初始化 \(\Phi_{T} :=-U_{T}\) 和 \(\Psi_{T} :=0\)
从 \(t=T-1 \ldots 0\) 开始迭代更新 \(\Phi_{t}\) 和 \(\Psi_{t}\)，使用离散里卡蒂方程（基于 \(\Phi_{t+1}\) 和 \(\Psi_{t+1}\)）。只要存在能朝 0 状态前进的策略，收敛性就可以得到保障
求解最优策略 \(a_{t}^{*} =\left[\left(B_{t}^{\top} \Phi_{t+1} B_{t}-V_{t}\right)^{-1} B_{t} \Phi_{t+1} A_{t}\right] \cdot s_{t}\)，注意因为最优策略不依赖于 \(\Psi_{t}\)，所以可以不更新

非线性动态下的 LQR

对于很多问题，即便其动态非线性，也可以化简为 LQR。例如，对于倒立摆问题，其状态间的转换关系为：

\[ \left(\begin{array}{c}{x_{t+1}} \\ {\dot{x}_{t+1}} \\ {\theta_{t+1}} \\ {\dot{\theta}_{t+1}}\end{array}\right)=F\left(\left(\begin{array}{c}{x_{t}} \\ {\dot{x}_{t}} \\ {\theta_{t}} \\ {\dot{\theta}_{t}}\end{array}\right), a_{t}\right) \]

其中函数 \(F\) 取决于角度的余弦。我们的问题是：该系统能够线性化吗？

动态的线性化

假定在时间 \(t\)，系统大部分时间都处于状态 \(\bar{s_t}\)，且选取的行为在 \(\bar{a_t}\) 附近。对于倒立摆问题，如果我们达到了某种最优状态，就会满足：行为空间很小且和竖直方向的偏差不大。

我们可以使用泰勒展开来进行线性化。先考虑最简单的情况：状态为一维且转换函数 \(F\) 不依赖于动作，则我们可以写出：

\[ s_{t+1}=F\left(s_{t}\right) \approx F\left(\bar{s_{t}}\right)+F^{\prime}\left(\bar{s_{t}}\right) \cdot\left(s_{t}-\bar{s_{t}}\right) \] 对于更一般的情况，公式看上去基本一样，只是将简单的导数换成了梯度： \[ s_{t+1} \approx F\left(\bar{s_{t}}, \bar{a_{t}}\right)+\nabla_{s} F\left(\bar{s_{t}}, \bar{a_{t}}\right) \cdot\left(s_{t}-\bar{s_{t}}\right)+\nabla_{a} F\left(\bar{s_{t}}, \bar{a_{t}}\right) \cdot\left(a_{t}-\bar{a_{t}}\right) \tag{3} \] 现在我们可以重写 \((3)\) 式来得到如下线性关系： \[ s_{t+1} \approx A s_{t}+B a_{t}+\kappa \]

其中 \(\kappa\) 是某个常数，\(A,B\) 是矩阵。我们可以通过将常数项合并到 \(s_t\) 中（增加一维）使得公式的形式与之前一致。

微分动态规划（DDP）

之前所说的方法适用于优化目标为保持在某个状态 \(s^{\star}\) 附近，如倒立摆、无人驾驶（保持在路中间）等。而某些情况下，目标往往更加复杂。下面介绍一种方法，其适用于系统需要遵循某种轨迹（比如火箭）。该方法将轨迹离散化为离散的时间步，并创造中间目标来使用之前的方法。这种方法称为微分动态规划，其主要步骤如下：

Step 1：使用一个简单的控制器得到一条标称轨迹，作为对目标轨迹的估计： \[ s_{0}^{*}, a_{0}^{*} \rightarrow s_{1}^{*}, a_{1}^{*} \rightarrow \ldots \] Step 2：在每个轨迹点 \(s_{t}^{*}\) 执行线性化： \[ s_{t+1} \approx F\left(s_{t}^{*}, a_{t}^{*}\right)+\nabla_{s} F\left(s_{t}^{*}, a_{t}^{*}\right)\left(s_{t}-s_{t}^{*}\right)+\nabla_{a} F\left(s_{t}^{*}, a_{t}^{*}\right)\left(a_{t}-a_{t}^{*}\right) \]

其中 \(s_t,a_t\) 表示当前的状态和动作。现在我们可以使用之前的方法，将上式重写为： \[ s_{t+1}=A_{t} \cdot s_{t}+B_{t} \cdot a_{t} \]

注意这里使用的是非平稳动态设定，即策略随时间发生变化。

类似地，我们可以通过二阶泰勒展开得到奖励函数 \(R^{(t)}\)： \[ \begin{aligned} R\left(s_{t}, a_{t}\right) & \approx R\left(s_{t}^{*}, a_{t}^{*}\right)+\nabla_{s} R\left(s_{t}^{*}, a_{t}^{*}\right)\left(s_{t}-s_{t}^{*}\right)+\nabla_{a} R\left(s_{t}^{*}, a_{t}^{*}\right)\left(a_{t}-a_{t}^{*}\right) \\ &+\frac{1}{2}\left(s_{t}-s_{t}^{*}\right)^{\top} H_{s s}\left(s_{t}-s_{t}^{*}\right)+\left(s_{t}-s_{t}^{*}\right)^{\top} H_{s a}\left(a_{t}-a_{t}^{*}\right) \\ &+\frac{1}{2}\left(a_{t}-a_{t}^{*}\right)^{\top} H_{a a}\left(a_{t}-a_{t}^{*}\right) \end{aligned} \]

其中 \(H_{xy}\) 表示 \(R\) 的海森矩阵项。上式可以重写为（使用之前所述的增加维度技巧）： \[ R_{t}\left(s_{t}, a_{t}\right)=-s_{t}^{\top} U_{t} s_{t}-a_{t}^{\top} W_{t} a_{t} \]

如果想自己证明，注意下式： \[ \left(\begin{array}{ll}{1} & {x}\end{array}\right) \cdot\left(\begin{array}{ll}{a} & {b} \\ {b} & {c}\end{array}\right) \cdot\left(\begin{array}{l}{1} \\ {x}\end{array}\right)=a+2 b x+c x^{2} \] Step 3：现在，我们已经将问题严格地重写为了 LQR 框架下的形式，可以使用 LQR 来找到最优策略 \(\pi_t\)。

注意：如果 LQR 轨迹（下一步）与轨迹的线性近似偏离过多，可能会出现问题，需要通过调节奖励函数的形态来修正。

Step 4：现在我们得到了新的控制器（新策略 \(\pi_t\)），我们将构建一个新的轨迹： \[ s_{0}^{*}, \pi_{0}\left(s_{0}^{*}\right) \rightarrow s_{1}^{*}, \pi_{1}\left(s_{1}^{*}\right) \rightarrow \rightarrow s_{T}^{*} \]

注意生成新轨迹时，我们使用真实的函数 \(F\) 而不是其线性估计来计算转换，即： \[ s_{t+1}^{*}=F\left(s_{t}^{*}, a_{t}^{*}\right) \] 然后返回步骤 2，进行重复直到满足某些停止条件。

线性二次高斯分布（LQG）

目前为止，我们假设状态都是可以得到的，而在现实世界中，实际的观测值可能并不是真实的状态值（类似 HMM）。我们将使用部分可观测 MDP（POMDP）来解决这类问题。

POMDP 是一种包含额外观察层的 MDP。我们将引入一个新的变量 \(o_t\)，其满足某种条件概率分布： \[ o_{t}\left|s_{t} \sim O(o | s)\right. \] 形式上看，一个有限范围 POMDP 由如下六元组给出： \[ \left(\mathcal{S}, \mathcal{O}, \mathcal{A}, P_{s a}, T, R\right) \] 在该框架下，一种通用的策略是先基于观测值 \(o_1,\ldots,o_t\) 得到一个置信状态，然后 POMDP 的策略将置信状态映射为动作。

本节我们将对 LQR 进行拓展来求解 POMDP，假定我们观测到 \(y_{t} \in \mathbb{R}^{m}\)（\(m < n\)），并满足： \[ \left\{\begin{array}{ll}{y_{t}} & {=C \cdot s_{t}+v_{t}} \\ {s_{t+1}} & {=A \cdot s_{t}+B \cdot a_{t}+w_{t}}\end{array}\right. \]

其中 \(C \in R^{m \times n}\) 为压缩矩阵，\(v_{t}\) 和 \(w_{t}\) 一样为高斯噪声；奖励函数保持不变，为状态（非观测值）和动作的函数；置信状态同样满足高斯分布。在上述设定下，具体的算法如下：

Step 1：基于观测值计算置信状态的高斯分布： \[ s_{t} | y_{1}, \ldots, y_{t} \sim \mathcal{N}\left(s_{t | t}, \Sigma_{t | t}\right) \]

我们希望计算均值 \(s_{t | t}\) 和协方差 \(\Sigma_{t | t}\)。我们将使用卡尔曼滤波算法来提升计算效率（之后介绍）。

Step 2：得到分布后，我们将使用均值 \(s_{t | t}\) 作为对 \(s_t\) 的最佳估计。

Step 3：选择动作 \(a_{t} :=L_{t} s_{t | t}\) 其中 \(L_t\) 来自常规的 LQR 算法。

直观上来看，因为 \(s_{t | t}\) 是 \(s_t\) 的噪声估计（相当于向 LQR 中添加更多噪声），而 LQR 是与噪声无关的，所以这个算法可以工作。

下面对第一步进行解释，这里我们假设状态与动作无关（\(A\) 和 \(C\) 可以基于观察数据估计）： \[ \left\{\begin{array}{ll}{s_{t+1}} & {=A \cdot s_{t}+w_{t}, \quad w_{t} \sim N\left(0, \Sigma_{s}\right)} \\ {y_{t}} & {=C \cdot s_{t}+v_{t}, \quad v_{t} \sim N\left(0, \Sigma_{y}\right)}\end{array}\right. \]

因为噪声是高斯分布，所以我们可以证明联合分布也为高斯分布： \[ \left(\begin{array}{c}{s_{1}} \\ {\vdots} \\ {s_{t}} \\ {y_{1}} \\ {\vdots} \\ {y_{t}}\end{array}\right) \sim \mathcal{N}(\mu, \Sigma) \qquad \text { for some } \mu, \Sigma \]

使用高斯分布的边缘公式（参考因子分析章节），我们可以得到： \[ s_{t} | y_{1}, \ldots, y_{t} \sim \mathcal{N}\left(s_{t | t}, \Sigma_{t | t}\right) \] 然而计算边缘分布的参数计算过于复杂，可能会达到 \(O(t^4)\) 的复杂度。我们将使用卡尔曼滤波算法来更快捷地计算均值与方差，仅需要常数时间 t。算法分为两步，假定我们已知分布 \(s_{t} | y_{1}, \dots, y_{t}\)：

预测步：计算 \(s_{t+1} | y_{1}, \dots, y_{t}\)
更新步：计算 \(s_{t+1} | y_{1}, \dots, y_{t+1}\)

不断迭代上述步骤，即可更新置信状态： \[ \left(s_{t} | y_{1}, \ldots, y_{t}\right) \stackrel{\text { predict }}{\longrightarrow}\left(s_{t+1} | y_{1}, \ldots, y_{t}\right) \stackrel{\text { update }}{\longrightarrow}\left(s_{t+1} | y_{1}, \ldots, y_{t+1}\right) \stackrel{\text { predict }}{\longrightarrow} \ldots \]

下面具体解释两个步骤：

预测步：假定我们已知分布： \[ s_{t} | y_{1}, \ldots, y_{t} \sim \mathcal{N}\left(s_{t | t}, \Sigma_{t | t}\right) \]

则下一个状态的分布也为高斯分布： \[ s_{t+1} | y_{1}, \ldots, y_{t} \sim \mathcal{N}\left(s_{t+1 | t}, \Sigma_{t+1 | t}\right) \] 其中： \[ \left\{\begin{array}{ll}{s_{t+1 | t}} & {=A \cdot s_{t | t}} \\ {\Sigma_{t+1 | t}} & {=A \cdot \Sigma_{t | t} \cdot A^{\top}+\Sigma_{s}}\end{array}\right. \] 更新步：给定 \(s_{t+1} | t\) 和 \(\Sigma_{t+1 | t}\)，我们可以证明： \[ s_{t+1} | y_{1}, \ldots, y_{t+1} \sim \mathcal{N}\left(s_{t+1 | t+1}, \Sigma_{t+1 | t+1}\right) \]

其中： \[ \left\{\begin{array}{ll}{s_{t+1 | t+1}} & {=s_{t+1 | t}+K_{t}\left(y_{t+1}-C s_{t+1 | t}\right)} \\ {\Sigma_{t+1 | t+1}} & {=\Sigma_{t+1 | t}-K_{t} \cdot C \cdot \Sigma_{t+1 | t}}\end{array}\right. \] 矩阵 \(K_t\) 也称为卡尔曼增益： \[ K_{t} :=\Sigma_{t+1 | t} C^{\top}\left(C \Sigma_{t+1 | t} C^{\top}+\Sigma_{y}\right)^{-1} \]

从公式可以看出我们并不需要时间步 t 之前的观测值，仅需要之前的概率分布。

将上述过程结合起来，算法的整体过程如下：

运行前向传播来计算 \(K_{t}\) ，\(\Sigma_{t | t}\) 和 \(s_{t|t}\)
运行反向传播（LQR 更新）来计算量 \(\Phi_t\)，\(\Psi_{t}\) 和 \(L_t\)
使用 \(a_{t}^{*}=L_{t} s_{t | t}\) 来得到最优策略