本体入门之二:OWL 本体构建指南
本篇博客介绍如何通过 Protege 构建 OWL 本体。
本文将介绍如何通过 Protege 构建 OWL 本体,文中使用的软件版本为 mac 上的 protege 5.5.0 桌面版。
OWL 本体简介
OWL 是由 W3C 开发的一种本体描述语言,按照表达性可以被分为三类:
- OWL-Lite:可表达性最低
- OWL-DL:可表达性中等(本指南使用)
- OWL-Full:可表达性最高
本指南中将使用 OWL-DL(下文简称为 OWL),其基于描述性逻辑(Description Logics),表达性适中且支持自动化推理。关于 OWL 版本的选择,可以参考如下准则:OWL-Lite 和 OWL-DL 间的选择主要取决于OWL-Lite 的简单结构是否足够;OWL-DL 和 OWL-Full 间的选择则取决于是否需要支持自动推理或是否需要使用复杂的表达或建模工具。
OWL 本体的组件与 Protege 框架下的本体组件相对应,包括:
- Individuals:对应 Instances
- Properties:对应 Slots
- Classes:对应 Classes
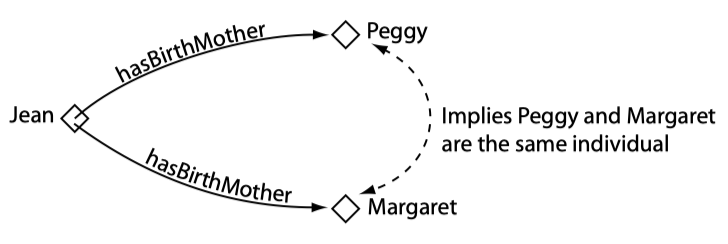
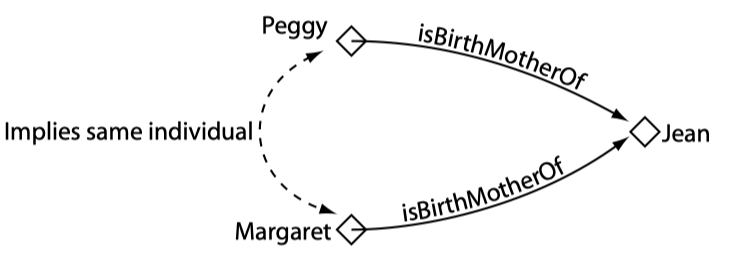
Individuals(个体)
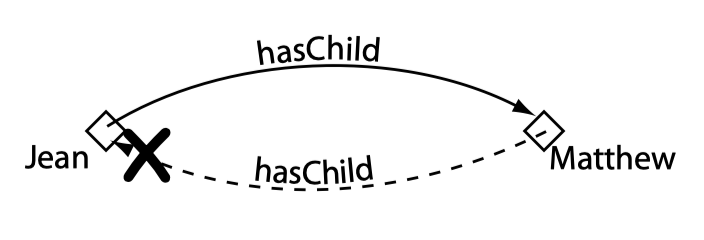
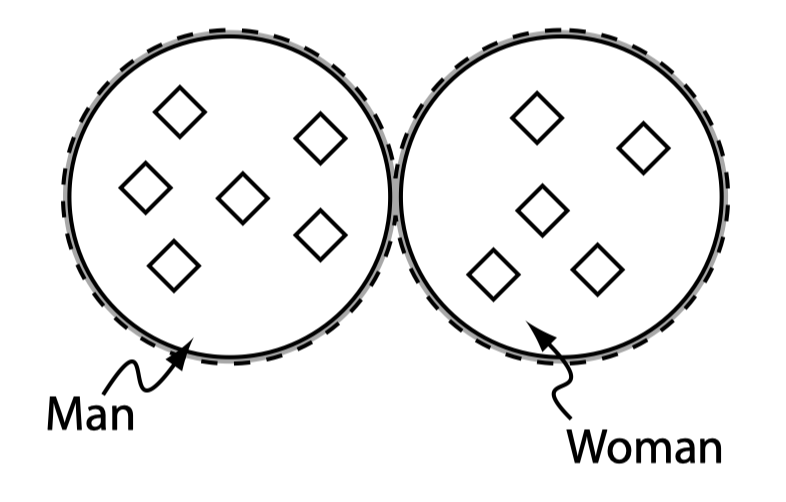
个体表示我们感兴趣的领域中的对象。与其他基于 Protege 的本体的重要区别在于,原始的 OWL 不遵循唯一命名假设(UNA),即两个不同名称的个体可能表示同一个个体,在 OWL 中,必须要明确指出个体之间是等同的还是不同的,否则其可能相同也可能不同。
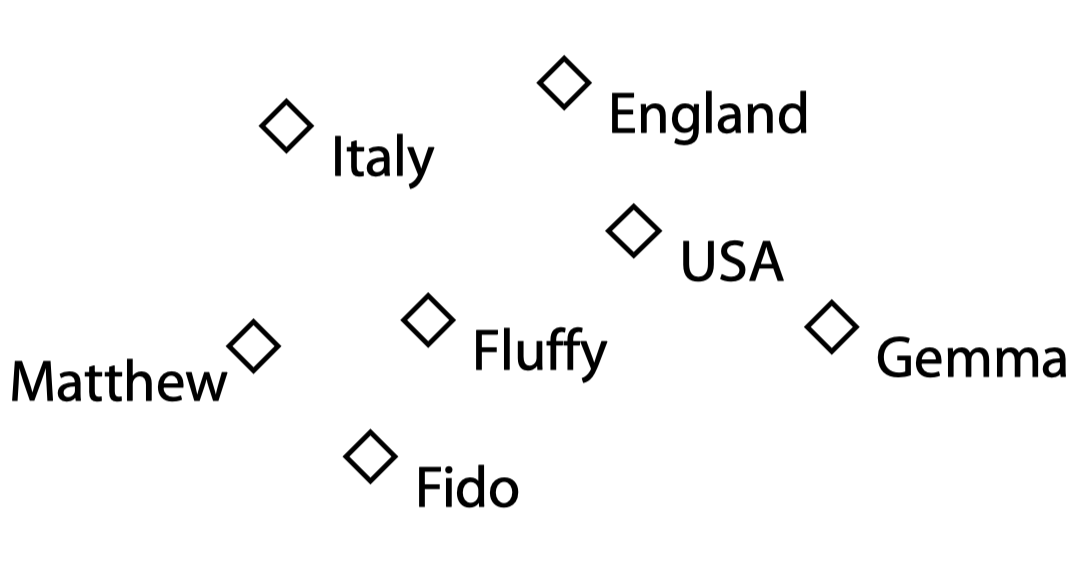
下图给出了对某个领域中某些个体的表示:
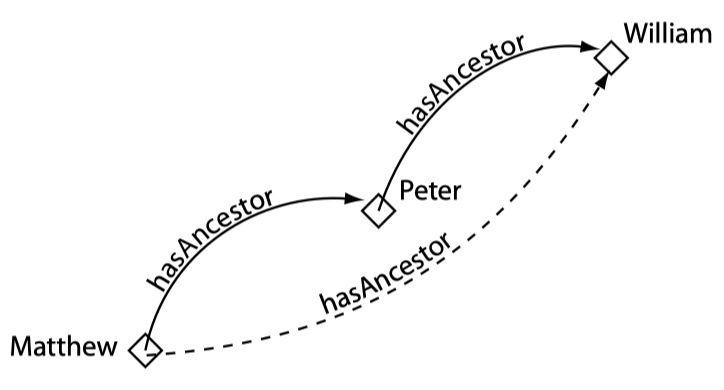
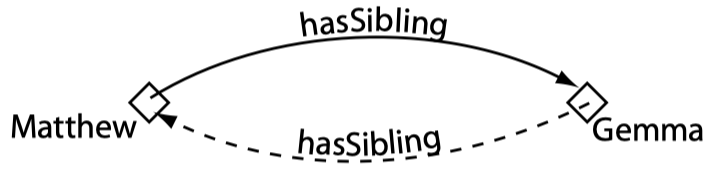
Properties(属性)
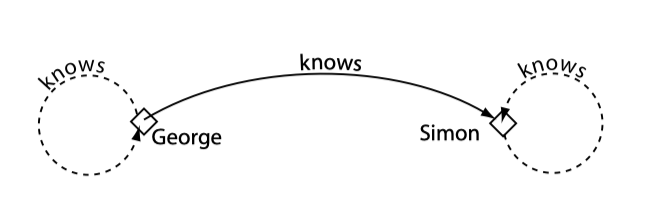
属性是个体间的二元关系,即属性将两个个体连接在一起。
属性拥有多种特征,如:
- 可以转置
- 可以被限制为单值
- 可以传递或具有对称性
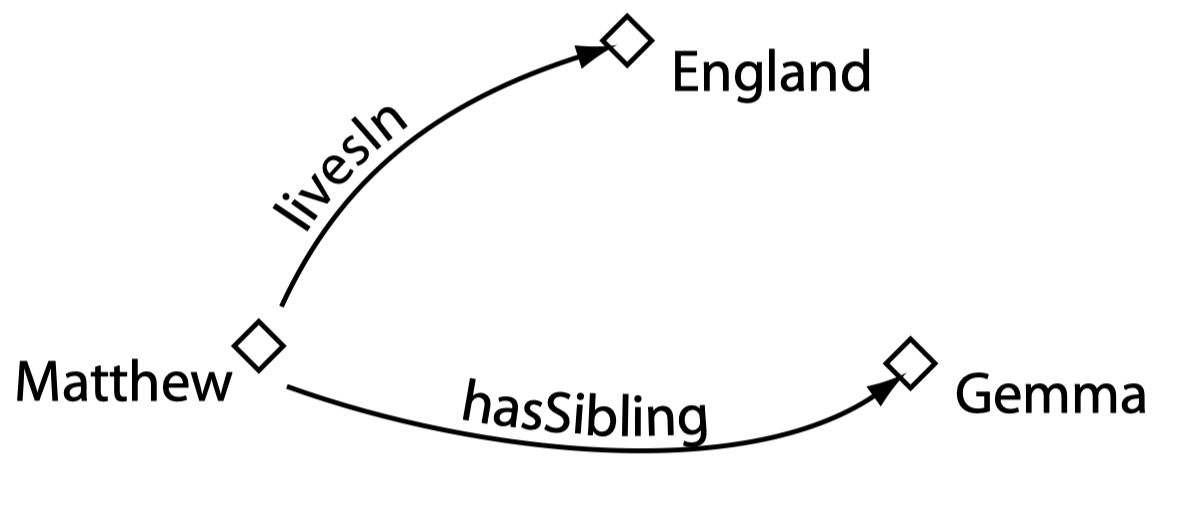
下图展示了将某些个体连接起来的某些属性:
Classes(类)
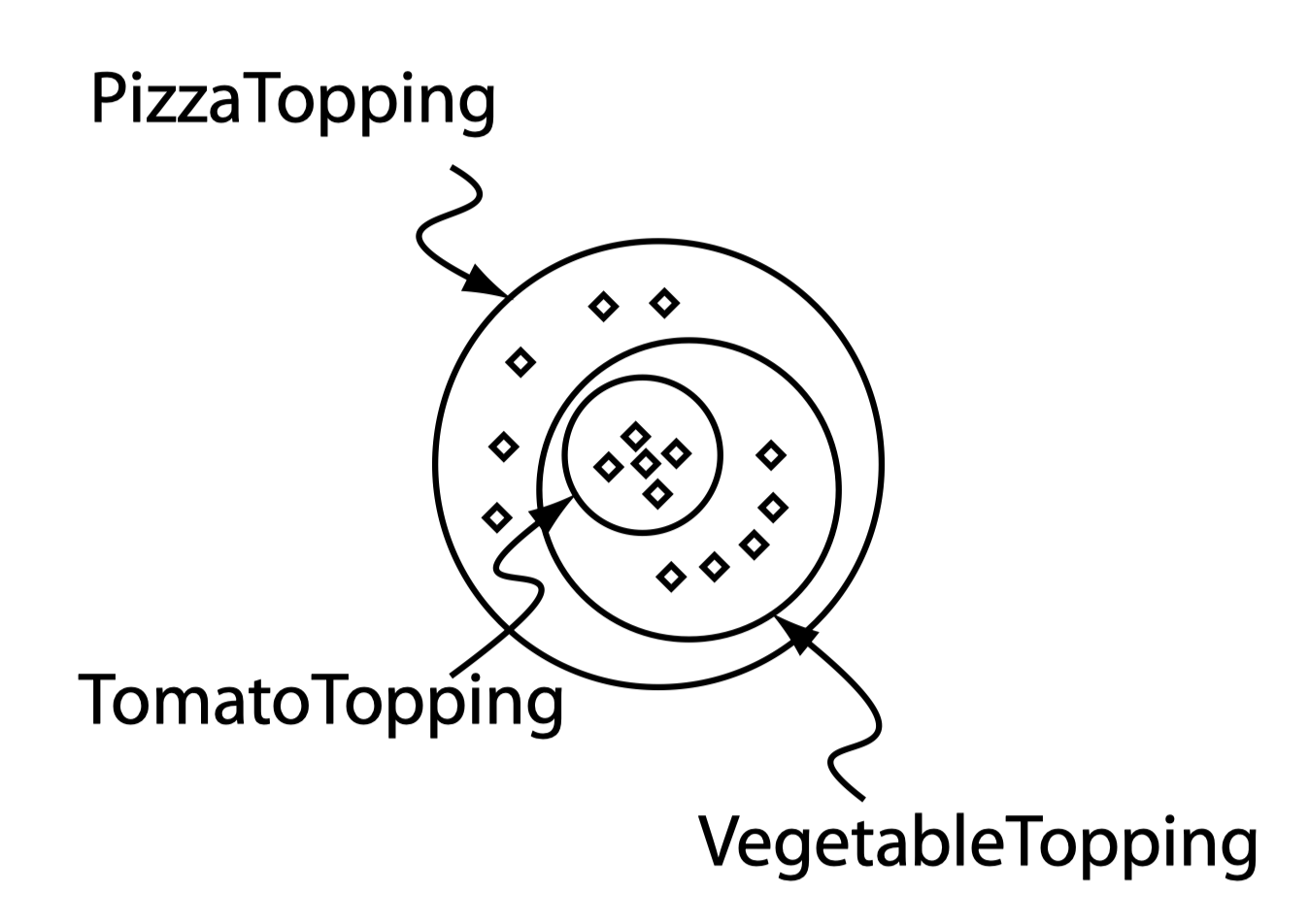
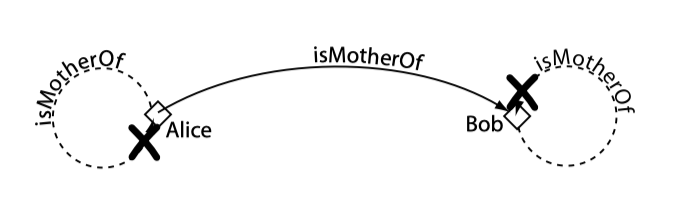
类可以理解为包含个体的集合。类通常使用正式的描述来精确表明其需求,如类 Cat 会包含领域中所有的猫的个体。类可以被组织为超类-子类的层级关系,即分类学(taxonomy)。OWL 的一个重要特征是超类-子类关系可以由推理机自动计算得出。
下图给出了包含个体的某些类:

构建一个 OWL 本体
本章节以创建一个披萨本体为例,介绍如何通过 protoge 构建一个 OWL 本体。
创建本体
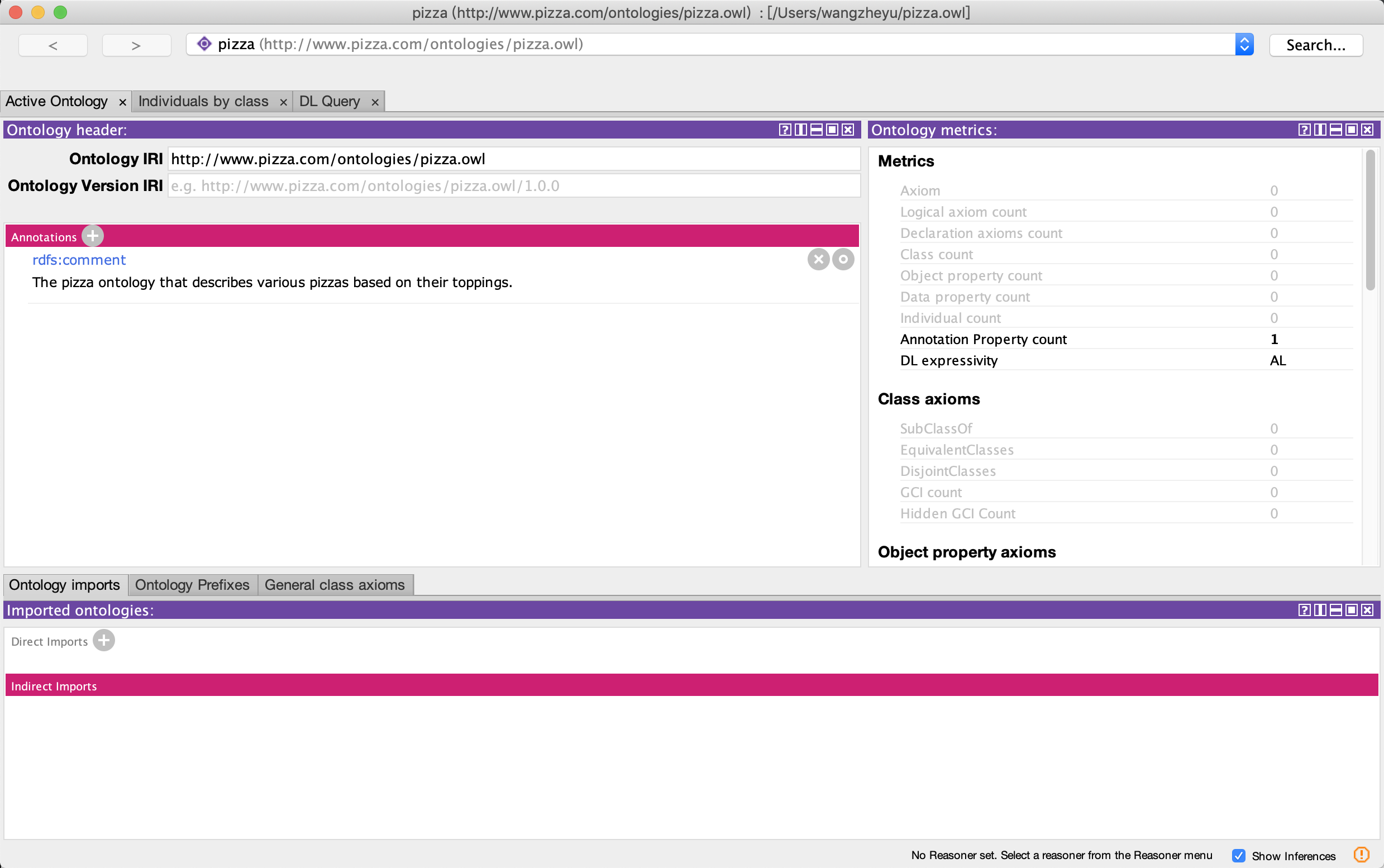
File -> New 新建一个本体,修改其 IRI(每个本体唯一):

以 OWL 形式保存为 "pizza.owl":
在 Annotation 中可以添加评论:
当前状态如下:
创建类
首先,在 Classes Tab 下(可能需要手动打开),新建 Thing 的子类。Thing 表示所有个体的集合。选中 Thing 后新建子类,新建一个子类后可以选择新建兄弟类:
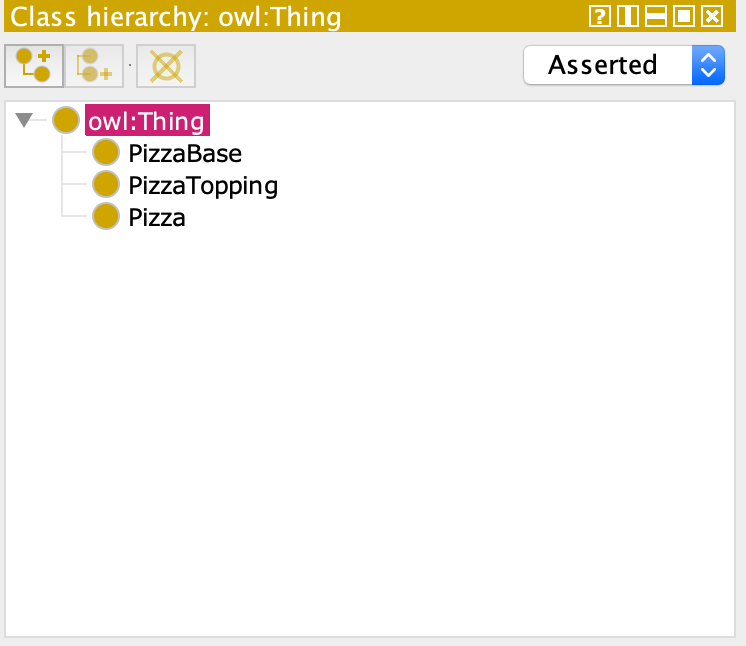
注意类的命名规则应该统一,建议使用驼峰命名。然后为这些子类设置 disjoint。disjoint 即一个类的实例无法归属于另一个类:

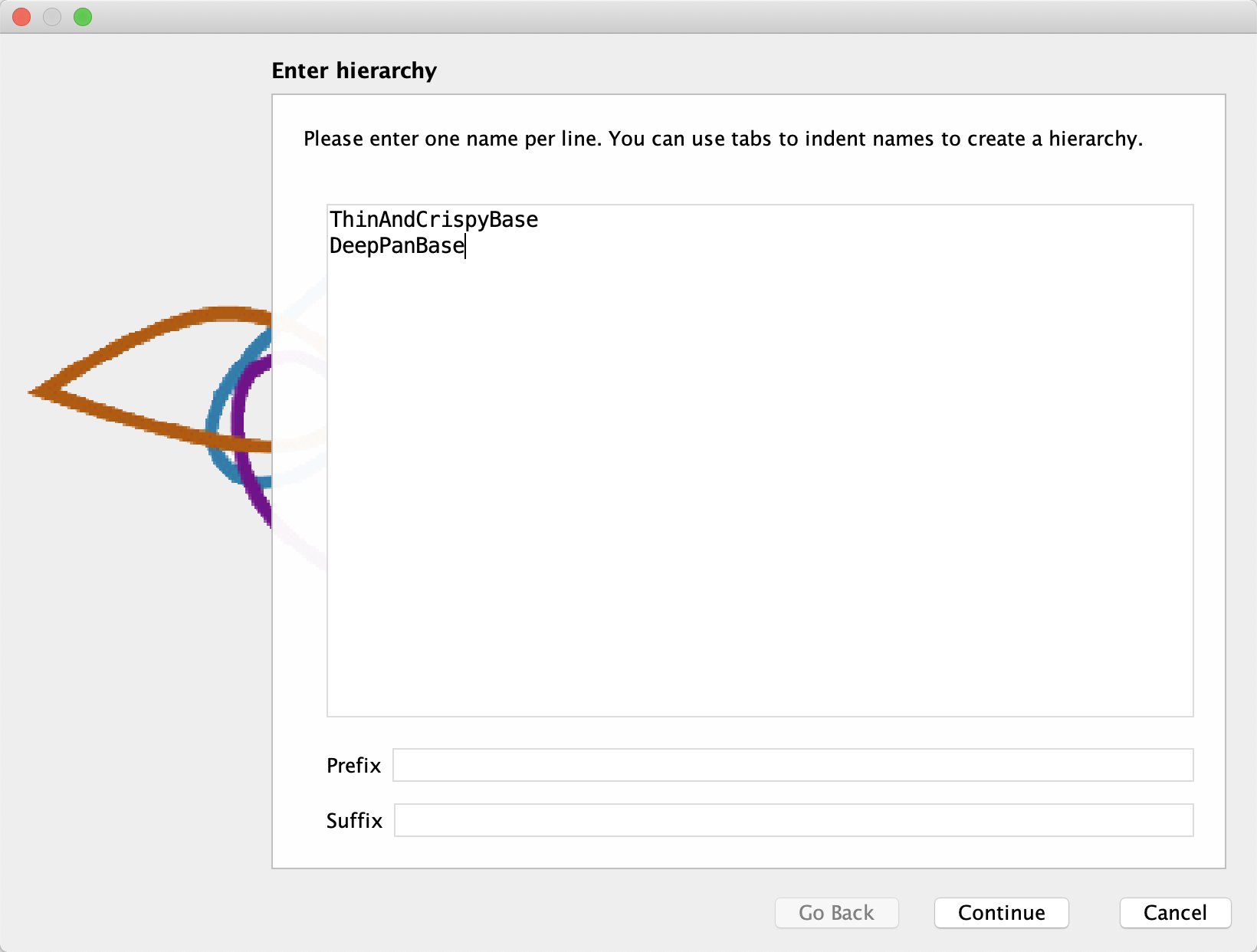
使用 Create Class Hierarchy 来创建类
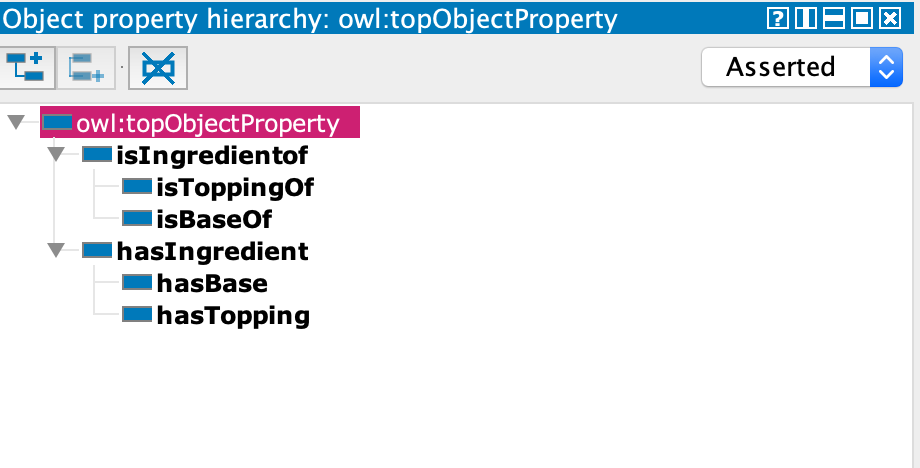
下面介绍一种同时创建多个子类的方法。选中 PizzaBase,点击 Tools -> Create class hierarchy,在弹出窗口中逐一输入类名即可。注意:类名不可重复,可批量添加前缀和后缀,默认类之间 disjoint:
同理,创建 PIzzaTopping 的子类,可以在创建时使用 tab 来进一步划分子类。最终的类层级结构如下:
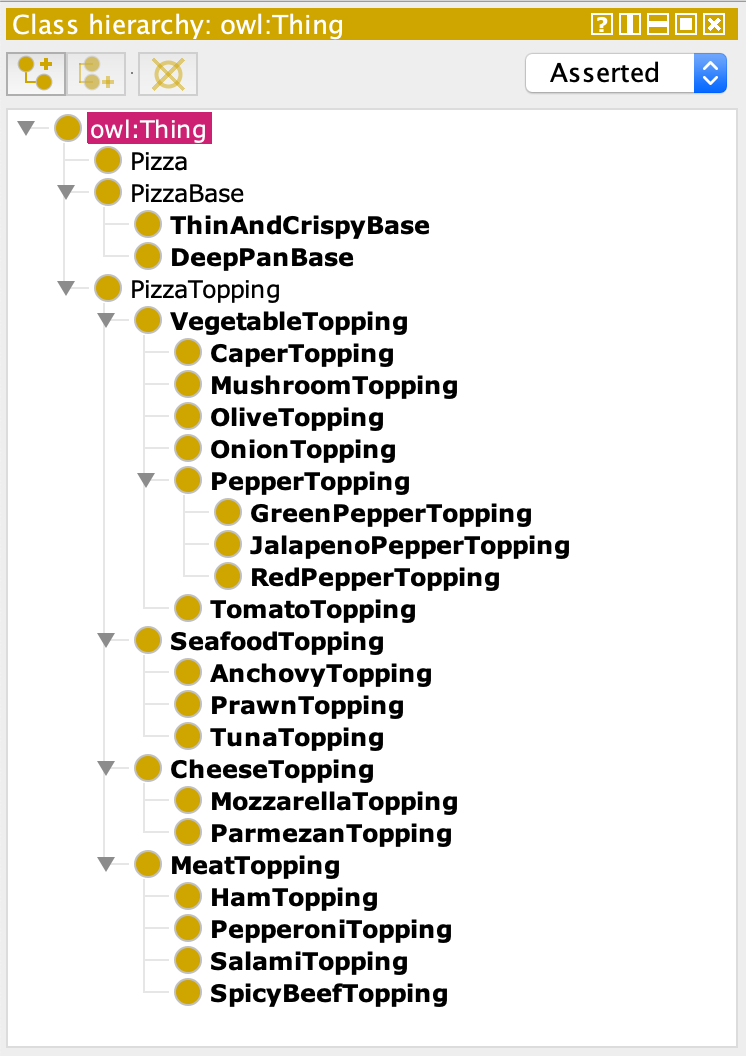
在 OWL 本体中,子类意味着其实例均为父类的实例:
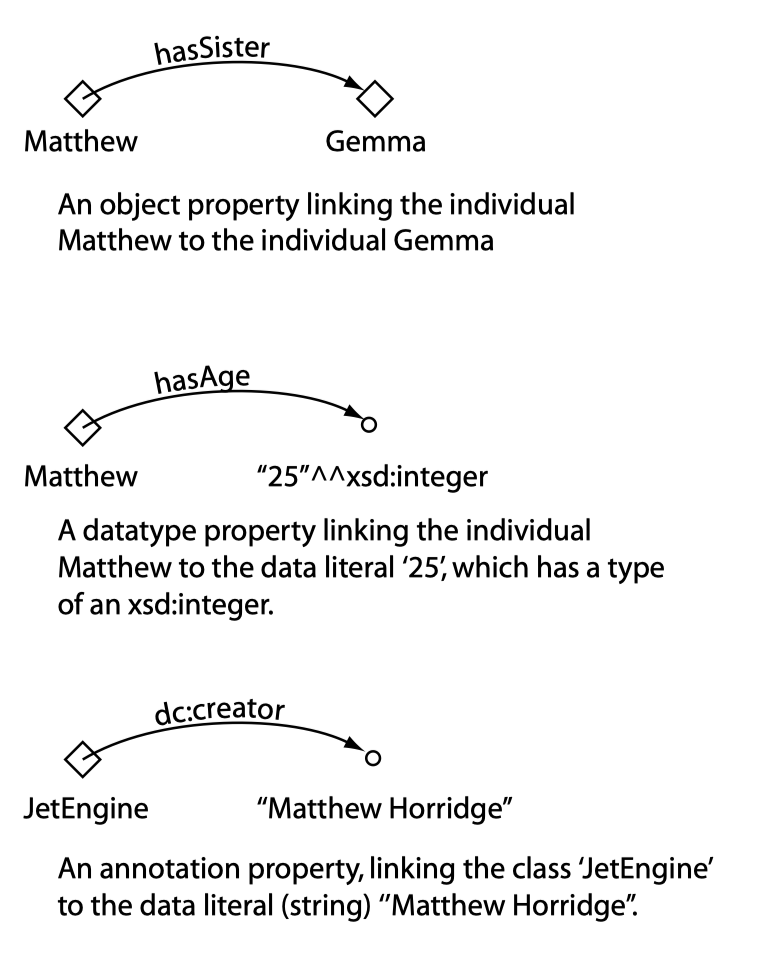
OWL 属性
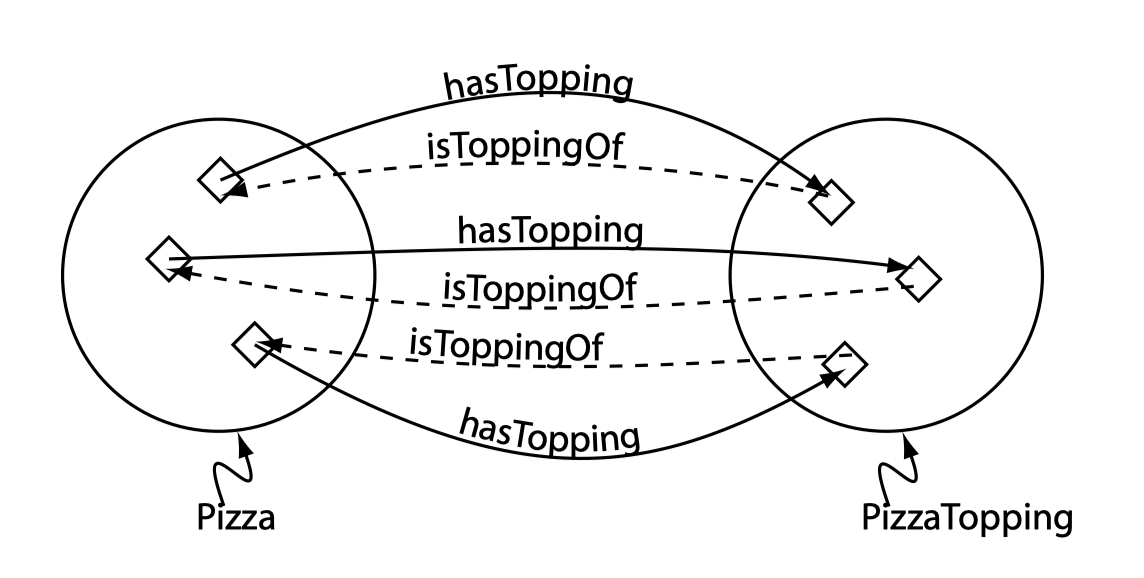
OWL 属性主要分为两种:Object 属性和 Datatype 属性。还有一种属性是 Annotation 属性,用于补充信息。下图给出了各个属性的说明:
在 Object Properties Tab 中(需要手动打开)新建如下属性:

关于属性建议采用小驼峰命名,并使用 has 等前缀提升可读性。属性可以拥有子属性,但要注意属性类型必须相同,如数据属性不能是对象属性的子属性。
转置属性
每个对象属性都可以拥有一个转置属性:
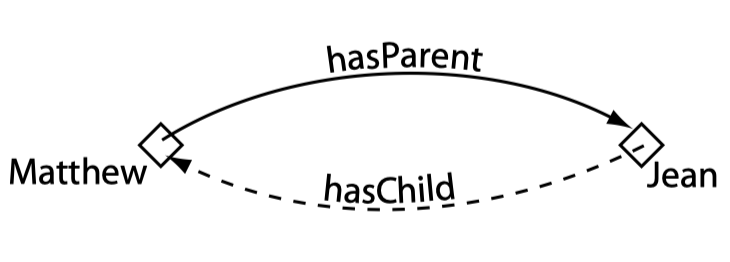
我们可以新建如下转置属性,并通过 Inverse of 将其关联起来:
对象属性特征
OWL 通过属性特征来使得属性的意义更加丰富,可选的特征如下:
功能(Functional)属性
功能属性的对应个体至多为一个,有时也被称为单值属性。如果一个个体通过功能属性连接两个名称不同的个体,则那两个个体必须声明为同一个,否则系统会推理出矛盾。
转置功能(Inverse functional)属性
转置功能属性指该属性的转置属性为功能属性。
传递(Transitive)属性
传递属性可以将属性关系在个体间传递,一个传递属性的转置属性也是传递属性。传递属性不能是功能属性
对称(Symmetric)属性
对称属性的本身即为其转置属性。
非对称(Asymmetric)属性
即其转置不为自己的属性。
反身(Reflexive)属性
反身属性一定要关联个体自身,也可以关联其他个体。
非反身(Irreflexive)属性
非反身属性即属性不能关联个体自身。
实践
设置 hasIngredient 及其转置属性为传递属性。

同理,设置 hasBase 为功能属性,其转置为转置功能属性。
属性的域和范围
属性可以指定域和范围,将来自域的个体连接到来自范围的个体。
- 域是指属性左侧的个体所属的类
- 范围是指属性右侧的个体所属的类
属性的域或范围可以有多个类,取其交集。一般来说,一个属性的域是其转置属性的范围,反之亦然。
需要注意的是,域和范围并不是一个限制,而是会作为推理的公理,比如设置一个 IceCream 个体的 hasTopping 属性,并不会报错,而是会将其推理为 Pizza 的子类。因此,实际上并不建议设置域和范围,容易在比较大的本体中引起 bug。
实践:设置 hasTopping 和 hasBase 属性的域和范围(及其转置属性)
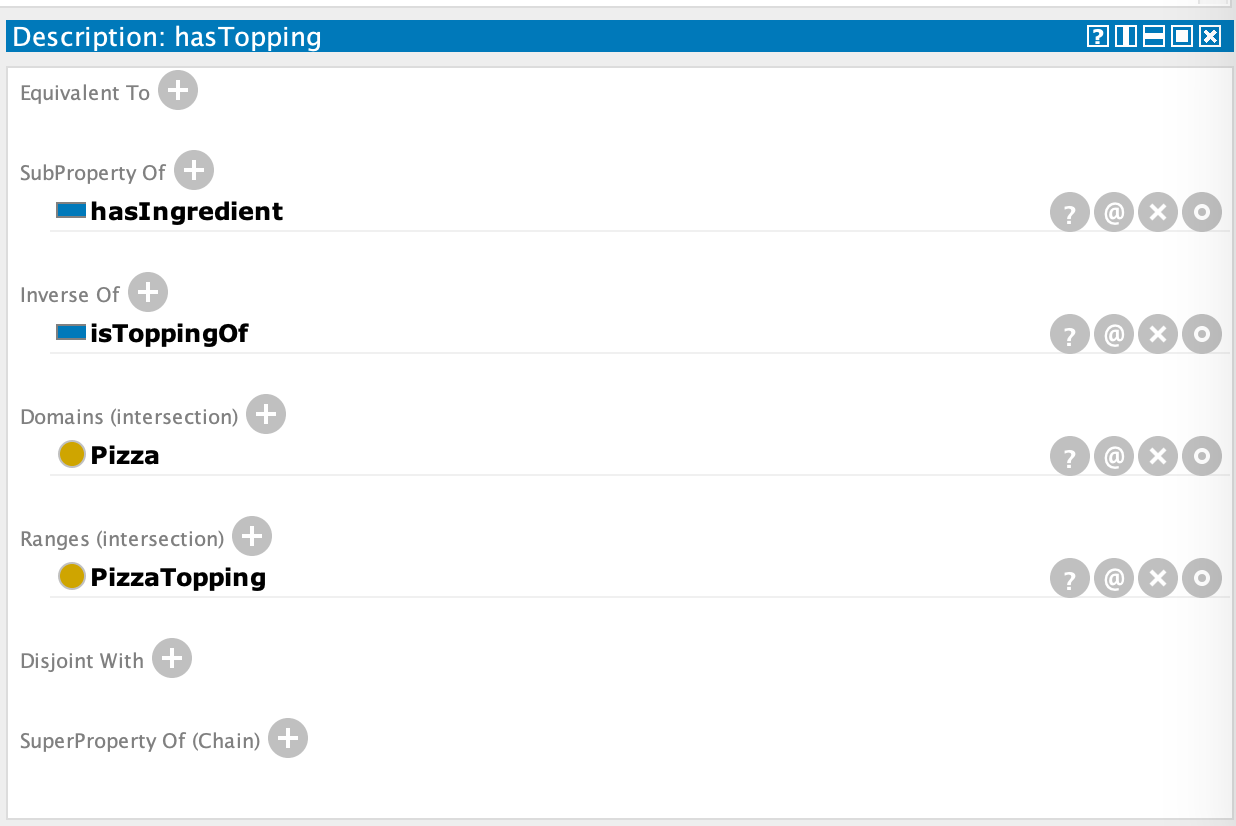
描述和定义类
创建了这么多属性后,现在我们将使用这些属性来描述与定义类。我们可以将所有含有相同属性的个体归到一个匿名类中,这种匿名类称为限制(Restrictions)。
OWL 的限制分为三类:量词(Quantifier)限制、基数(Cardinality)限制和个体(hasValue)限制。本节我们将介绍 Quantifier 限制,其又可以分为两类:
- 存在性(Existential)限制:描述类中的个体至少包含一个指定的属性,连接至指定的类中的个体,其使用 some 关键字
- 普遍性(Universal)限制:描述类中的个体的特定的属性只连接至指定的类中的个体,其使用 only 关键字
存在性限制是最常用的一种限制,可以将其理解为一种必要性。例如,要想成为一个 pizza,其需要有一个(至少一个)pizza 基底:
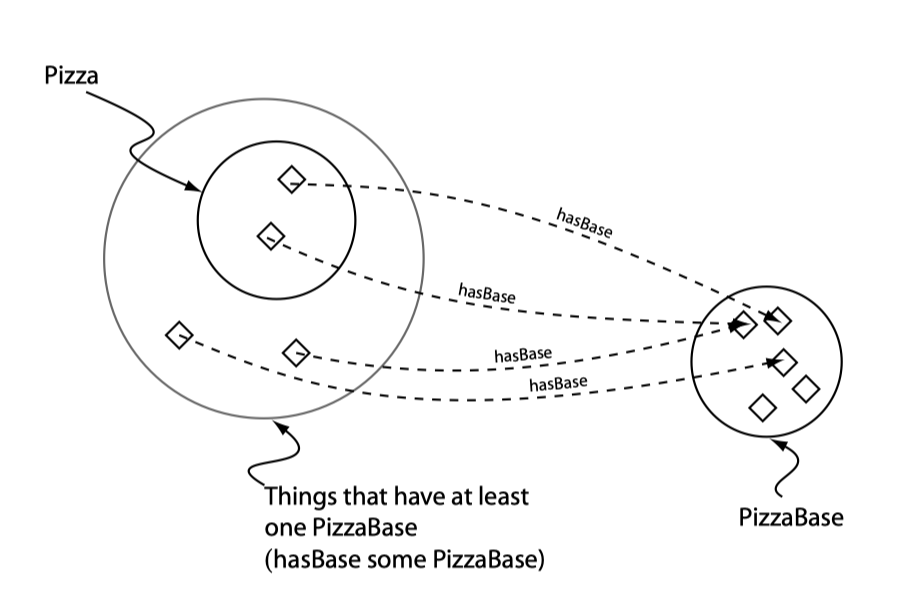
下面我们使用 Class 中的 subclass of 来创建一些不同种类的 pizza,并为其设置存在性限制,注意右键设置 make primitive siblings disjoint:

使用推理机
使用 OWL-DL 描述的本体的一大特点是其可以通过推理机进行处理。推理机的功能主要有两个:
- 推理类的层级结构(一个类是否为另一个类的子类)
- 测试一个类的稳定性(是否可能存在实例)
在 protege 中的菜单中选择推理机,执行推理。可选的推理机有很多,这里选择 pellet。推理机会给出推理的层级结构,并标红不稳定的类:
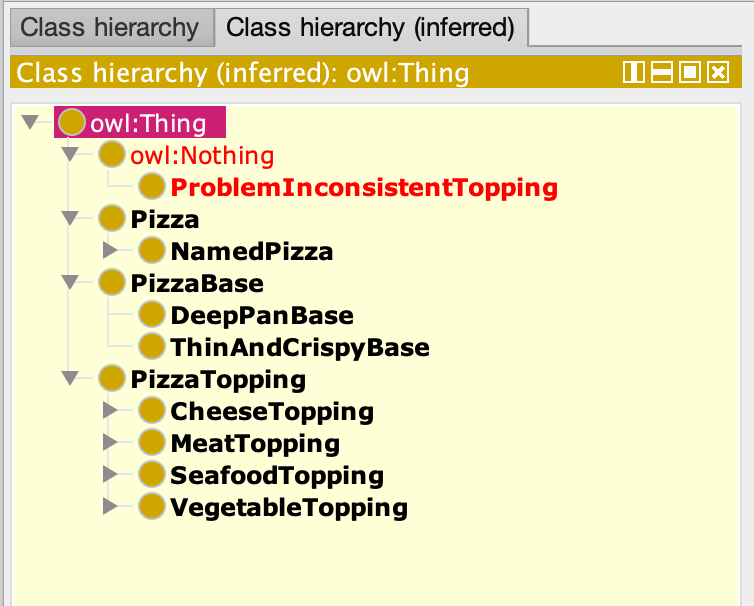
上面的类不稳定的原因是其同时属于两个不相交的父类,因此对于兄弟类,正确地设置其相关性十分重要。
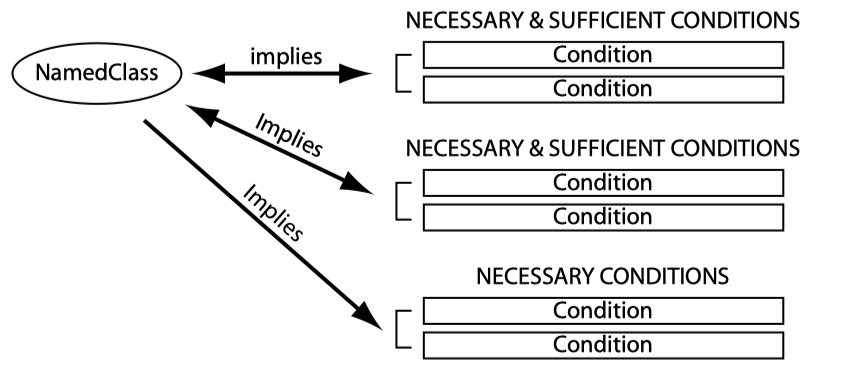
充要条件(原始类与定义类)
到目前为止,我们只使用了必要条件来描述类,只包含必要条件的类称为原始类(Primitive Class)。我们可以添加充要条件来定义类。
包含至少一个充要条件的类称为定义类(Defined Class)
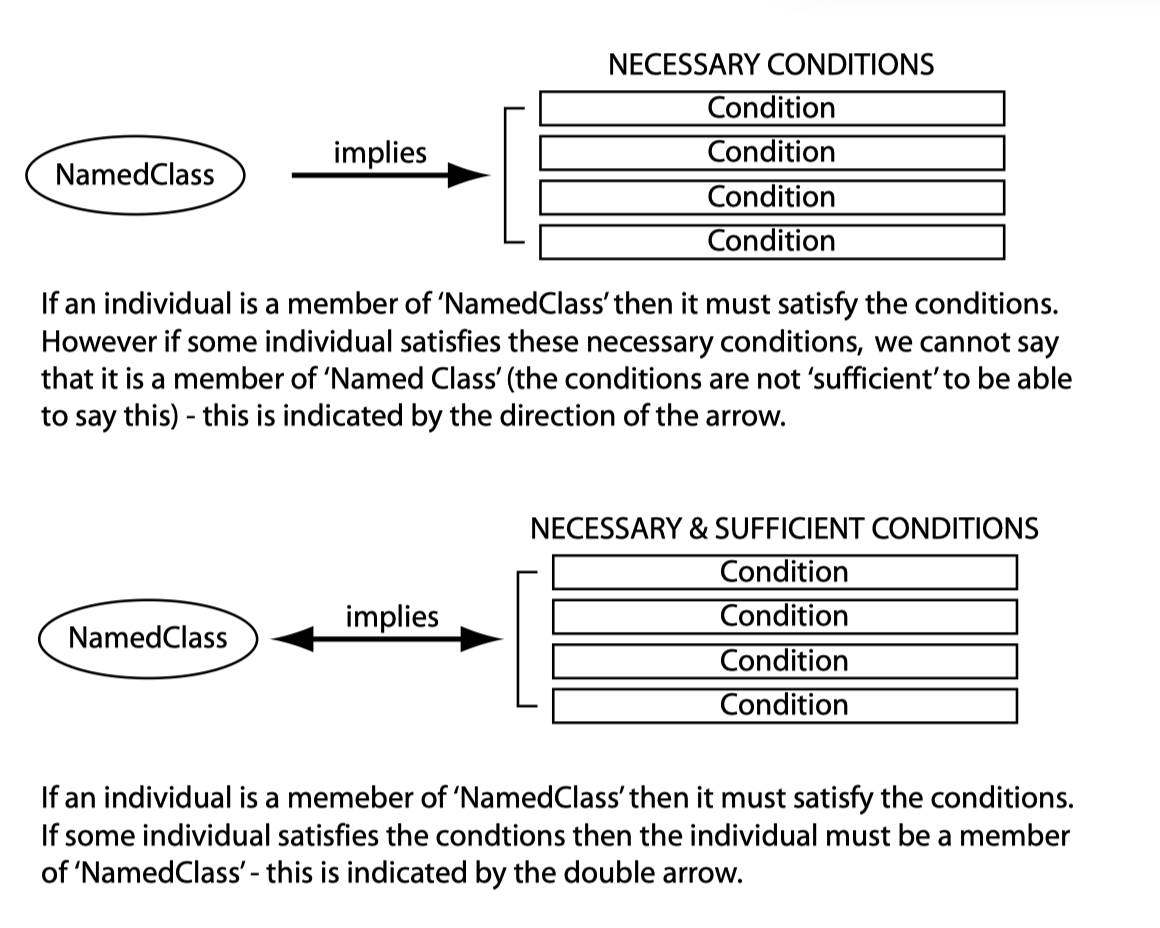
在 protege 中,右键可以自动将原始类转换为定义类(也可以自己设置充要条件):

充要条件的主要作用是帮助推理机推理类的层级结构,推理机只会自动推理定义类下的类。
自动化分类
在较复杂的本体中,使用推理机来推理类的层级结构十分重要。
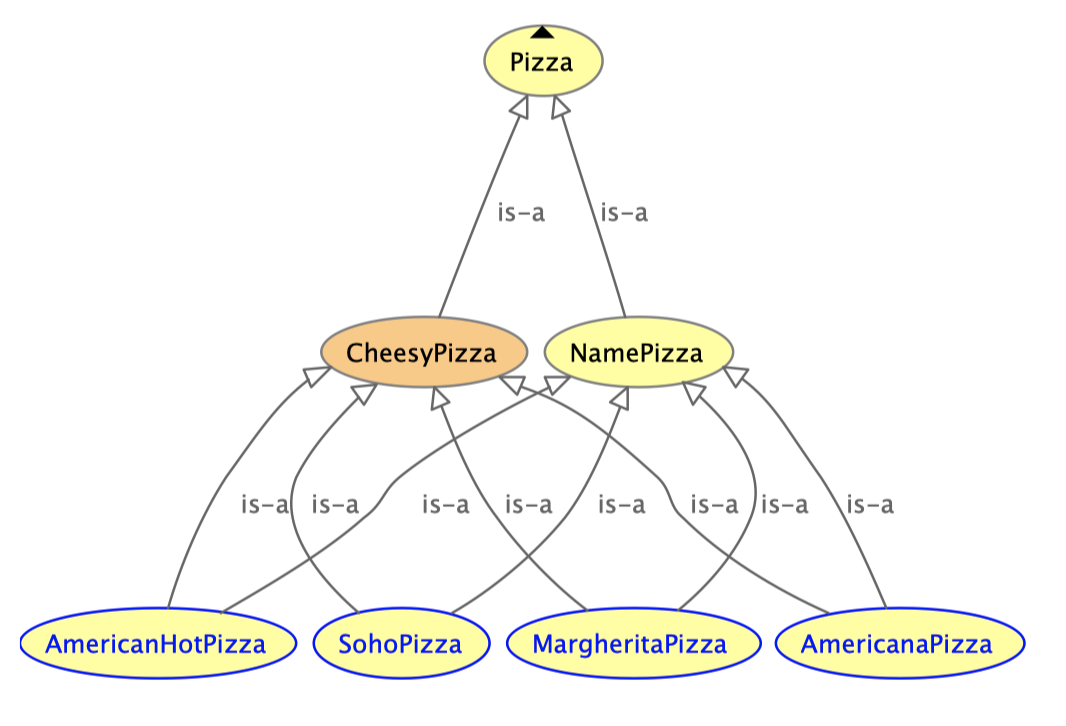
通常手工构建的层级结构(asserted hierarchy)建议以简单树结构组织,即每个子类只有一个父类。这样做便于维护且不易出错。复杂树结构由推理机自动推理完成,下面给出一个例子(注意不能设置 NamedPizza 与 CheesyPizza 的 disjoint):
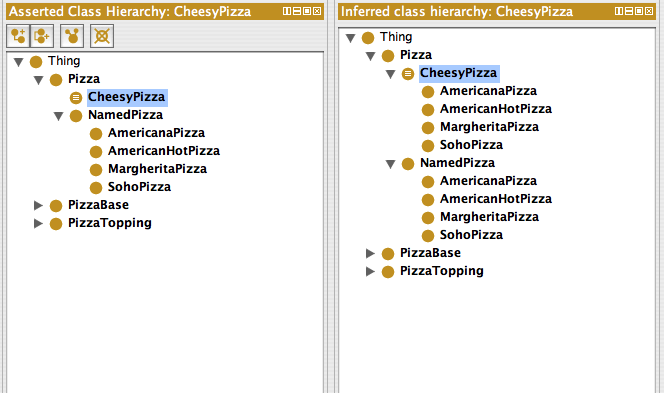
由 OWLViz 给出的层状结构如下:
asserted hierarchy:
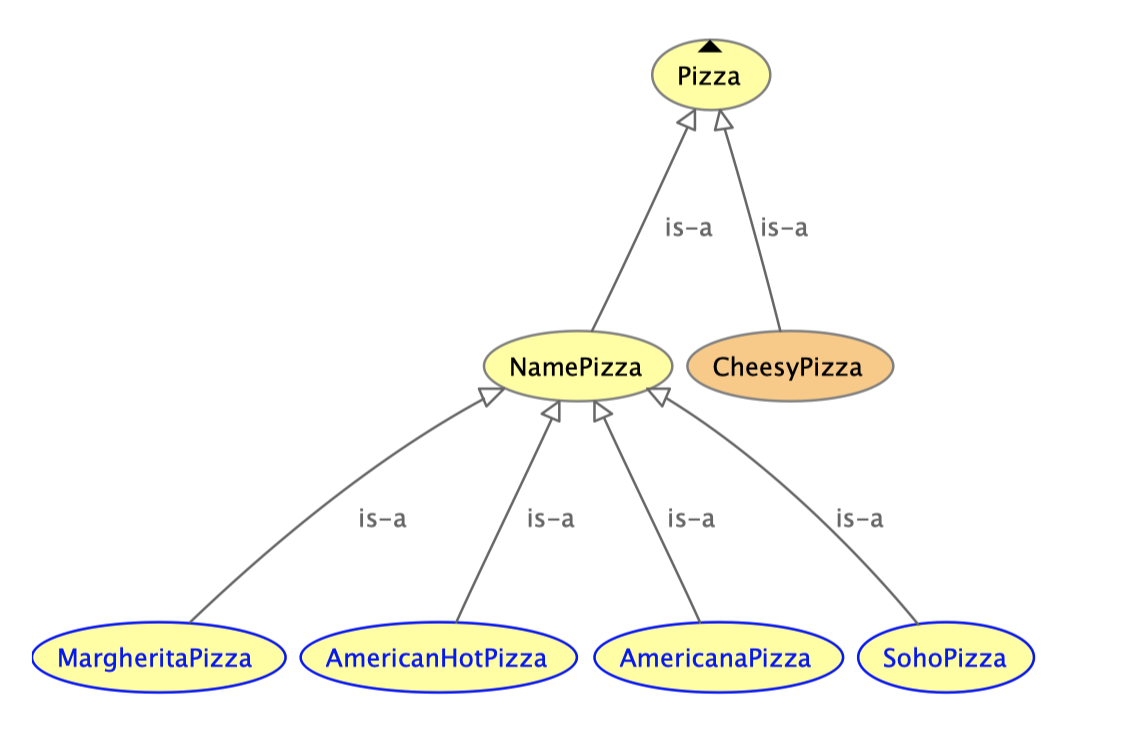
inferred hierarchy:
普遍性限制
之前我们所说的都是存在性限制,其描述类中的个体至少包含一个指定的属性,连接至指定的类中的个体。
现在我们将介绍普遍性限制,其表示类中的个体对于给定属性,只能连接至指定的类中的个体,不能为其他,因此也被称为 AllValuesFrom 限制。
需要注意的是,如果一个个体没有给定的属性,它也满足普遍性限制。普遍性限制给出的是一种 if 关系:如果存在给定属性,则其必须指向指定的类。
下面我们来创建一个 VegetarianPizza 类,并添加普遍性限制。注意要使用 or 而不是 and,否则该条件是无法满足的(因为两个 Topping disjoint)。该限制表示此类如果有 Topping,只能是 Cheese 或 Vegetable,如果此类没有 Topping,也满足条件:

上述条件是必要条件,下面将其转化为充要条件:

自动化分类与开放世界推理
根据上面的定义,似乎 MargheritaPizza 和 SohoPizza 都应该属于 VegetarianPizza。但实际上推理机并不会给出上述推理。这是因为推理机的推理是基于开放世界假设的:
如果一个东西没有被声明是真的,它并不能假定为假。
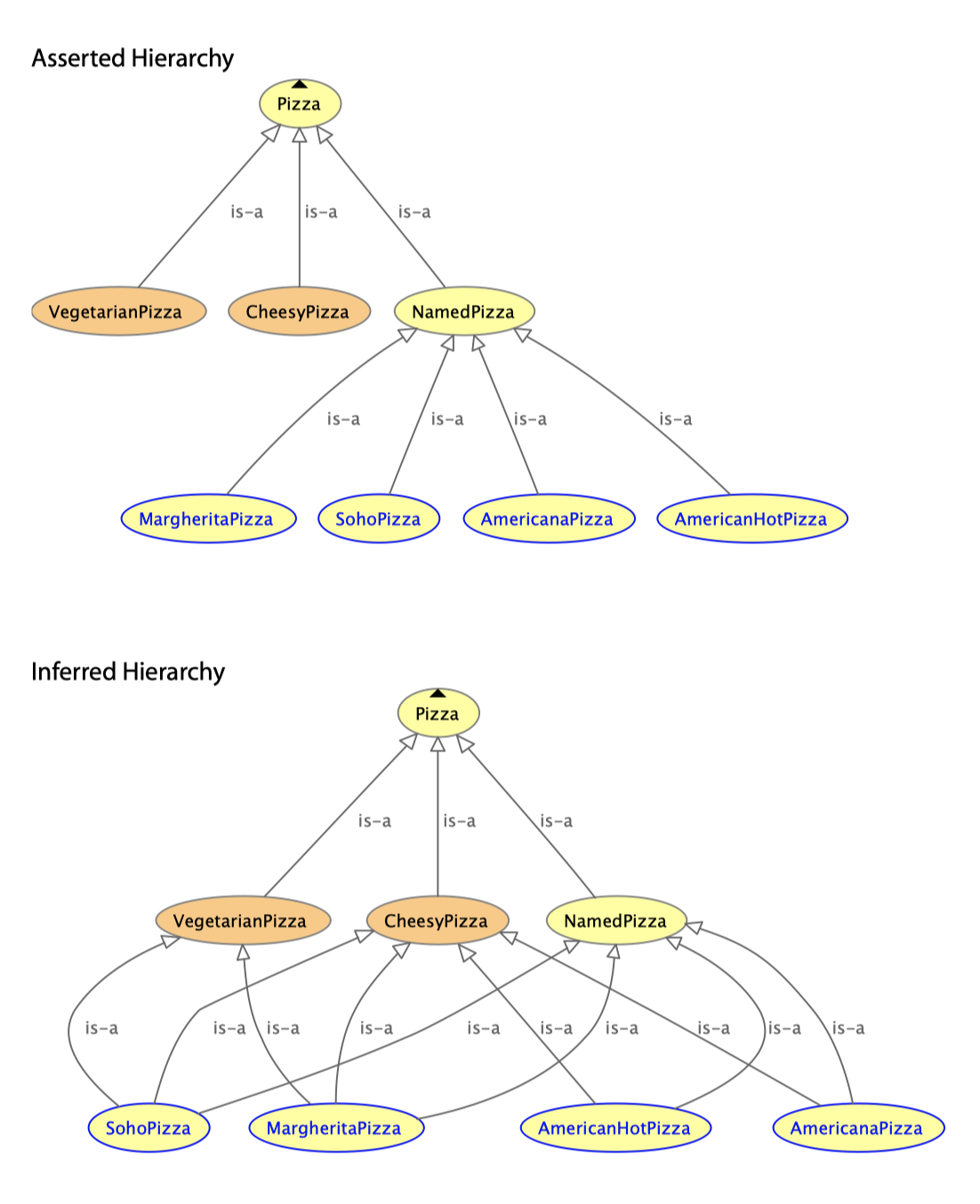
即该知识只是没有添加进知识库,并不代表其不存在。在上面的例子中,我们并不能保证 MargheritaPizza 和 SohoPizza 没有其他的 Topping。因此我们需要对 hasTopping 属性设置一个闭包公理(closure axiom)。
一个闭包公理就是对指定属性的一个普遍性限制,可以在存在性限制上右键自动添加。注意:单独的普遍性限制并不足够,因为可能包含没有 Topping 的 Pizza,虽然从实际生活的角度来说不合理,但是在推理上没有问题。

断言本体(手工创建)和推理本体如下图所示:
值分割
本章节我们将介绍值分割(Value Partitions),它并不是 OWL 的特性,而是一种本体构建中的设计模式。
值分割用于补充我们对类的描述,下面给出在 OWL 中创建一个值分割的例子:
- 创建一个类 SpicinessValuePartition
- 创建其子类表示可能的选项:Hot、Medium 和 Mild
- 使各子类 disjoint
- 设置一个 covering 公理(实际操作为设置一个 Equivalent classes)
- 创建一个功能性对象属性 hasSpiciness
- 将该属性的范围设置为 SpicinessValuePartition
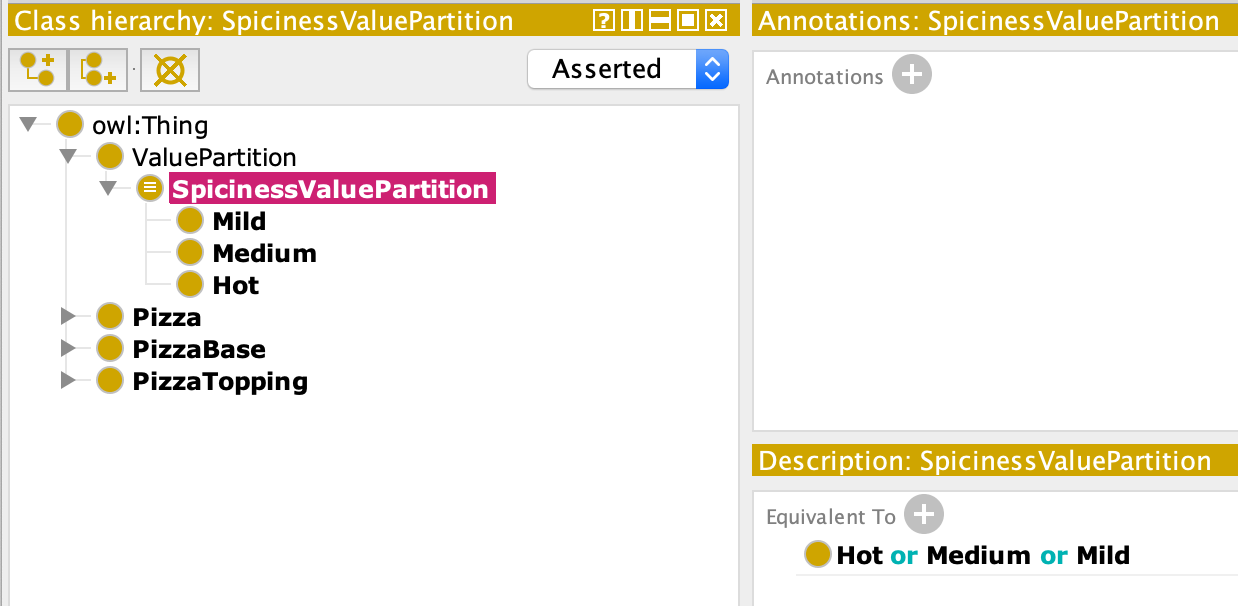
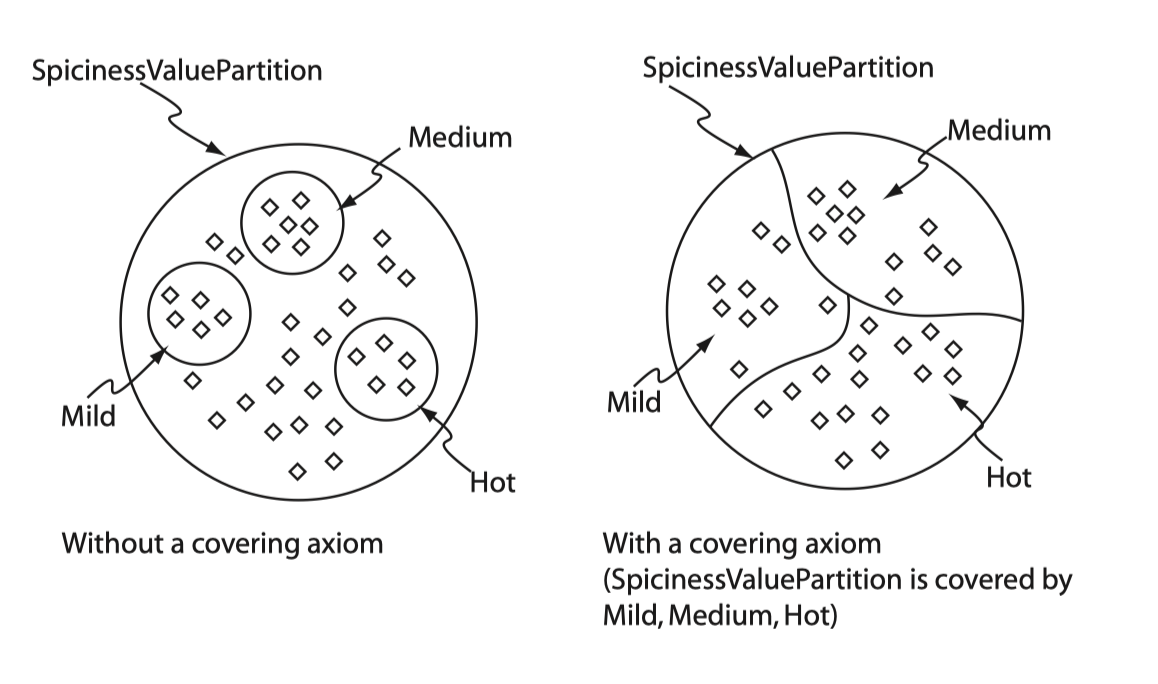
covering 公理的作用是表明该类的全部组成成分,下图给出了很好的说明:
下面基于上述属性添加存在性限制给每个具体的 Topping 类,可以使用 tab 里的 class matrix 批量添加:

最后,我们创建一个 SpicyPizza 类,并使用嵌套语句进行定义:

基数限制
基数限制用于描述关系(对象属性或数据类型属性)的数量,分为:
- 最少 min
- 最多 max
- 具体数量 exactly
只有关系所指向的个体确定与其他个体不同,才会作为一个关系计数。
下面我们设置一个新的 Pizza 类,定义其 hasTopping 关系至少为三条:

实际上,我们还可以再缩小基数限制的范围,设置 qualified 基数限制,只要在设置基数限制时添加具体的类即可,实际上 unqualified 所指定的填充类是 Thing。
注意:上面的限制只表明该类需要以 hasTopping 关系连接 4 个 CheeseTopping 个体,并不代表不能连接其他 Topping 个体,我们需要通过普遍性限制(only )加以约束:

数据类型属性
之前我们介绍的都是对象属性,下面介绍另一种属性:数据类型属性。
数据类型属性将个体和具体数值连接起来,该数值类型一般为 xml schema datatype 或 rdf literal。我们可以通过 datatype properties tab 创建 datatype 属性。将属性设置为 functional 可以保证每个个体只能有一个该属性:
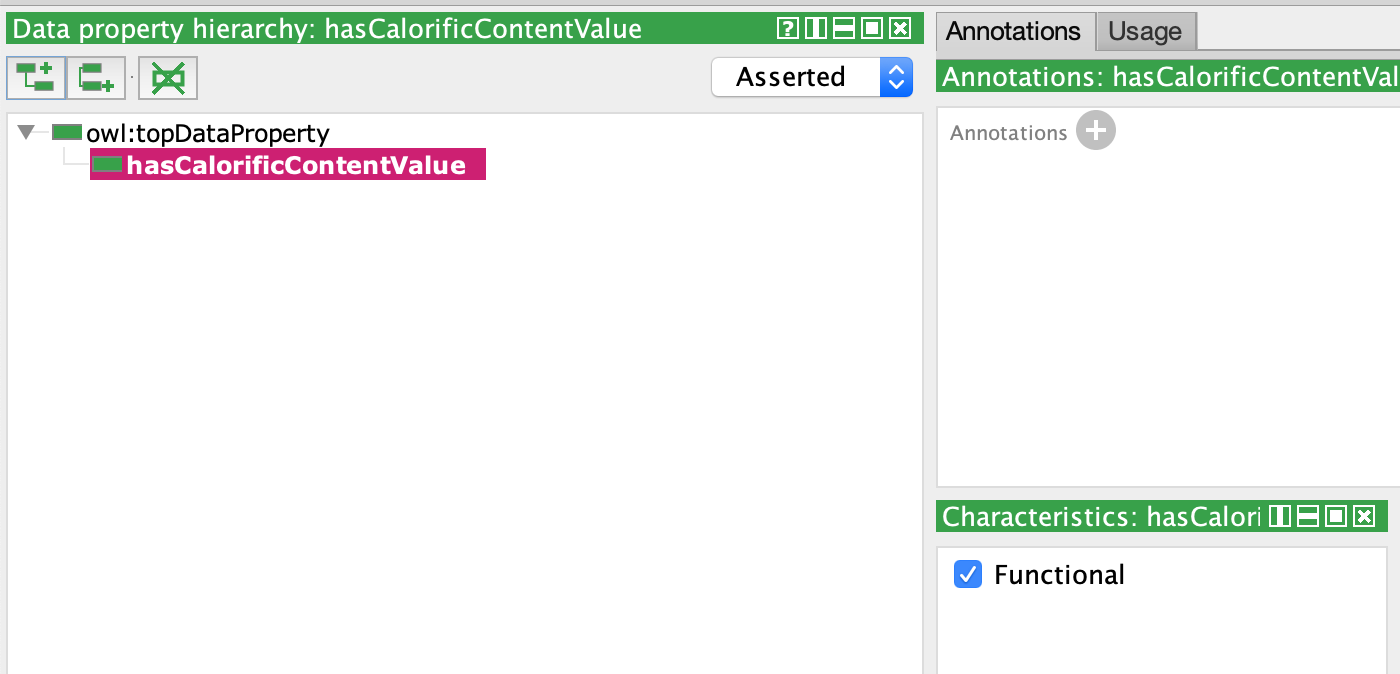
下面我们将创建两个个体,并设置其 hasCalorificContentValue 属性:
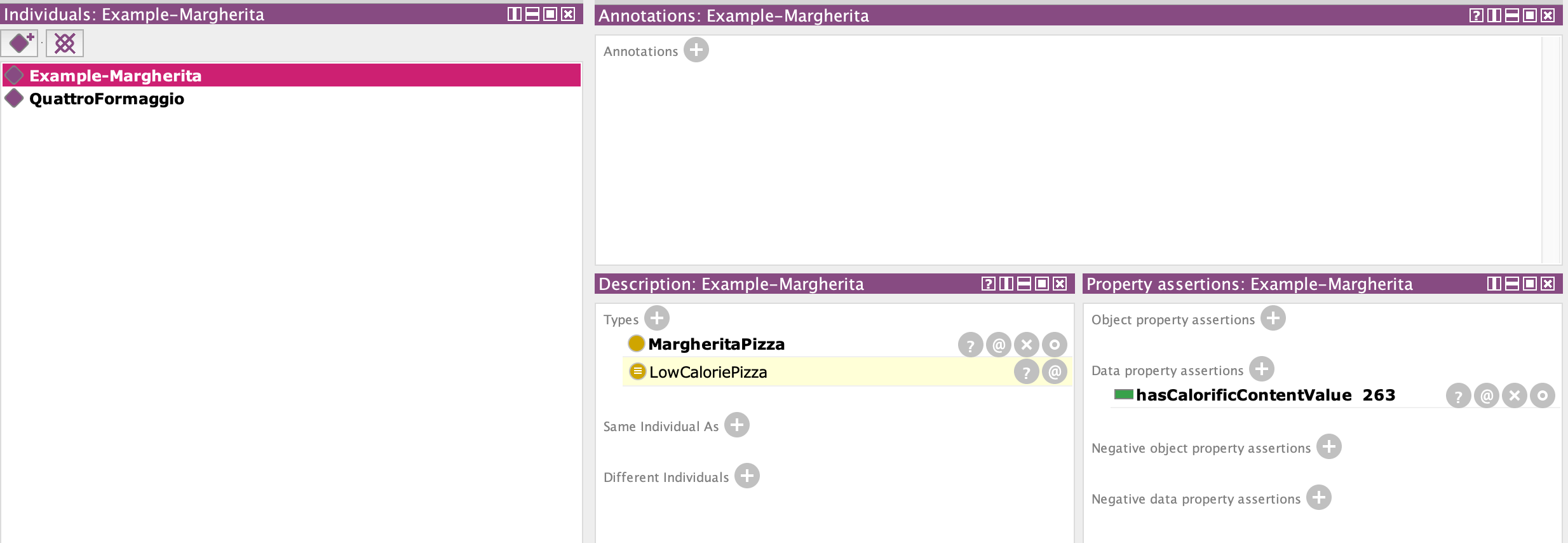
最后,定义两个新的 Pizza 类,并使用数据类型属性对其进行约束,推理机会自动将上面两个个体归到相应的类中:
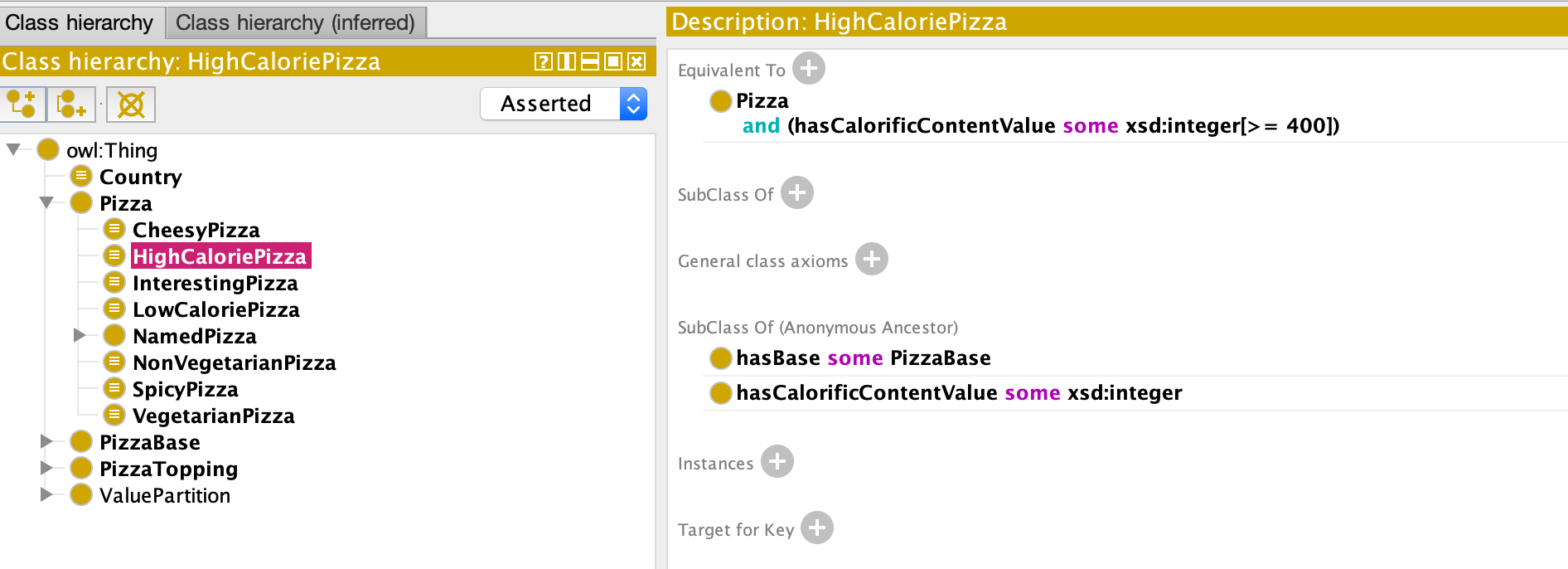
开放世界推理
下面我们将创建一个 VegetarianPizza 类的互补类 NonVegetarianPizza,以此进一步展示开放世界推理。
NonVegetarianPizza 类的定义如下,设置限制时可以使用 tab 自动补全类名:

通过自动推理可以发现,不属于 Vegetarian 的类都被归到了 NonVegetarianPizza 下

然而,如果我们创建一个不含有闭包公理的类,其将不会被归到任何一个类下。这是因为在开放世界假设下,UnclosedPizza 不能确定是否属于 Vegetarian 类,也就不能确定是否属于 NonVegetarianPizza。
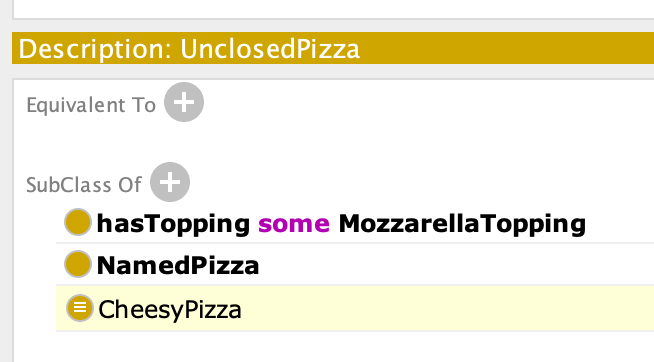
创建其他的 OWL 部件
创建个体
新建一个 Country 类,创建一些个体。因为 OWL 不使用唯一命名假设,所以必要时需要设置个体的独立性。

hasValue 限制
hasValue 限制用于描述个体至少有一个指向特定个体的关系:

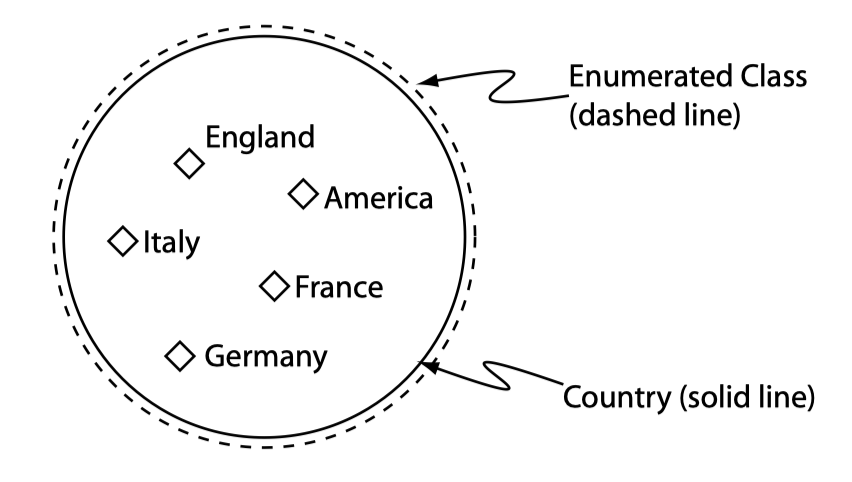
枚举类
枚举类用于表示该类只由一些特定的个体组成。枚举类本质上是一种匿名类,可以将其与命名类通过 equivalent class 关联起来:

下面的图描述了枚举类和命名类的关系:
注释属性
OWL 允许为类、属性、个体和本体本身添加注释属性: - OWL-Full 对注释属性的使用没有限制 - OWL-DL 限制了注释属性的类型和属性公理
多个充要条件
之前介绍的类都只有一个充要条件,实际上我们可以通过 add 添加多个充要条件:
SWRL 语言
SWRL 语言是一种基于 OWL 的规则语言,用于提供更加强大的演绎推理功能。
SWRL 规则样式
SWRL 规则由两部分组成,
- 前半部分称为 body
- 后半部分称为 head
每个部分又由多个原子(atom)连接而成:
atom ^ atom .... -> atom ^ atom .... |
可以理解为如果 body 中的条件均满足,则 head 中的结论为真。SWRL 不支持否定连接。
一个 atom 的形式如下:
p(arg1, arg2, ... argn) |
p 是一个谓词符号,可以表示本体中的各种概念,下一节会介绍。arg 为参数,一般表示个体或数据值的变量,或直接表示某个特定的个体或值。
Atom 类型
SWRL 提供以下七种 atom:
- Class Atoms
- Individual Property atoms
- Data Valued Property atoms
- Different Individuals atoms
- Same Individual atoms
- Built-in atoms
- Data Range atoms
Class Atom
由一个 OWL 命名类(或类表达式)以及表示 OWL 个体的单个参数构成:
Person(?p) |
下面的例子表示所有属于 Man 的个体也属于 Person(这一逻辑其实 OWL 本身也可以实现):
Man(?p) -> Person(?p) |
Individual Property Atom
由一个 OWL 对象属性和两个表示 OWL 个体的参数构成:
hasBrother(?x, ?y) |
下面的规则表示有男性 sibling 的人类可以理解为有一个 brother:
Person(?p) ^ hasSibling(?p, ?s) ^ Man(?s) -> hasBrother(?p,?s) |
Data Valued Property Atom
由一个 OWL 数据类型属性和两个参数组成,第一个参数表示个体,第二个表示数值:
hasAge(?x, ?age) |
下面的规则表示有车的人是驾驶员:
Person(?p) ^ hasCar(?p, true) -> Driver(?p) |
也可以使用具体的个体:
Person(Fred) ^ hasCar(Fred, true) -> Driver(Fred) |
Different Individuals Atom
由 differentFrom 符号和两个表示 OWL 个体的参数组成:
differentFrom(?x, ?y) |
Same Individual Atom
由 sameAs 符号和两个表示 OWL 个体的参数组成:
sameAs(?x, ?y) |
Data Range Atom
由一个数据类型名(或字面量集合)和一个表示数据值的参数构成:
xsd:int(?x) |
Built-In Atom
事先定义好的规则,支持用户自定义:
Person(?p) ^ hasAge(?p, ?age) ^ swrlb:greaterThan(?age, 17) -> Adult(?p) |
一般只支持数据类型属性,不过 SWRLAPI 支持用户自定义对个体、类和对象属性的扩展,自定义 atom 的合法性需要由定义者指定。
常见问题
问:内置 atom 能否绑定参数?
答:可以,只要该变量没有被事先绑定值。
Rectangle(?r) ^ hasWidthInMeters(?r, ?w) ^ hasHeightInMeters(?r, ?h) ^ |
问:类表达式可以用于 SWRL 规则吗?
答:可以
(hasChild >= 1)(?x) -> Parent(?x) |
问:SWRL 遵循开放世界假设吗?
答:是的,具体体现在两点:
- 不同名称的个体可能相同,需要进行判断:
Publication(?p) ^ hasAuthor(?p, ?y) ^ hasAuthor(?p, ?z) ^ differentFrom(?y, ?z) |
- 无法明确个体或属性的具体数量(因为没有声明不代表不存在)
比如 (hasChild >= 1)(?x) -> Parent(?x) 这条规则,可能会匹配没有明确 hasChild 属性的个体,需要在本体中额外添加约束。
问:SWRL 是否支持非单调的推理?
答:不支持,即不能修改本体中已有的信息(否则会报错)
问:SWRL 支持否定吗?
答:SWRL 不支持否定式,但是支持类的否定表达式:
(not Person)(?x) -> NonHuman(?x) |
注意:由于开放世界假设,只有明确与 Person disjoint 的类才会应用规则。
问:SWRL 支持 atom 的分离吗?(即或表达式)
答:不支持,可能引起歧义,可以通过拆分表达式来解决。但是 SWRL 支持联合类表达式:
(A or B)(?x) -> C(?x) |
问:SWRL 是否支持 OWL Full?
答:原生不支持,不过 SWRLAPI 提供了对 OWL Full 的有限支持,但建议仅用于本体查询,不要用于推断新知识。
问:SWRL 是否支持 RDF 或 RDFS?
答:不支持,可以先将其转换为 OWL。
问:SWRL 的语法特点?
答:SWRL 提升了表达性,但牺牲了可判定性,即本体推理终止时,SWRL 的推理可能没有终止。SWRL 会采用 DL-Safe 语法来提升可判定性,即只绑定已知的个体,以下面的规则为例:
Vehicle(?v) ^ Motor(?m) ^ hasMotor(?v, ?m) -> MotorizedVehicle(?v) |
如果我们新建了一个 Vehicle 的子类 Car,并为其添加存在性限制 has some Motor,再新建一个该类的个体。上述规则并不会将该个体归类到 MotorizedVehicle,除非它真的包含一个 Motor 个体,而非仅仅是存在性限制。
此外,如果内置 atom 绑定参数,可能会出现不可判定的情况:
Driver(?d) ^ hasAge(?d, ?age) ^ swrlb:add(?newage, ?age, 1) |
上面的规则由于单调性,会产生一系列的 age(非 functional 的情况下),每次产生新的值都会触发规则,导致产生一个无穷大的数。
PS:经测试如果右半部分赋予常数值,该规则会产生一个新的 age 值(不会无限循环),因为同样的属性值只会生成一个,属性为 functional 情况下会报错。
问:能否使用注释值来指向 OWL 实体?
答:可以,但要注意不能重复:
'a Driver'(?d) ^ hasAge(?d, ?age) ... |
问:如何调试 SWRL 规则?
答:可以使用 SQWRL 调试:
Person(?p) ^ hasAge(?p, ?age) ^ swrlb:greaterThan(?age, 17) -> Adult(?p) |
问:应该什么时候使用 SWRL?
答:SWRL 基于 OWL-DL,可以提升本体的表达性,但是以可判定性为代价。如果可能的话,应该尽量使用 OWL ,只在需要额外的表达能力时使用 SWRL。
PS:注意数据属性的推理可能需要手动打开:

附录 A:限制类型
本附录将进一步介绍 OWL 中的属性限制类型,所有类型的限制实际上都是在描述一个包含某些个体的匿名类。当我们在为一个命名类设置限制时,我们实际上是在描述该类的匿名超类:

Quantifier 限制
量词限制包含三个部分:
- 一个量词:存在性量词或普遍性量词
- 一个属性:量词作用的对象
- 一个填充器:属性作用的类
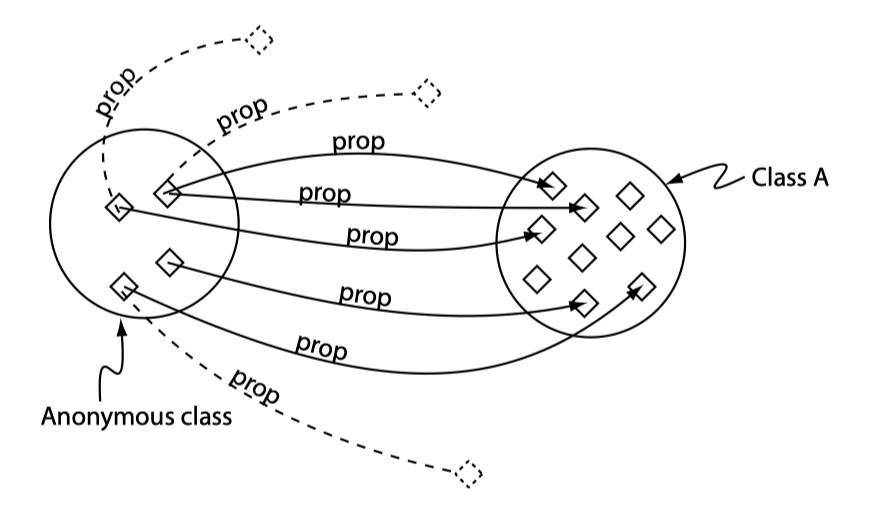
存在性限制与普遍性限制之前已经介绍,这里不作赘述。存在性限制表明至少有一个当前关系对应到指定的类(可能还有其他):
普遍性限制表明当前关系只对应到指定的类(也可能一个没有):

一般将两者结合使用,构造闭包公理。
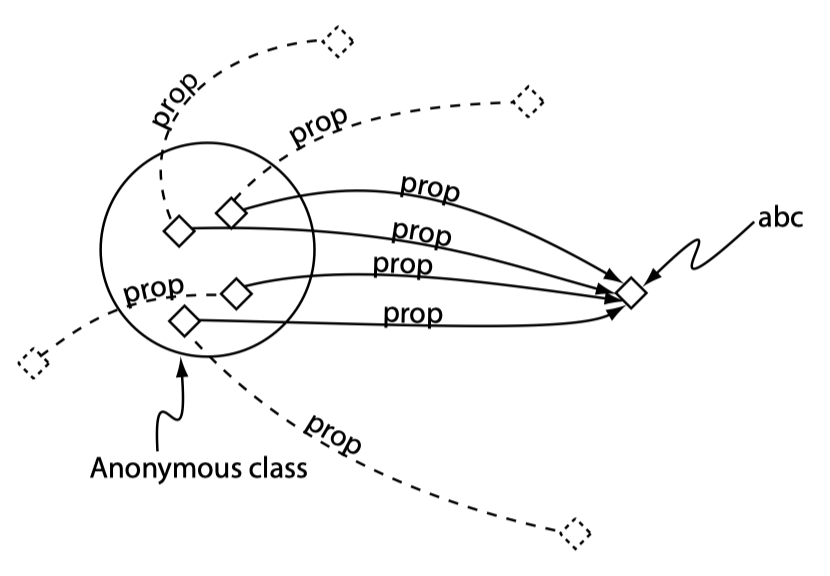
hasValue 限制
hasValue 限制将属性连接至特定的个体,而非特定的类。其等价于存在性限制,其指向的类为包含特定个体的枚举类。
Cardinality 限制
基数限制用于规定个体参与指定属性的关系的数量,可以分为: - 最大 - 最小 - 准确值:可以理解为最大与最小结合的语法糖
由于 OWL 不使用独立命名假设,所以在计算关系数量时,只有明确不同的个体才会计数。如果一个个体对应的基数限制为 2,但该关系对应 3 个个体,则其中两个会被认为是相同的个体。
附录 B:复杂类描述
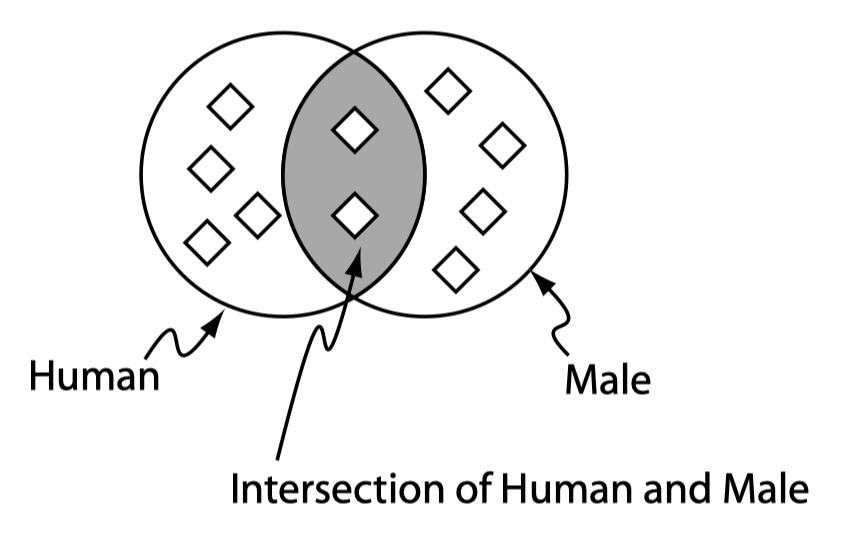
除了用命名类和限制组成的匿名类来定义父类外,我们还可以使用复杂类描述定义的匿名类。复杂类描述分为两种:
AND:构成交叉类
OR:构成联合类
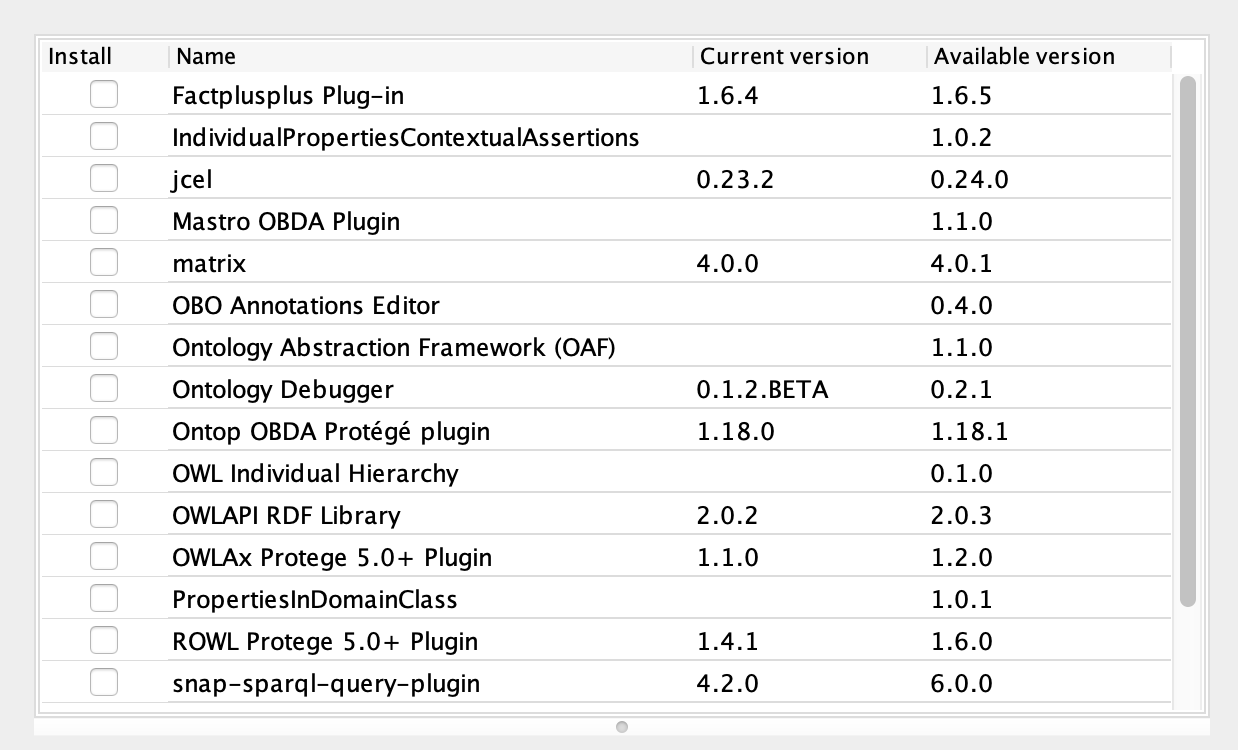
附录 C:插件
Protege 支持许多有用的插件,5.5.0 版本下可通过 File -> Check for Plugins 安装和升级插件:
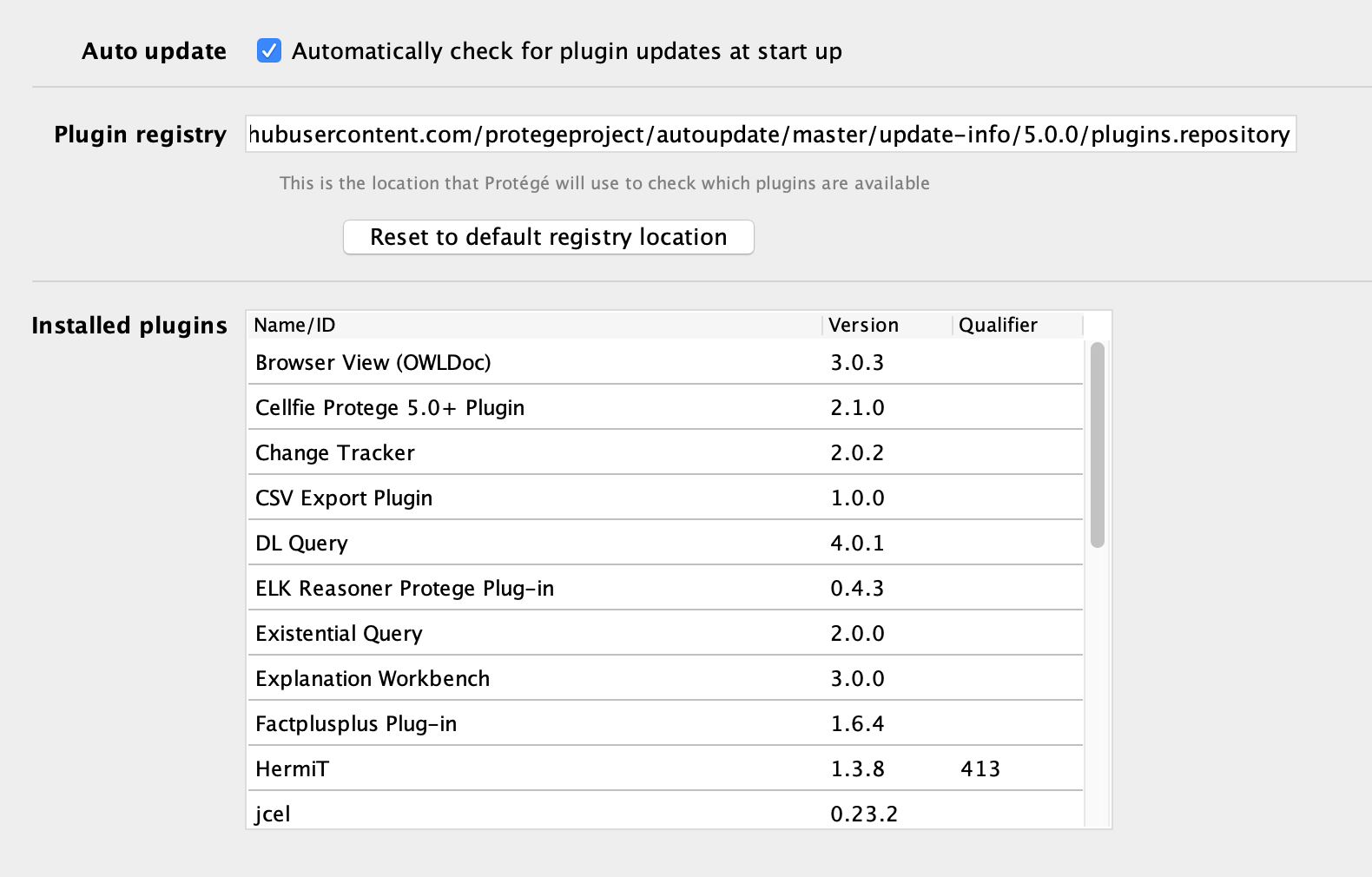
通过 Preference -> Plugins Tab 设置自动检查:
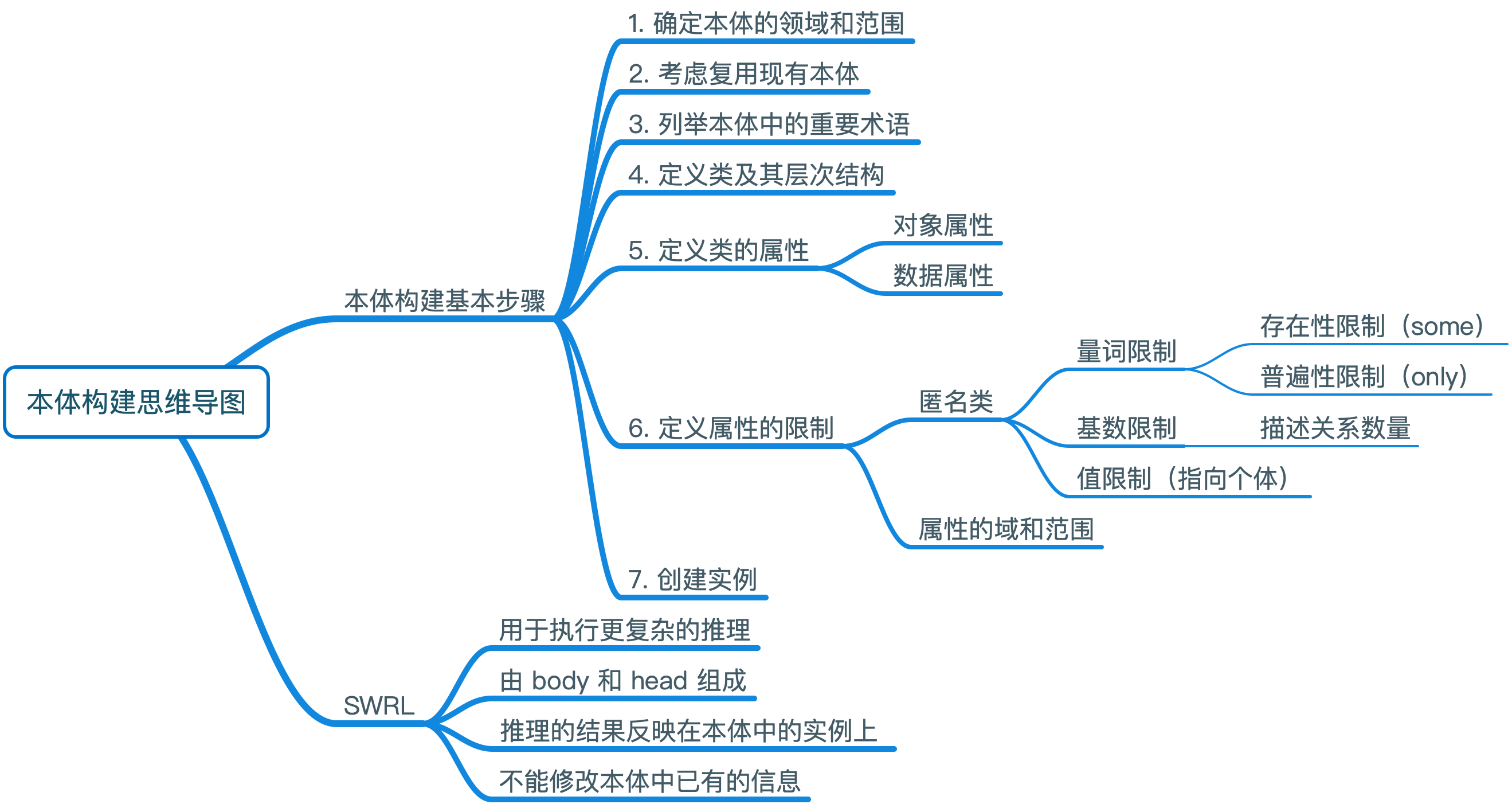
思维导图
PS:点击可下载文中使用的 pizza.owl