LDA 原理第一部分:LDA 数学八卦
本篇博客为对 LDA 的原理解读第一篇,主要参考网上流传已久的文章《LDA 数学八卦》。
Gamma 函数
作者首先介绍了 Gamma 函数: \[ \Gamma(x)=\int_{0}^{\infty} t^{x-1} e^{-t} d t \] Gamma 函数在数学上应用广泛,它可以将阶乘延拓到实数集上: \[ \Gamma(n)=(n-1) ! \] 在概率统计中,Gamma 函数也频繁出现。首先,由 Gamma 函数可以推导出 Gamma 分布: \[ \operatorname{Gamma}(x | \alpha)=\frac{x^{\alpha-1} e^{-x}}{\Gamma(\alpha)} \] Gamma 分布和 Poisson 分布有着密切的联系: + 参数为 \(\lambda\) 的 Poisson 分布,概率写为: \[ \text {Poisson }(X=k | \lambda)=\frac{\lambda^{k} e^{-\lambda}}{k !} \]
- 而 Gamma 分布中取 \(\alpha = k+1\) 得到: \[ \operatorname{Gamma}(x | \alpha=k+1)=\frac{x^{k} e^{-x}}{\Gamma(k+1)}=\frac{x^{k} e^{-x}}{k !} \]
这两个分布在数学形式上是一致的,可以直观地认为 Gamma 分布是 Poisson 分布在正实数集上的连续化版本。
我们可以从二项分布出发,利用其极限是 Poisson 分布的性质,将 Gamma 分布和 Poisson 分布联系起来: \[ \text {Poisson }(X \leq k | \lambda)+\int_{0}^{\lambda} \frac{x^{k} e^{-x}}{k !} d x=1 \] 可以看到,两者的概率累积函数有互补的关系。
Beta/Dirichlet 分布
原文中作者通过一个游戏介绍了各种分布,这里省略过程直接给出重要的结论:
Beta 分布的概率函数为: \[ f(x)=\frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha) \Gamma(\beta)} x^{\alpha-1}(1-x)^{\beta-1} \] 其中 \(\alpha=k, \beta=n-k+1\)
Beta 分布是一种定义区间为 [0,1] 上的连续概率分布,其概率密度图像(某一点的值没有意义)计算如下:
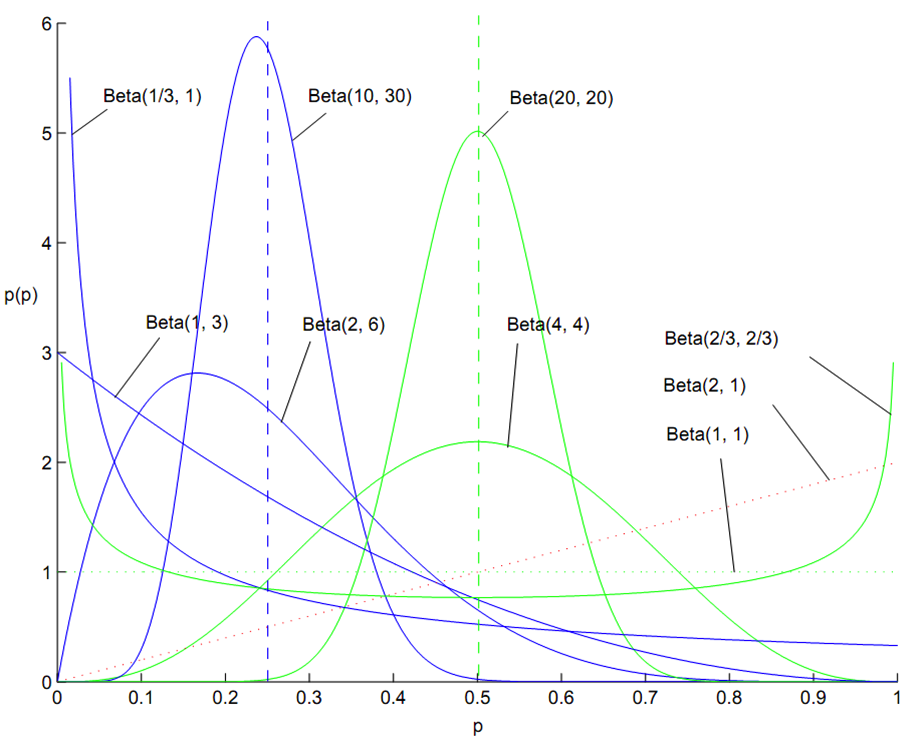
在贝叶斯分析的过程下,可以证明 Beta 分布和二项分布共轭: \[ \operatorname{Beta}(p | \alpha, \beta)+\text {Binom}\left(m_{1}, m_{2}\right)=\operatorname{Beta}\left(p | \alpha+m_{1}, \beta+m_{2}\right) \] 共轭的意思就是:数据符合二项分布的时候,参数的先验分布和后验分布都能保持 Beta 分布的形态,这样便于我们在先验分布中赋予参数很明确的物理意义,这个物理意义可以延续到后验分布中进行解释。
类似地,Dirichlet 分布是 Beta 分布在高维上的推广: \[ \operatorname{Dir}(\vec{p} | \vec{\alpha})=\frac{\Gamma\left(\sum_{k=1}^{K} \alpha_{k}\right)}{\prod_{k=1}^{K} \Gamma\left(\alpha_{k}\right)} \prod_{k=1}^{K} p_{k}^{\alpha_{k}-1} \] 可以证明,Dirichlet 分布与多项分布共轭: \[ \operatorname{Dir}(\vec{p} | \vec{\alpha})+\operatorname{Mult}(\vec{m})=\operatorname{Dir}(\vec{p} | \vec{\alpha}+\vec{m}) \] Beta/ Dirichlet 分布具有如下的性质:
如果 \(p \sim \operatorname{Beta}(t | \alpha, \beta)\),则: \[ E(p) =\frac{\alpha}{\alpha+\beta} \] 如果 \(\vec{p} \sim \operatorname{Dir}(\vec{t} | \vec{\alpha})\),则: \[ E(\vec{p})=\left(\frac{\alpha_{1}}{\sum_{i=1}^{K} \alpha_{i}}, \frac{\alpha_{2}}{\sum_{i=1}^{K} \alpha_{i}}, \cdots, \frac{\alpha_{K}}{\sum_{i=1}^{K} \alpha_{i}}\right) \]
MCMC 和 Gibbs Sampling
在随机模拟方法(又称为蒙特卡洛方法)中,一个重要问题是给定一个概率分布 \(p(x)\),如何在计算机中生成它的样本。
一般而言,均匀分布 \(Uniform(0,1)\) 的样本是相对容易生成的,而常见的概率分布可以通过均匀分布变换得到。然而,当 \(p(x)\) 的形式很复杂,或 \(p(x)\) 是高维分布的时候,样本的生成就很困难了。
此时就需要一些更加复杂的随机模拟的方法来生成样本。本节将介绍两种常用的方法:MCMC(Markov Chain Monte Carlo)和 Gibbs Sampling 方法。
首先,我们需要了解马尔科夫链的平稳分布性质。
马氏链的数学定义如下: \[ P\left(X_{t+1}=x | X_{t}, X_{t-1}, \cdots\right)=P\left(X_{t+1}=x | X_{t}\right) \] 即状态转移的概率只依赖于前一个状态。
我们可以证明,迭代次数足够大时,马氏链(非周期,可无限状态且状态相通)将收敛到一个稳定的分布,该分布与初始状态无关,仅与概率转移矩阵有关。收敛后得到的变量均符合该分布,但并不独立。
该分布 \(\pi\) 称为马氏链的平稳分布。\(\pi\) 是方程 \(\pi P = \pi\) 的唯一非负解。
Markov Chain Monte Carlo
对于给定的概率分布 \(p(x)\),如果我们能构造一个转移矩阵为 \(P\) 的马氏链,使得该马氏链的平稳分布恰好是 \(p(x)\),那么该马氏链收敛后的序列都将是 \(p(x)\) 的样本。现在的问题是,我们如何构造转移矩阵 \(P\),使得平稳分布恰好是我们要的分布 \(p(x)\) 呢?
我们将使用下述定理来进行构造:
细致平稳条件:如果非周期马氏链的转移矩阵 \(P\) 和分布 \(\pi(x)\) 满足: \[ \pi(i) P_{i j}=\pi(j) P_{j i} \quad \text { for all } \quad i, j \]
- 则 \(\pi(x)\) 是马氏链的平稳分布
对于一个转移矩阵为 \(q(i,j)\) 的马氏链,通常情况下,细致平稳条件不成立: \[ p(i) q(i, j) \neq p(j) q(j, i) \]
我们可以引入一个 \(\alpha(i,j)\) ,使得: \[ p(i) q(i, j) \alpha(i, j)=p(j) q(j, i) \alpha(j, i) \]
我们可以取: \[ \alpha(i, j)=p(j) q(j, i) \quad \alpha(j, i)=p(i) q(i, j) \]
于是有: \[ p(i) \underbrace{q(i, j) \alpha(i, j)}_{Q^{\prime}(i, j)}=p(j) \underbrace{q(j, i) \alpha(j, i)}_{Q^{\prime}(j, i)} \]
于是我们把原来的马氏链改造成了具有转移矩阵 \(Q^\prime\) 的马氏链,其平稳分布即为 \(p(x)\)!
在改造 \(Q\) 的过程中引入的 \(\alpha(i,j)\) 称为接受率,可以理解为在原来的马氏链上,从状态 \(i\) 以 \(q(i,j)\) 的概率转跳到状态 \(j\) 的时候,我们以 \(\alpha(i,j)\) 的概率接受这个转移:
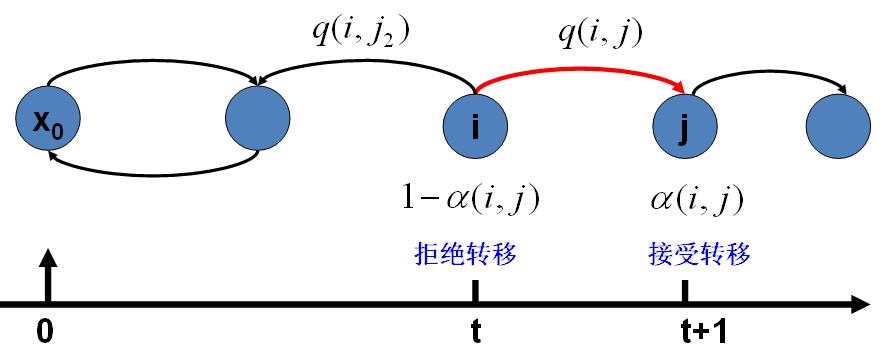
把以上过程整理一下,就可以得到用于采样概率分布 \(p(x)\) 的算法:
Algorithm MCMC 采样算法
- 初始化马氏链初始状态 \(X_0 = x_0\)
- 对 \(t=0,1,2,\cdots\),循环以下过程进行采样:
- 第 \(t\) 个时刻马氏链状态未 \(X_t = x_t\),采样 \(y \sim q\left(x | x_{t}\right)\)
- 从均匀分布采样 \(u \sim U n i f o r m[0,1]\)
- 如果 \(u<\alpha\left(x_{t}, y\right)=p(y) q\left(x_{t} | y\right)\),则接受转移 \(x_{t} \rightarrow y\),即 \(X_{t+1} = y\)
- 否则不接受转移,即 \(X_{t+1} = x_t\)
- 上述过程对连续分布以及高维空间均成立
上述算法存在一个小问题:马氏链在转移过程中的接受率 \(\alpha(i,j)\) 可能偏小,导致马氏链容易原地踏步,使得收敛到平稳分布的速度太慢。
注意到对于细致平稳条件来说,等式两边同时扩大并不会打破原有的等式,因此我们可以将 \(\alpha(i,j)\) 和 \(\alpha(i,j)\) 同比例放大,使得两数中最大的一个放大到 1: \[ \alpha(i, j)=\min \left\{\frac{p(j) q(j, i)}{p(i) q(i, j)}, 1\right\} \] 于是,我们得到了下面的 Metropolis-Hastings 算法:
Algorithm Metropolis-Hastings 采样算法
- 初始化马氏链初始状态 \(X_0 = x_0\)
- 对 \(t=0,1,2,\cdots\),循环以下过程进行采样:
- 第 \(t\) 个时刻马氏链状态为 \(X_t = x_t\),采样 \(y \sim q\left(x | x_{t}\right)\)
- 从均匀分布采样 \(u \sim U n i f o r m[0,1]\)
- 如果 \(u<\alpha\left(x_{t}, y\right)=\min \left\{\frac{p(y) q\left(x_{t} | y\right)}{p\left(x_{t}\right) p\left(y | x_{t}\right)}, 1\right\}\),则接受转移 \(x_{t} \rightarrow y\),即 \(X_{t+1} = y\)
- 否则不接受转移,即 \(X_{t+1} = x_t\)
Gibbs Sampling
对于高维的情形,由于接受率的存在(通常 \(\alpha < 1\)),上述算法的效率并不是很高,我们希望找到一个转移矩阵 \(Q\) 使得接受率 \(\alpha=1\)。
对于二维的情形,假设有一个概率分布 \(p(x,y)\),考察 \(x\) 坐标相同的两个点 \(A\left(x_{1}, y_{1}\right), B\left(x_{1}, y_{2}\right)\),可以发现: \[
\begin{array}{l}{p\left(x_{1}, y_{1}\right) p\left(y_{2} | x_{1}\right)=p\left(x_{1}\right) p\left(y_{1} | x_{1}\right) p\left(y_{2} | x_{1}\right)} \\ {p\left(x_{1}, y_{2}\right) p\left(y_{1} | x_{1}\right)=p\left(x_{1}\right) p\left(y_{2} | x_{1}\right) p\left(y_{1} | x_{1}\right)}\end{array}
\] 所以有: \[
p\left(x_{1}, y_{1}\right) p\left(y_{2} | x_{1}\right)=p\left(x_{1}, y_{2}\right) p\left(y_{1} | x_{1}\right)
\] 即: \[
p(A) p\left(y_{2} | x_{1}\right)=p(B) p\left(y_{1} | x_{1}\right)
\] 基于以上等式,我们发现在 \(x=x_1\) 这条平行于 \(y\) 轴的直线上,如果使用条件分布 \(p\left(y | x_{1}\right)\) 作为任意两个点之间的转移概率,那么任意两个点之间的转移满足细致平稳条件。该结论对于平行于 \(x\) 轴的直线也成立: \[
p(A) p\left(x_{2} | y_{1}\right)=p(C) p\left(x_{1} | y_{1}\right)
\] 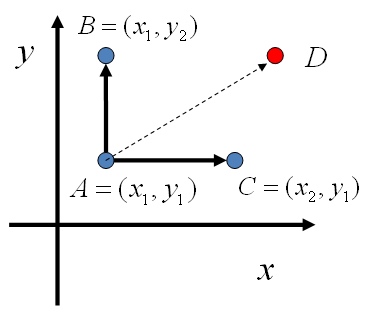
因此,我们可以构造如下平面上任意两点之间的转移概率矩阵 \(Q\) \[ \begin{array}{ll}{Q(A \rightarrow B)=p\left(y_{B} | x_{1}\right)} & {\text{if} \quad x_{A}=x_{B}=x_{1}} \\ {Q(A \rightarrow C)=p\left(x_{C} | y_{1}\right)} & {\text{if}\quad y_{A}=y_{C}=y_{1}} \\ {Q(A \rightarrow D)=0} & {\text {others}}\end{array} \] 基于上述转移矩阵 \(Q\),我们可以证明对于平面上任意两点 \(X,Y\),满足细致平稳条件: \[ p(X) Q(X \rightarrow Y)=p(Y) Q(Y \rightarrow X) \] 于是这个二维空间上的马氏链将收敛到平稳分布 \(p(x,y)\),而这个算法就称为 Gibbs Sampling 算法:
Algorithm 二维 Gibbs Sampling 算法
- 随机初始化 \(X_0 = x_0, Y_0 = y_0\)
- 对 \(t=0,1,2,\cdots\),循环采样:
- \(y_{t+1} \sim p\left(y | x_{t}\right)\)
- \(y_{t+1} \sim p\left(y | x_{t}\right)\)
以上采样过程中,马氏链的转义只是轮换地沿着坐标轴 \(x\) 轴和 \(y\) 轴作转移,最终收敛后得到的样本就是 \(p(x,y)\) 的样本。可以采用坐标轴轮换,也可以随机选择坐标轴转移。
上述过程可以推广到高维,即沿着单根坐标轴转移,以其他所有坐标轴为条件:
Algorithm n 维 Gibbs Sampling 算法
- 随机初始化 \(\left\{x_{i} : i=1, \cdots, n\right\}\)
- 对 \(t=0,1,2,\cdots\),循环采样:
- \(x_{1}^{(t+1)} \sim p\left(x_{1} | x_{2}^{(t)}, x_{3}^{(t)}, \cdots, x_{n}^{(t)}\right)\)
- \(x_{2}^{(t+1)} \sim p\left(x_{2} | x_{1}^{(t+1)}, x_{3}^{(t)}, \cdots, x_{n}^{(t)}\right)\)
- \(\cdots\)
- \(x_{j}^{(t+1)} \sim p\left(x_{j} | x_{1}^{(t+1)}, \cdots, x_{j-1}^{(t+1)}, x_{j+1}^{(t)}, \cdots, x_{n}^{(t)}\right)\)
- \(\cdots\)
- \(x_{n}^{(t+1)} \sim p\left(x_{n} | x_{1}^{(t+1)}, x_{2}^{t}, \cdots, x_{n-1}^{(t+1)}\right)\)
文本建模
在日常生活中存在着大量的文本,如果每一个文本存储为一篇文档,那每篇文档从人的观察来说就是有序的词的序列 \(d=\left(w_{1}, w_{2}, \cdots, w_{n}\right)\)。
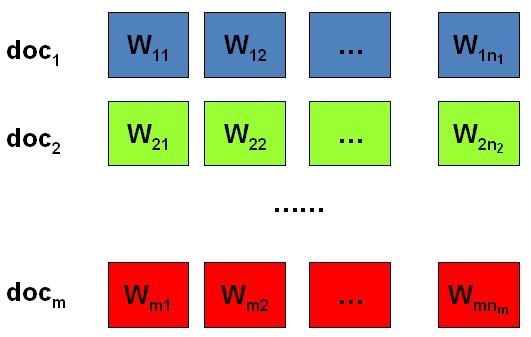
统计文本建模的目的就是追问这些观察到的语料库中的词序列是如何生成的。其核心的两个问题是:
- 模型中有哪些参数?
- 如何基于模型来产生词序列?
下面我们将介绍在 LDA 之前出现的两种文本建模的方法:Unigram Model 和 PLSA Model。
Unigram Model
假设我们的词典中一共有 \(V\) 个词,最简单的一种文本建模方式就是 Unigram Model,其方法如下:
Algorithm Unigram Model
- 上帝只有一个骰子,这个骰子有 \(V\) 个面,每个面对应一个词,各个面的概率不一
- 即参数为词典中每个词语出现的概率 \(\vec{p}=\left(p_{1}, p_{2}, \cdots, p_{V}\right)\)
- 该模型并不关心词语的顺序信息
- 每抛一次骰子,抛出的面就对应地产生一个词,假设总词频为 \(N\),则生成语料的方法为独立地抛 \(N\) 次骰子产生这 \(N\) 个词
基于上述方法,假定每个词 \(v_i\) 的发生次数为 \(n_i\),则 \(\vec{n}=\left(n_{1}, n_{2}, \cdots, n_{V}\right)\) 恰好为一个多项分布: \[ p(\vec{n})=\operatorname{Mult}(\vec{n} ;\vec{p}, N)=\left(\begin{array}{c}{N} \\ {\vec{n}}\end{array}\right) \prod_{k=1}^{V} p_{k}^{n_{k}} \] 则语料的产生概率为: \[ p(\mathcal{W})=p\left(\vec{w}_{1}\right) p\left(\vec{w}_{2}\right) \cdots p(\vec{w}_{m})=\prod_{k=1}^{V} p_{k}^{n_{k}} \] 参数的最大似然估计值为: \[ \hat{p}_{i}=\frac{n_{i}}{N} \] 上述方法假定参数 \(\vec{p}\) 是确定的,而从贝叶斯学派的角度看,一切参数都是随机变量。因此上述模型中的参数应该满足某个概率分布 \(p(\vec{p})\),该分布称为参数 \(\vec{p}\) 的先验分布。修改后的算法流程如下:
Algorithm Bayesian Unigram Model
- 上帝有一个装有无穷多个骰子的坛子,里面有各式各样的骰子,每个骰子有 \(V\) 个面
- 上帝从坛子里面抽了一个骰子出来,然后用这个骰子不断地抛,产生了语料中的所有的词
在上述假设下,语料的产生概率计算如下: \[ p(\mathcal{W})=\int p(\mathcal{W} | \vec{p}) p(\vec{p}) d \vec{p} \] 那么如何选择先验分布 \(p(\vec{p})\) 呢?注意到词语的发生次数满足多项分布,因此基于之前的结论,我们选择多项分布的共轭分布,即 Dirichlet 分布: \[ \operatorname{Dir}(\vec{p} | \vec{\alpha})=\frac{1}{\Delta(\vec{\alpha})} \prod_{k=1}^{V} p_{k}^{\alpha_{k}-1} \quad \vec{\alpha}=\left(\alpha_{1}, \cdots, \alpha_{V}\right) \] 其中: \[ \Delta(\vec{\alpha})=\int \prod_{k=1}^{V} p_{k}^{\alpha_{k}-1} d \vec{p} \] 可以通过下图理解 Dirichlet 先验下的 Unigram Model:
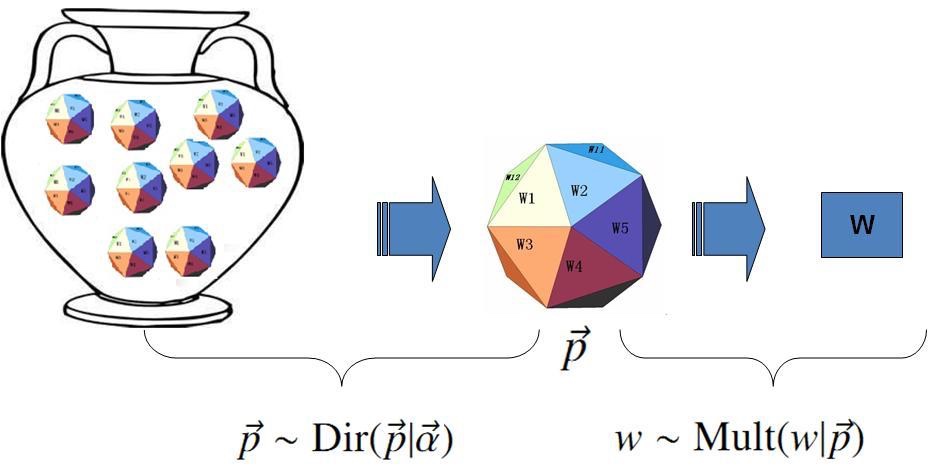
基于之前的结论,我们有如下等式: \[ \operatorname{Dir}(\vec{p} | \vec{\alpha})+\operatorname{Mult}(\vec{n})=\operatorname{Dir}(\vec{p} | \vec{\alpha}+\vec{n}) \] 因此后验分布为: \[ p(\vec{p} | \mathcal{W}, \vec{\alpha})=\operatorname{Dir}(\vec{p} | \vec{\alpha}+\vec{n})=\frac{1}{\Delta(\vec{n}+\vec{\alpha})} \prod_{k=1}^{V} p_{k}^{n_{k}+\alpha_{k}-1} d \vec{p} \] 在贝叶斯框架下,我们取参数在后验分布下的平均值作为参数的估计值,基于之前的结论,我们有: \[ E(\vec{p})=\left(\frac{n_{1}+\alpha_{1}}{\sum_{i=1}^{V}\left(n_{i}+\alpha_{i}\right)}, \frac{n_{2}+\alpha_{2}}{\sum_{i=1}^{V}\left(n_{i}+\alpha_{i}\right)}, \cdots, \frac{n_{V}+\alpha_{V}}{\sum_{i=1}^{V}\left(n_{i}+\alpha_{i}\right)}\right) \] 进一步,我们可以计算语料的产生概率(基于先验分布和后验分布下的估计值计算)为: \[ \begin{aligned} p(\mathcal{W} | \vec{\alpha}) &=\int p(\mathcal{W} | \vec{p}) p(\vec{p} | \vec{\alpha}) d \vec{p} \\ &=\int \prod_{k=1}^{V} p_{k}^{n_{k}} \operatorname{Dir}(\vec{p} | \vec{\alpha}) d \vec{p} \\ &=\int \prod_{k=1}^{V} p_{k}^{n_{k}} \frac{1}{\Delta(\vec{\alpha})} \prod_{k=1}^{V} p_{k}^{\alpha_{k}-1} d \vec{p} \\ &=\frac{1}{\Delta(\vec{\alpha})} \int \prod_{k=1}^{V} p_{k}^{n_{k}+\alpha_{k}-1} d \vec{p} \\ &=\frac{\Delta(\vec{n}+\vec{\alpha})}{\Delta(\vec{\alpha})} \end{aligned} \]
PLSA Model
PLSA(Probabilistic Latent Semantic Analysis) Model 相比于 Unigram Model,引入了主题(Topic)的概念。PLSA Model 认为一篇文档可以由多个主题混合而成,而每个主题都是词汇上的概率分布,文档中的每个词都是由一个固定的主题生成的。
基于上述概念,PLSA Model 的流程如下:
Algorithm PLSA Model
- 上帝有两种类型的骰子
- 一类是 doc-topic 骰子,每个 doc-topic 骰子有 K 个面,每个面是一个 topic 的编号
- 一类是 topic-word 骰子,每个 topic-word 骰子有 \(V\) 个面,每个面对应一个词
- 上帝共有 \(K\) 个 topic-word 骰子,每个骰子都有一个编号,编号从 \(1\) 到 \(K\)
- 生成每篇文档之前,上帝都先为这篇文章制造一个特定的 doc-topic 骰子,然后重复如下过程生成文档中的词:
- 投掷这个 doc-topic 骰子,得到一个 topic 编号 \(z\)
- 选择 \(K\) 个 topic-word 骰子中编号为 \(z\) 的那个,投掷这个骰子,于是得到一个词
上述过程可以用下图表示:
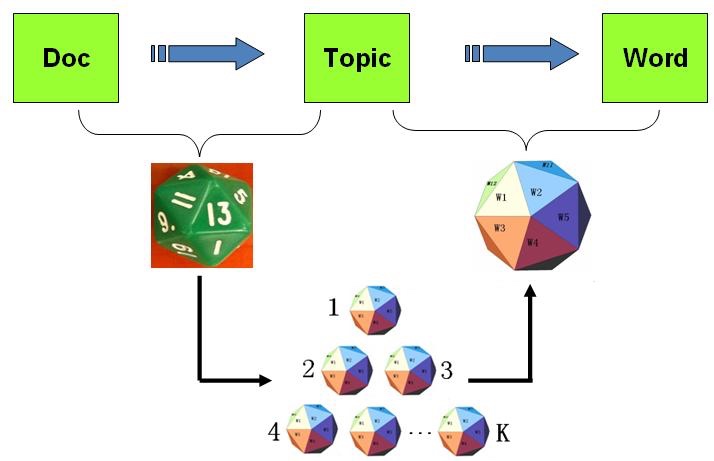
该模型的数学表达如下:
游戏中的 \(K\) 个 topic-word 骰子记为 \(\vec{\varphi}_{1}, \cdots, \vec{\varphi}_{K}\)
对于包含 \(M\) 篇文档的语料 \(C=\left(d_1,d_2,\cdots,d_M\right)\) 中的每篇文档 \(d_m\),都会有一个特定的 doc-topic 骰子 \(\vec{\theta}_m\)
- 所有对应的骰子记为 \(\vec{\theta}_1,\cdots, \vec{\theta}_M\)
在 PLSA Model 中,第 \(m\) 篇文档 \(d_m\) 中的每个词的生成概率为: \[ p\left(w | d_{m}\right)=\sum_{z=1}^{K} p(w | z) p\left(z | d_{m}\right)=\sum_{z=1}^{K} \varphi_{z w} \theta_{m z} \]
因此整篇文档的生成概率为: \[ p\left(\vec{w} | d_{m}\right)=\prod_{i=1}^{n} \sum_{z=1}^{K} p\left(w_{i} | z\right) p\left(z | d_{m}\right)=\prod_{i=1}^{n} \sum_{z=1}^{K} \varphi_{z w_{i}} \theta_{d z} \]
求解上述模型中的参数可以使用 EM 算法(因为包含隐含变量 \(z\)),这里不作展开。
LDA 文本建模
对于 PLSA Model,doc-topic 骰子 \(\vec{\theta}_m\) 和 topic-word 骰子 \(\vec{\varphi}_m\) 都是模型中的参数,但并没有看作随机变量。如果使用贝叶斯学派的观点,将上述参数看作随机变量,为其添加先验分布,即可将 PLSA 对应的游戏过程改造为一个贝叶斯的游戏过程。
由于 \(\vec{\theta}_m\) 和 \(\vec{\varphi}_m\) 都对应到多项分布,所以先验分布的一个好的选择就是 Dirichlet 分布,于是我们就得到了 LDA(Latent Dirichlet Allocation)模型。
Algorithm LDA Model
- 上帝有两大坛子的骰子,第一个坛子装的是 doc-topic 骰子,第二个坛子装的是 topic-word 骰子
- 上帝随机地从第二个坛子中独立地抽取了 \(K\) 个 topic-word 骰子,编号为 \(1\) 到 \(K\)
- 每次生成一篇新的文档前,上帝先从第一个坛子中随机抽取一个 doc-topic 骰子,然后重复如下过程生成文档中的词:
- 投掷这个 doc-topic 骰子,得到一个 topic 编号 \(z\)
- 选择 \(K\) 个 topic-word 骰子中编号为 \(z\) 的那个,投掷这个骰子,于是得到一个词
上述过程可以用下图表示:
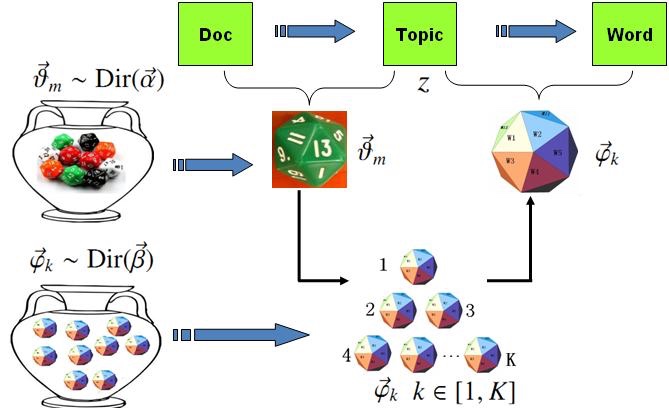
假设语料库中有 \(M\) 篇文档,所有的 word 和对应的 topic 如下表示: \[ \begin{aligned} \vec{\mathbf{w}} &=\left(\vec{w}_{1}, \cdots, \vec{w}_{M}\right) \\ \vec{\mathbf{z}} &=\left(\vec{z}_{1}, \cdots, \vec{z}_{M}\right) \end{aligned} \]
- \(\vec{w}_m\) 表示第 \(m\) 篇文档中的词
- \(\vec{z}_m\) 表示这些词对应的 topic 编号
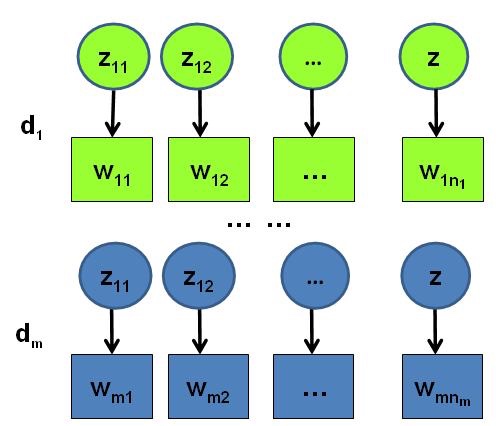
物理过程分解
我们可以将 LDA 模型的游戏过程用如下概率图模型表示:
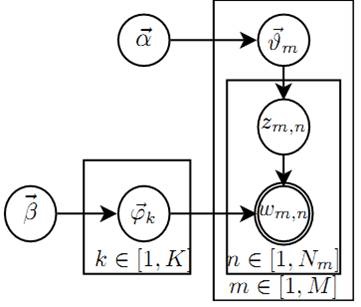
该概率图可以分解为两个主要的物理过程:
- \(\vec{\alpha} \rightarrow \vec{\theta}_{m} \rightarrow z_{m, n}\),这个过程表示在生成第 \(m\) 篇文档的时候,先从第一个坛子抽了一个 doc-topic 骰子 \(\vec{\theta}_m\),然后投掷这个骰子生成了文档中第 \(n\) 个词的 topic 编号 \(z_{m,n}\)
- \(\vec{\beta} \rightarrow \vec{\varphi}_{k} \rightarrow w_{m, n} | k=z_{m, n}\),这个过程表示在上帝手头的 \(K\) 个 topic-word 骰子 \(\vec{\varphi}_k\) 中,挑选编号为 \(k=z_{m,n}\) 的那个骰子进行投掷,然后生成 word \(w_{m,n}\)
在 LDA 模型中,有一些物理过程是相互独立可交换的,\(M\) 篇文档会对应 \(M\) 个独立的 Dirichlet-Multinomial 共轭结构,\(K\) 个 topic 会对应 \(K\) 个独立的 Dirichlet-Multinomial 共轭结构,因此 LDA 模型可以被分解为 \(M+K\) 个 Dirichlet-Multinomial 共轭结构,下面我们来具体阐述这两个结构。
M 个 Dirichlet-Multinomial 共轭结构
对于第一个物理过程,\(\vec{\alpha} \rightarrow \vec{\theta}_{m} \rightarrow \vec{z}_{m}\) 表示生成第 \(m\) 篇文档中所有词对应的 topics,显然 \(\vec{\alpha} \rightarrow \vec{\theta}_{m}\) 对应于 Dirichlet 分布,\(\vec{\theta}_{m} \rightarrow \vec{z}_{m}\) 对应于 Multinomial 分布,所以该过程整体是一个 Dirichlet-Multinomial 结构: \[ \vec{\alpha} \underbrace{\longrightarrow}_{\text {Dirichlet }} \vec{\theta}_{m} \underbrace{\longrightarrow}_{\text {Multinomial }} \vec{z}_{m} \] 利用 Dirichlet-Multinomial 共轭结构,我们得到参数 \(\vec{\theta}_m\) 的后验分布恰好是: \[ \operatorname{Dir}\left(\vec{\theta}_{m} | \vec{n}_{m}+\vec{\alpha}\right) \] 基于之前 Bayesian Unigram Model 中的计算结果,我们可以得到: \[ p\left(\vec{z}_{m} | \vec{\alpha}\right)=\frac{\Delta\left(\vec{n}_{m}+\vec{\alpha}\right)}{\Delta(\vec{\alpha})} \]
- 其中 \(\vec{n}_{m}=\left(n_{m}^{(1)}, \cdots, n_{m}^{(K)}\right)\) 表示第 \(m\) 篇文档中不同 topic 产生的词的个数(总数为该篇文档的词语数)
由于语料中 \(M\) 篇文档的 topics 生成过程相互独立,所以我们得到了 \(M\) 个相互独立的 Dirichlet-Multinomial 共轭结构,从而可以得到整个语料中 topics 的生成概率: \[ \begin{aligned} p(\vec{\mathbf{z}} | \vec{\alpha}) &=\prod_{m=1}^{M} p\left(\vec{z}_{m} | \vec{\alpha}\right) \\ &=\prod_{m=1}^{M} \frac{\Delta\left(\vec{n}_{m}+\vec{\alpha}\right)}{\Delta(\vec{\alpha})} \end{aligned} \]
K 个 Dirichlet-Multinomial 共轭结构
为了得到这 \(K\) 个共轭结构,我们需要对游戏的顺序作如下调整:
Algorithm LDA Model 2
- 上帝有两大坛子的骰子,第一个坛子装的是 doc-topic 骰子,第二个坛子装的是 topic-word 骰子
- 上帝随机地从第二个坛子中独立地抽取了 \(K\) 个 topic-word 骰子,编号为 \(1\) 到 \(K\)
- 每次生成一篇新的文档前,上帝先从第一个坛子中随机抽取一个 doc-topic 骰子,然后重复投掷这个 doc-topic 骰子,为每个词生成一个 topic 编号 \(z\)
- 重复如上过程处理每篇文档,生成语料中每个词的 topic 编号,但是词尚未生成
- 从头到尾,对语料中的每篇文档中的每个 topic 编号 \(z\),选择 \(K\) 个 topic-word 骰子中编号为 \(z\) 的那个,投掷这个骰子,于是生成对应的 word
以上游戏是先生成了语料中所有词的 topic,然后对每个词在给定 topic 的条件下生成 word。由于使用的是词袋模型,词语之间的顺序信息并没有被考虑,所以上述过程与之前的游戏是等价的。于是我们把具有相同 topic 的词归类: \[ \begin{aligned} \overrightarrow{\mathbf{w}}^{\prime} &=\left(\vec{w}_{(1)}, \cdots, \vec{w}_{(K)}\right) \\ \overrightarrow{\mathbf{z}}^{\prime} &=\left(\vec{z}_{(1)}, \cdots, \vec{z}_{(K)}\right) \end{aligned} \]
- \(\vec{w}_{(k)}\) 表示这些词都是由第 \(k\) 个 topic 生成的
- \(\vec{z}_{(k)}\) 对应于这些词的 topic 编号,所以 \(\vec{z}_{(k)}\) 中的分量都是 \(k\)
对于第二个物理过程,考虑如下过程 \(\vec{\beta} \rightarrow \vec{\varphi}_{k} \rightarrow \vec{w}_{(k)}\),此时 \(\vec{\beta} \rightarrow \vec{\varphi}_{k}\) 对应于 Dirichlet 分布,\(\vec{\varphi}_{k} \rightarrow \vec{w}_{(k)}\) 对应于 Multinomial 分布,所以整体也是一个 Dirichlet-Multinomial 共轭结构: \[ \vec{\beta} \underbrace{\longrightarrow}_{\text {Dirichlet }} \vec{\varphi}_{k} \underbrace{\longrightarrow}_{\text {Multinomial }} \vec{w}_{(k)} \] 类似地,我们得到参数 \(\vec{\varphi}_{k}\) 的后验分布恰好是: \[ \operatorname{Dir}\left(\vec{\varphi}_{k} | \vec{n}_{k}+\vec{\beta}\right) \] 同理,我们可以得到: \[ p\left(\vec{w}_{(k)} | \vec{\beta}\right)=\frac{\Delta\left(\vec{n}_{k}+\vec{\beta}\right)}{\Delta(\vec{\beta})} \]
- 其中 \(\vec{n}_{k}=\left(n_{k}^{(1)}, \cdots, n_{k}^{(V)}\right)\) 表示第 \(k\) 个 topic 产生的词中不同词语的个数(总数为第 \(k\) 个 topic 产生的词语总数,取决于上一步)
由于语料中 \(K\) 个 topics 生成 words 的过程相互独立,所以我们得到 \(K\) 个相互独立的 Dirichlet-Multinomial 共轭结构,从而得到整个语料库中词生成概率: \[ \begin{aligned} p(\overrightarrow{\mathbf{w}} | \overrightarrow{\mathbf{z}}, \vec{\beta}) &=p\left(\overrightarrow{\mathbf{w}}^{\prime} | \overrightarrow{\mathbf{z}}^{\prime}, \vec{\beta}\right) \\ &=\prod_{k=1}^{K} p\left(\vec{w}_{(k)} | \vec{z}_{(k)}, \vec{\beta}\right) \\ &=\prod_{k=1}^{K} \frac{\Delta\left(\vec{n}_{k}+\vec{\beta}\right)}{\Delta(\vec{\beta})} \end{aligned} \] 将上述两个过程结合起来,得到: \[ \begin{aligned} p(\vec{\mathbf{w}}, \vec{\mathbf{z}} | \vec{\alpha}, \vec{\beta}) &=p(\vec{\mathbf{w}} | \vec{\mathbf{z}}, \vec{\beta}) p(\vec{\mathbf{z}} | \vec{\alpha}) \\ &=\prod_{k=1}^{K} \frac{\Delta(\vec{n}_{k}+\vec{\beta})}{\Delta(\vec{\beta})} \prod_{m=1}^{M} \frac{\Delta(\vec{n}_{m}+\vec{\alpha})}{\Delta(\vec{\alpha})} \end{aligned} \]
Gibbs Sampling
得到了联合分布 \(p(\vec{\mathbf{w}}, \vec{\mathbf{z}})\) 之后,我们可以使用 Gibbs Sampling 对这个分布进行采样。由于 \(\vec{w}\) 是观测到的已知数据,只有 \(\vec{z}\) 是隐含变量,因此真正需要采样的是分布 \(p(\vec{z} |\vec{w} )\)。
为了更好地理解采样过程,本节我们将基于 Dirichlet-Multinomial 共轭来推导 Gibbs Sampling 公式。
语料库 \(\vec{z}\) 中的第 \(i\) 个词对应的 topic 记为 \(z_i\),其中 \(i=(m,n)\) 是一个二维下标,对应于第 \(m\) 篇文档的第 \(n\) 个词,我们用 \(\neg i\) 表示去除下标为 \(i\) 的词。
按照 Gibbs Sampling 算法(高维)的要求,我们要求得任意一个坐标轴 \(i\) 对应的条件分布 \(p\left(z_{i}=k | \vec{\mathbf{z}}_{\neg i}, \vec{\mathbf{w}}\right)\),假设已经观测到的词 \(w_i=t\),则由贝叶斯法则,我们容易得到: \[ p\left(z_{i}=k | \vec{\mathbf{z}}_{\neg i}, \vec{\mathbf{w}}\right) \propto p\left(z_{i}=k, w_{i}=t | \vec{\mathbf{z}}_{\neg i}, \vec{\mathbf{w}}_{\neg i}\right) \] 由于 \(z_{i}=k, w_{i}=t\) 只涉及第 \(m\) 篇文档和 第 \(k\) 个 topic,所以上式的条件概率计算中,实际上也只会涉及到如下两个 Dirichlet-Multinomial 共轭结构:
- \(\vec{\alpha} \rightarrow \vec{\theta}_{m} \rightarrow \vec{z}_{m}\)
- \(\vec{\beta} \rightarrow \vec{\varphi}_{k} \rightarrow \vec{w}_{(k)}\)
另一方面,在语料中去掉第 \(i\) 个词对应的 \((z_i,w_i)\),并不改变我们之前讨论的 \(M+K\) 个共轭结构,只是某些地方的计数会变少。所以其后验分布为: \[ \begin{array}{l}{p\left(\vec{\theta}_{m} | \overrightarrow{\mathbf{z}}_{\neg i}, \overrightarrow{\mathbf{w}}_{\neg i}\right)=\operatorname{Dir}\left(\vec{\theta}_{m} | \vec{n}_{m,\neg i}+\vec{\alpha}\right)} \\ {p\left(\vec{\varphi}_{k} | \overrightarrow{\mathbf{z}}_{\neg i}, \overrightarrow{\mathbf{w}}_{\neg i}\right)=\operatorname{Dir}\left(\vec{\varphi}_{k} | \vec{n}_{k,\neg i}+\vec{\beta}\right)}\end{array} \] 基于上面的想法,通过一系列推导,可以得出如下的 Gibbs Sampling 公式: \[ \begin{aligned} p\left(z_{i}=k | \vec{\mathbf{z}}_{\neg i}, \vec{\mathbf{w}}\right) & \propto p\left(z_{i}=k, w_{i}=t | \vec{\mathbf{z}}_{\neg i}, \vec{\mathbf{w}}_{\neg i}\right) \\ &=\hat{\theta}_{m k} \cdot \hat{\varphi}_{k t} \end{aligned} \] 最终得到的结果就是对应的两个 Dirichlet 后验分布在贝叶斯框架下的参数估计,基于之前的公式,我们有: \[ \begin{aligned} \hat{\theta}_{m k} &=\frac{n_{m,\neg{i}}^{(k)}+\alpha_{k}}{\sum_{k=1}^{K}\left(n_{m,\neg{i}}^{(t)}+\alpha_{k}\right)} \\ \hat{\varphi}_{k t} &=\frac{n_{k,\neg{i}}^{(t)}+\beta_{t}}{\sum_{t=1}^{V}\left(n_{k,\neg{i}}^{(t)}+\beta_{t}\right)} \end{aligned} \] 于是,我们得到了如下 LDA 模型的 Gibbs Sampling 公式: \[ p\left(z_{i}=k | \vec{\mathbf{z}}_{\neg i}, \vec{\mathbf{w}}\right) \propto \frac{n_{m,\neg{i}}^{(k)}+\alpha_{k}}{\sum_{k=1}^{K}\left(n_{m,\neg{i}}^{(t)}+\alpha_{k}\right)} \cdot \frac{n_{k,\neg{i}}^{(t)}+\beta_{t}}{\sum_{t=1}^{V}\left(n_{k,\neg{i}}^{(t)}+\beta_{t}\right)} \] 由于 topic 有 \(K\) 个,所以 Gibbs Sampling 公式的物理意义其实就是在这 \(K\) 条路径中进行采样。
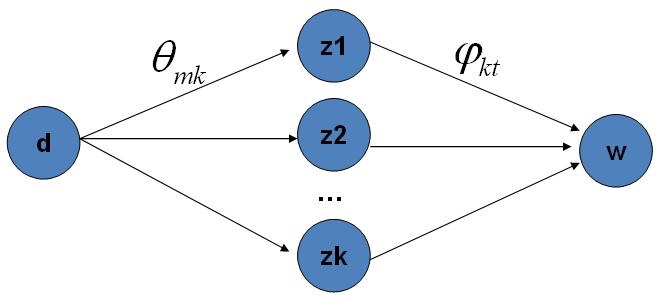
Training and Inference
对于 LDA 模型,我们的目标有两个:
- 估计模型中的参数 \(\vec{\varphi}_{1}, \cdots, \vec{\varphi}_{K}\) 和 \(\vec{\theta}_{1}, \cdots, \vec{\theta}_{M}\)
- 对于新来的一篇文档,能够计算这篇文档的 topic 分布 \(\vec{\theta}_{new}\)
训练 LDA 模型的过程是通过 Gibbs Sampling 获取语料中的 \((z,w)\) 的样本,模型中的所有参数都可以基于最终采样得到的样本进行估计。具体流程如下:
Algorithm LDA Training
- 随机初始化:对语料中每篇文档中的每个词 \(w\),随机地赋一个 topic 编号 \(z\)
- 重新扫描语料库,对每个词 \(w\) ,基于 Gibbs Sampling 公式重新采样其 topic,在语料库中进行更新
- 重复以上语料库的重新采样过程直到 Gibbs Sampling 收敛
- 统计语料库的 topic-word 共现频率矩阵,该矩阵就是 LDA 的模型
根据上述频率矩阵我们可以算出模型参数 \(\vec{\varphi}_{1}, \cdots, \vec{\varphi}_{K}\) 与 \(\vec{\theta}_{1}, \cdots, \vec{\theta}_{M}\),而在实际应用中,参数 \(\vec{\theta}\) 和训练语料中的每篇文档相关,对于理解新的文档并无用处,所以工程上最终存储 LDA 模型的时候一般没有必要保留。
通常,在 LDA 模型训练的过程中,我们是取 Gibbs Sampling 收敛之后的 \(n\) 个迭代的结果进行平均来做参数估计,这样模型质量更高。
有了 LDA 模型,对于新来的文档,我们只要认为 Gibbs Sampling 公式中的 \(\hat{\varphi}_{k t}\) 部分是稳定不变的,由训练语料得到的模型提供,采样过程中只需要估计该文档的 topic 分布 \(\vec{\theta}_{new}\) 即可。
Algorithm LDA Inference
- 随机初始化:对当前文档中的每个词 \(w\),随机地赋一个 topic 编号 \(z\)
- 重新扫描当前文档,按照 Gibbs Sampling 公式,对每个词 \(w\),重新采样它的 topic
- 重复以上过程直到 Gibbs Sampling 收敛
- 统计文档中的 topic 分布,该分布就是 \(\vec{\theta}_{new}\)