Transformer 原理解析

发表于 2019-11-01 分类于人工智能，文章精读阅读次数：本文字数： 2.9k 阅读时长 ≈ 10 分钟

本篇博客为对 Transformer 原始论文（ Attention Is All You Need ）的解读。

对于序列模型，传统的神经网络结构存在着难以处理长期依赖和计算效率低等问题。尽管研究者们提出了 LSTM、注意力机制、CNN 结合 RNN 等手段，但仍无法有效解决这些问题。Transformer 是一种新的神经网络结构，其仅基于注意力机制，抛弃了传统的循环或卷积神经网络结构。

Model Architecture

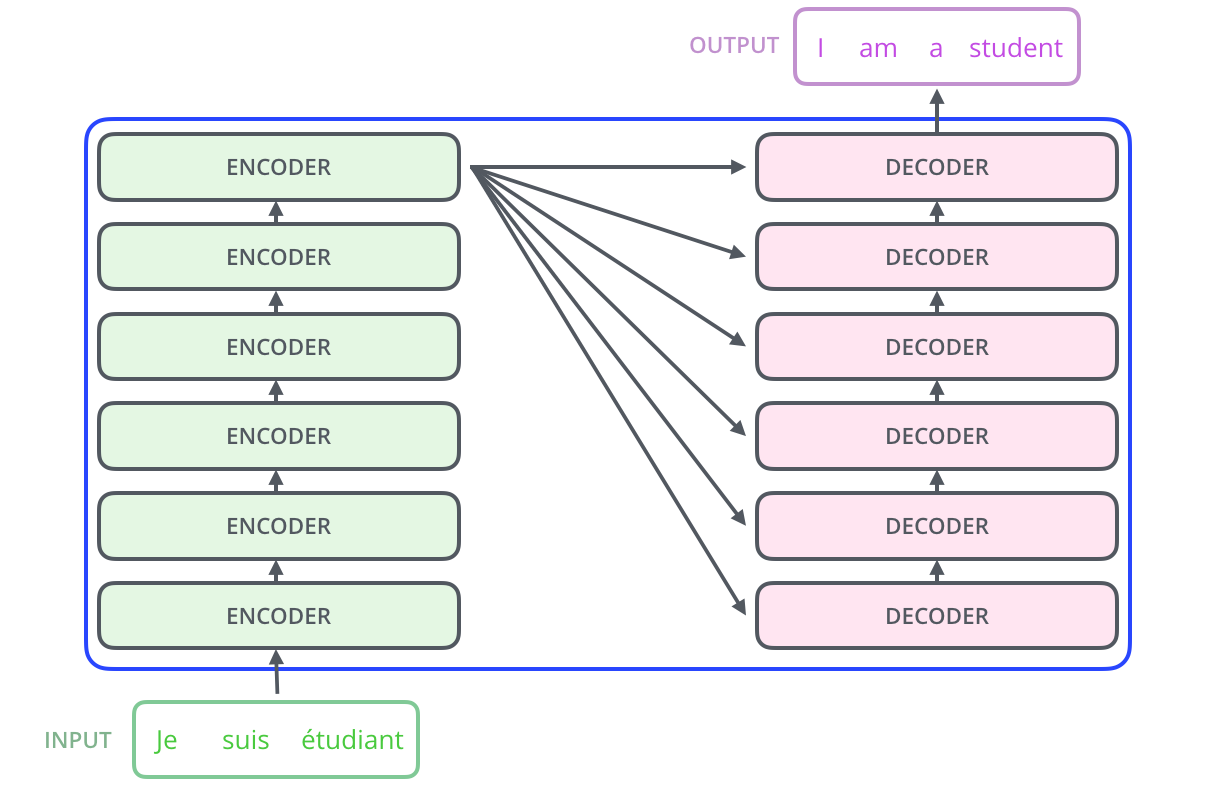
Transformer 基于现有的序列-序列模型，使用 encoder-decoder 架构。在 encoder-decoder 架构中，编码器（encoder）将输入序列 \((x_1, \ldots,x_n)\) 转换为一个连续的表达 \(\mathbf{z}=\left(z_{1}, \dots, z_{n}\right)\) ，然后解码器再基于该表达生成输出序列 \((y_1, \ldots, y_m)\)。

基于该架构，模型的整体结构如下图所示：

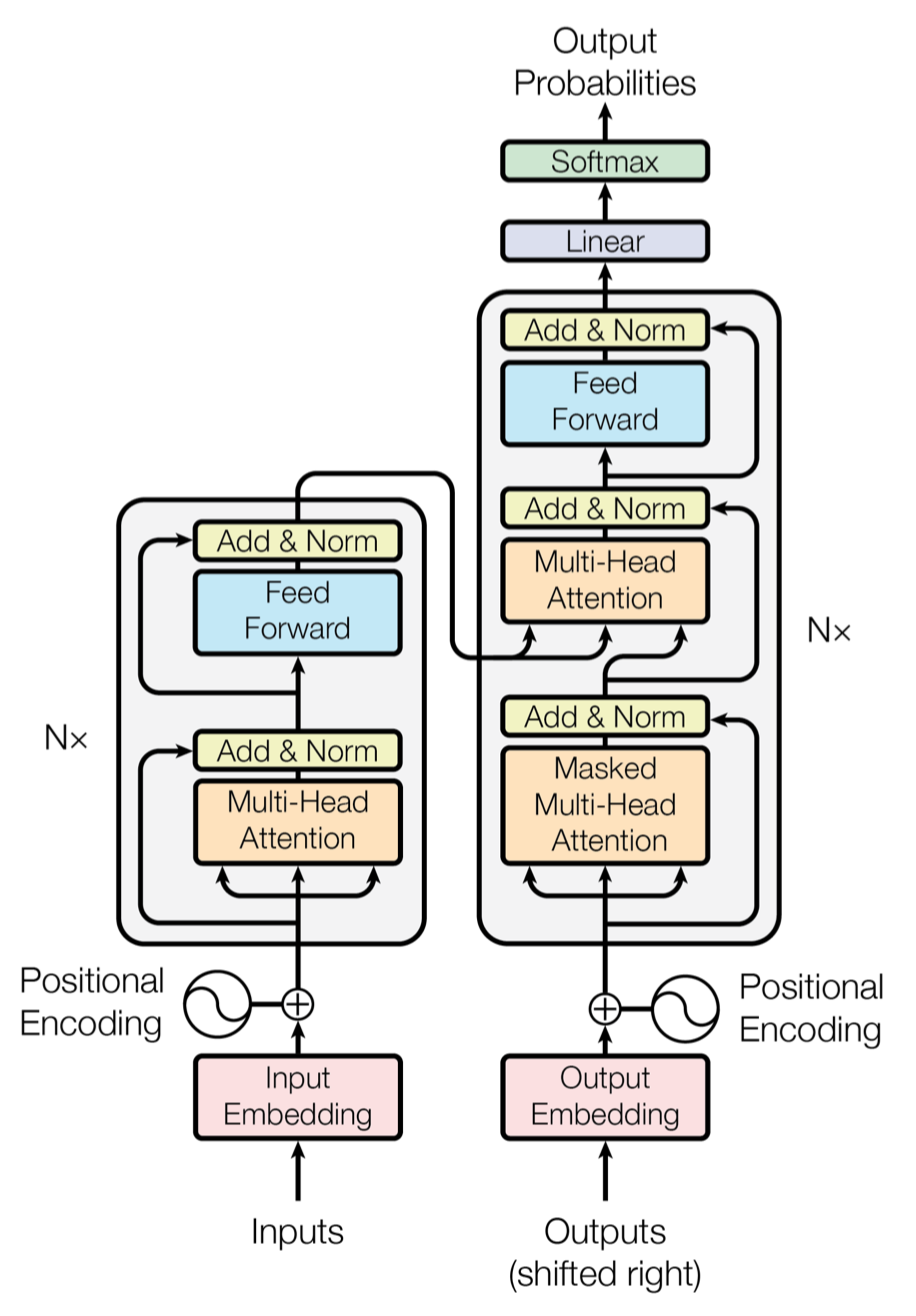
Encoder and Decoder Stacks

模型由 encoder 和 decoder 堆叠而成，每一层的具有相同的结构，如下图所示：

Encoder

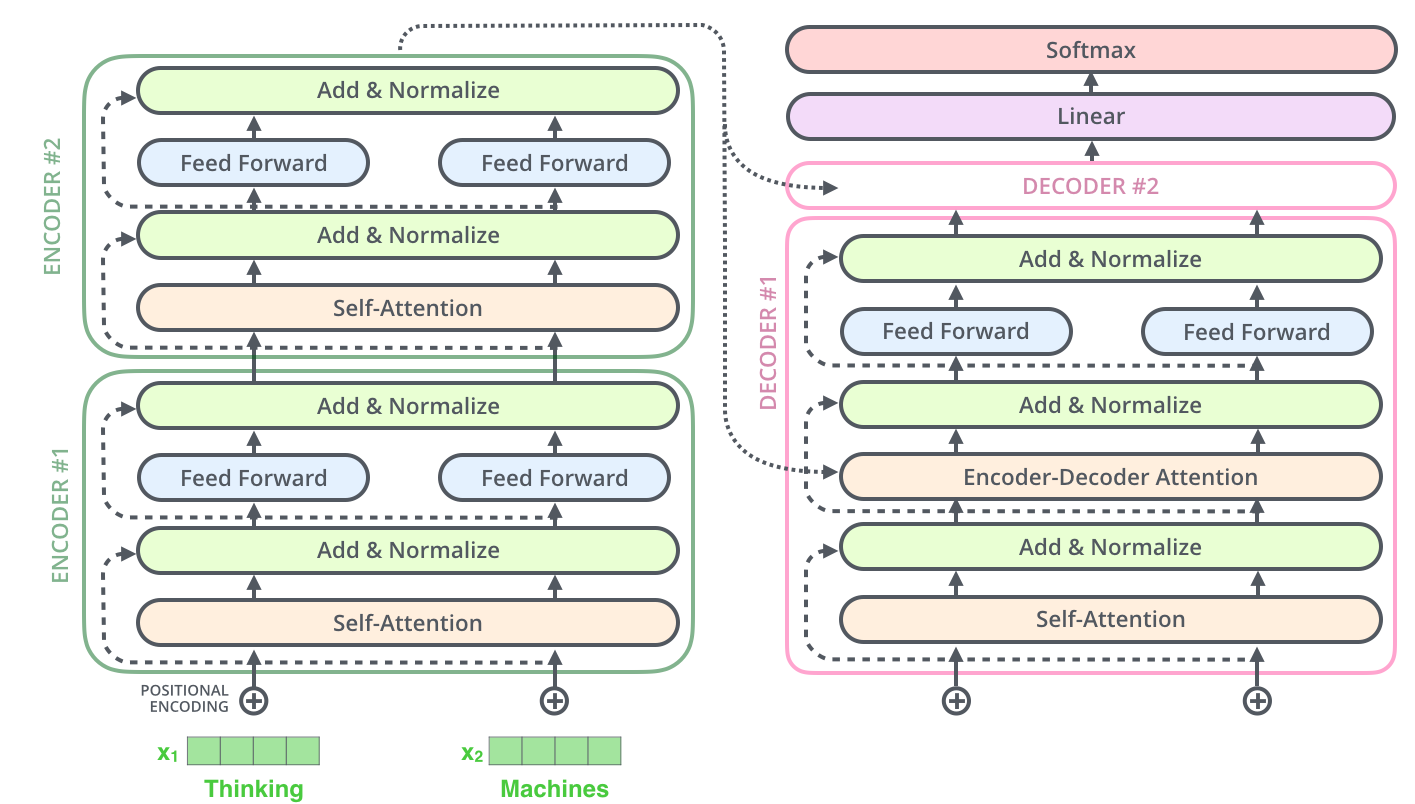
由 6 层组成，每一层包括两个子层：第一层是 multi-head self-attention 层，第二层是一个简单的全连接前馈网络。在每个子层后，都接了一个残差连接以及归一化，即每个子层的输出为 \(\text { LayerNorm }(x+\text { Sublayer }(x))\). 为了方便残差连接，模型中的所有子层，包括 embedding 层（初始词嵌入），输出向量维度均为 \(d_{\text{model}} = 512\).

Decoder

同样由 6 层组成，每一层包括三个子层：第一层是 masked multi-head self-attention 层，注意其输入仅包含当前位置之前的词语信息，这样设计的目的是解码器是按顺序解码的，其当前输出只能基于已输出的部分。第二层是 multi-head self-attention 层，其输入包含编码器的输出信息（矩阵 K 和矩阵 V ），第三层是全连接前馈网络。每个子层后同样加入了残差连接和归一化。下图给出了编码器和解码器的内部结构，注意前馈神经网络对于序列每个位置的独立性。

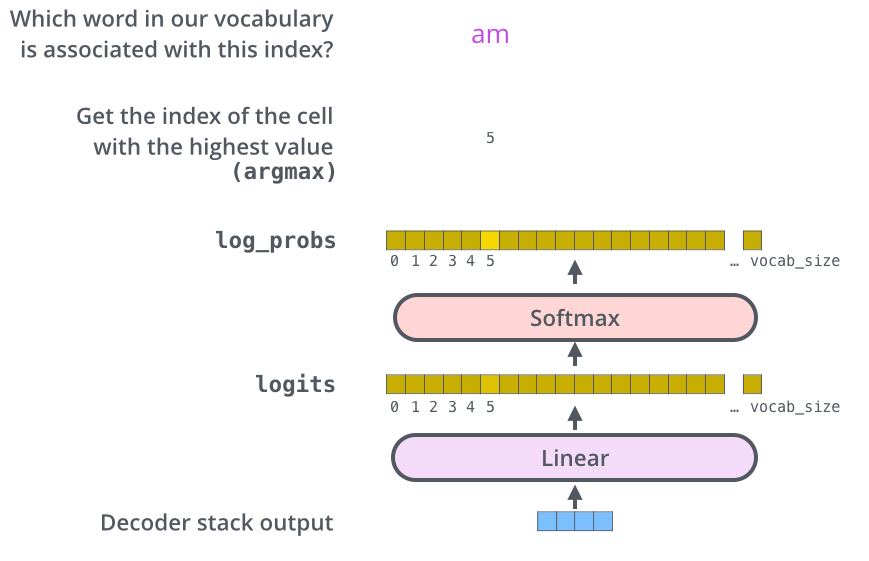
Linear and Softmax Layer

解码器的输出被输入到一个线性层中，转化为一个超长向量（词典长度），再输入到 softmax 层中转化为概率，最后运用适当策略（如贪婪搜索或束搜索）选择输出的词语，注意一次只输出一个词语。已输出的序列会作为解码器的输入。下图给出了贪婪搜索策略下的运行流程。

Attention

下面对模型中使用的 attention 机制进行解读。

Scaled Dot-Product Attention

Transformer 中使用的注意力机制被称为 ”Scaled Dot-Product Attention“。该机制的示意图如下所示。该模块的输入包括三个向量：查询向量 Q、键向量 K 和值向量 V。三个向量均基于输入向量计算得出（最初的输入向量为词嵌入），查询向量和键向量的维数为 \(d_k\)，值向量的维数为 \(d_v\)。我们先计算单个查询向量和所有键向量的点积，然后将其除以 \(\sqrt{d_k}\)，最后通过一个 softmax 函数得到对应的权重，再与值向量进行加权。

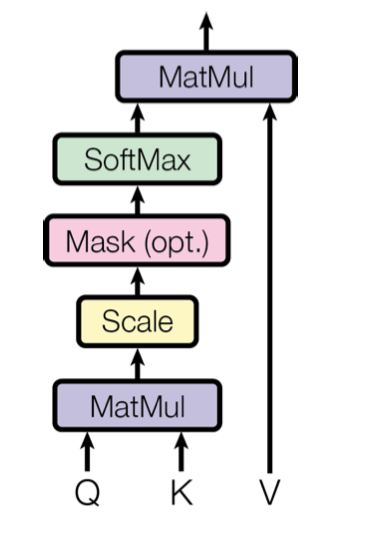
上述过程可以通过下图进行理解。其中除以 \(\sqrt{d_k}\) 进行的缩放操作的目的是提供更稳定的梯度，便于之后的训练。简单来说，该模块将一个输入向量转化为了一个包含其他位置权重的向量。

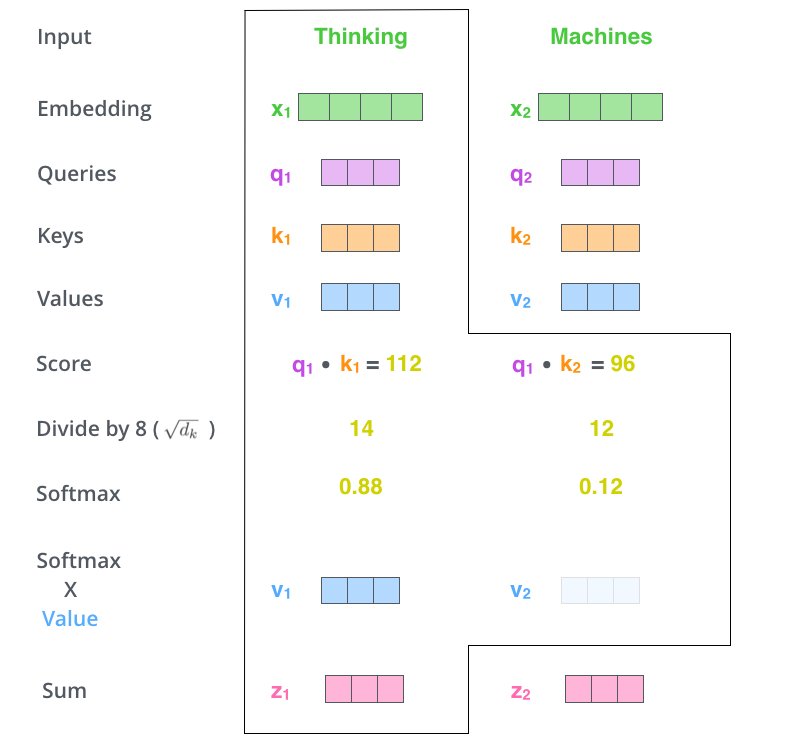
在实际应用中，我们会基于矩阵来进行并行计算，该过程可以表达为如下公式： \[ \text { Attention }(Q, K, V)=\operatorname{softmax}\left(\frac{Q K^{T}}{\sqrt{d_{k}}}\right) V \tag{1} \]

Multi-Head Attention

研究人员发现，比起使用一个注意力函数得到 \(d_{\text{model}}\) 维数的值向量，并行地训练多个值向量，再将它们拼接在一起得到输出效果更好。上述思想即 Transformer 中的 Multi-Head Attention，如下图所示。

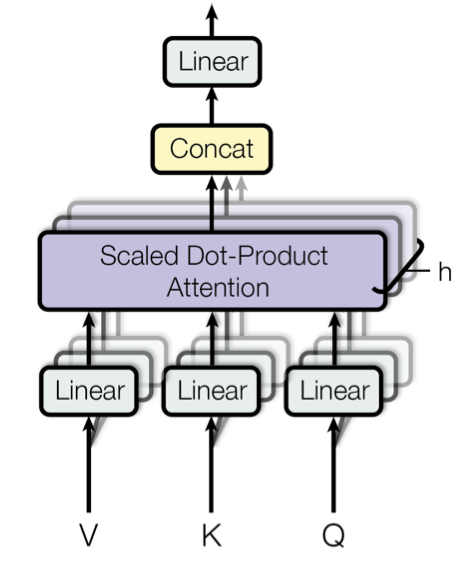
具体来说，给定一个输入矩阵，我们基于不同的参数矩阵计算得到多组 V、K、Q 矩阵，然后通过多个注意力函数计算得出多个加权后的 V 矩阵，最后将这些矩阵拼接起来，通过一个权重矩阵 \(W^{O}\) 得到最终的输出。下图描绘出了整个流程。

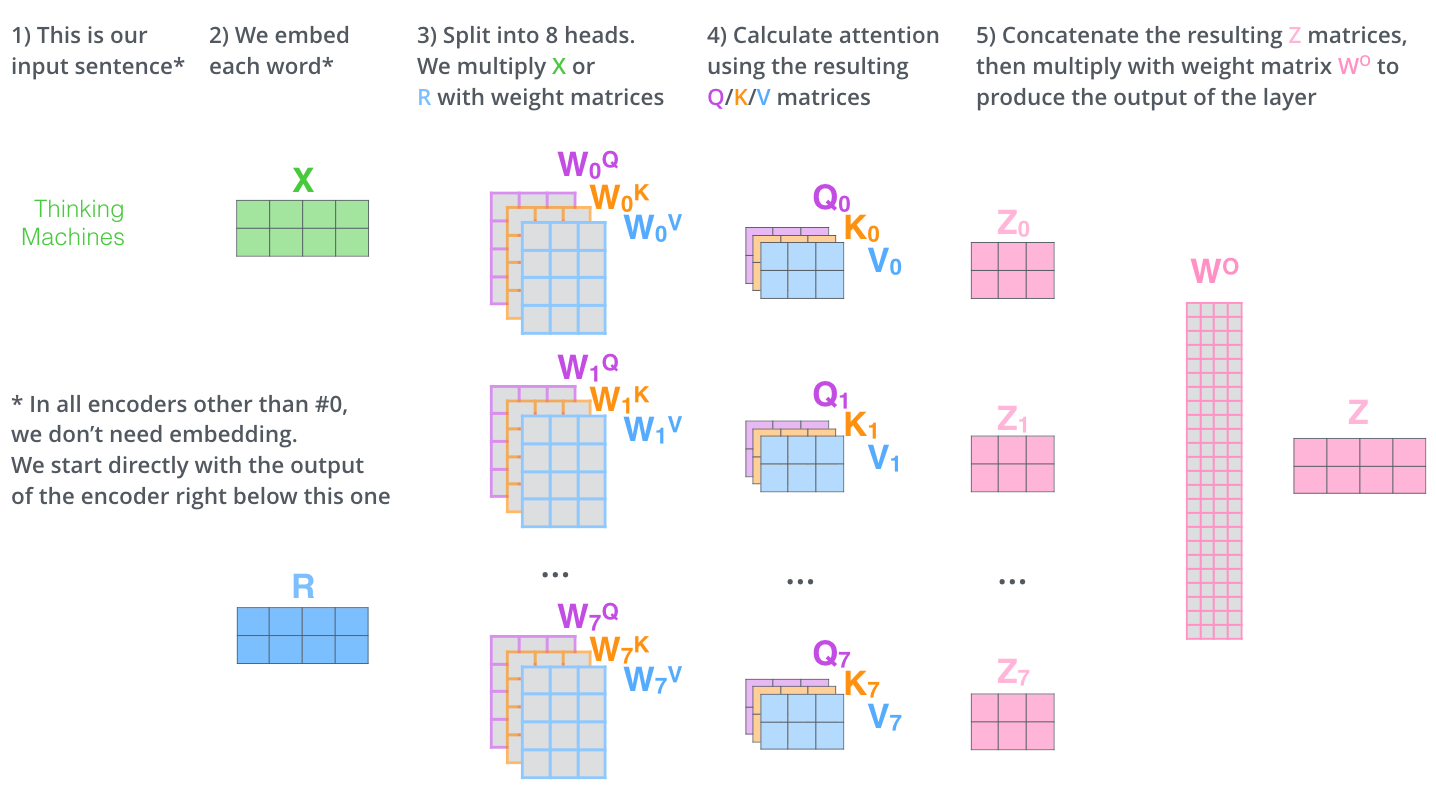
上述过程用公式可以表达如下： \[ \begin{aligned} \text { MultiHead }(Q, K, V) &\left.=\text { Concat (head }_{1}, \ldots, \text { head }_{\mathrm{h}}\right) W^{O} \\ \text { where head }_{\mathrm{i}} &=\text { Attention }\left(Q W_{i}^{Q}, K W_{i}^{K}, V W_{i}^{V}\right) \end{aligned} \] 注意参数矩阵的维数 \(W_{i}^{Q} \in \mathbb{R}^{d_{\text {model }} \times d_{k}}, W_{i}^{K} \in \mathbb{R}^{d_{\text {model }} \times d_{k}}, W_{i}^{V} \in \mathbb{R}^{d_{\text {model }} \times d_{v}}, W^{O} \in \mathbb{R}^{h d_{v} \times d_{\text {model }}}\)，注意公式中 \(QW_i^Q\) 并不是矩阵相乘。

在本研究中，我们取 \(h = 8\)，即 8 个并行的注意力层。对于每个注意力层，我们取 \(d_{k}=d_{v}=d_{\text {model }} / h=64\). 由于每个注意力层中向量的维数被均分了，所以该方法与使用单个头部的注意力相比计算成本相差并不大。

Applications of Attention in Transformer

在 Transformer 中，多头部注意力以三种不同的方式进行了应用：

编码器中的使用了自我注意力层，即三个矩阵均来源于同一个地方（上一个解码器的输出或初始输入）
在解码器的第一层中，为了保证只基于当前位置之前的信息（解码器按顺序解码），在缩放点积操作之后新增了一个 mask 操作，将所有当前位置之后的数值设为 \(-\infty\)
在解码器的第二层中，查询矩阵 Q 来自于上一个解码器的输出，而值矩阵 V 和键矩阵 K 则来自于编码器的输出

Position-wise Feed-Forward Networks

在 Transformer 中，编码器和解码器的每一层都包含了一个相同结构的全连接前馈网络，独立地应用于序列的每一个位置。该网络由两层线性连接组成，中间接了一个 ReLU 激活函数，如下式所示： \[ \operatorname{FFN}(x)=\max \left(0, x W_{1}+b_{1}\right) W_{2}+b_{2} \tag{2} \] 每一层的参数不共享。网络中输入和输出的维度均为 \(d_{\text{model}} = 512\)，中间层额维度为 \(d_{ff} = 2048\).

Embeddings and Softmax

在 Transformer 中，编码器输入与解码器输入（即最终输出）使用的词嵌入来源于同一权重矩阵，且该矩阵会随着训练不断迭代更新。最终输出 softmax 层前的线性转换层也使用了该矩阵。在 Embedding 层中，我们将权重乘上了 \(\sqrt{d_\text{model}}\).

Positional Encoding

为了让模型中序列的特征能够体现，我们需要将序列的位置信息编码到输入中。将位置编码和嵌入编码相加（保证维数相同），即可得到最终的输入向量。总的来说，编码位置信息有两种方式：一种是基于公式的编码，另一种是通过训练动态学习的编码。原文作者经过测试，两种方法的效果基本相同，而基于公式的编码不需要额外训练，且能够处理训练集中未出现过的长度的序列，因此 Transformer 中使用了基于公式的位置编码： \[ \begin{array}{c}{P E_{(pos, 2 i)}=\sin (pos / 10000^{2 i / d_{\text {model}}})} \\ {P E_{(pos,2i+1)}=\cos (pos / 10000^{2 i / d_{\text {model }}})}\end{array} \] 其中 \(pos\) 表示当前 item 在序列中的位置，\(i\) 表示该 item 向量中的具体维数。

Why Self-Attention

下表给出了自我注意力机制与传统卷积神经网络或循环神经网络的对比。这里假设输入和输出序列长度均为 \(n\)，向量维数为 \(d\)。总的来看，自我注意力机制在层内复杂度、序列操作复杂度与最大路径长度上都有一定的优势。

具体来说，自我注意力机制的序列操作复杂度和最大路径长度均为 \(O(1)\)，路径长度越短，模型越容易学习到长期依赖。对于每一层的计算复杂度（时间）在序列长度小于向量维数（常见情况）时，自我注意力的优势更大。如果序列很长，可以将注意力限制在当前位置的大小为 \(r\) 的窗口内，这时相对应的最大路径长度会有所提升。

Training

下面对 Transformer 的训练策略进行简介。

Training Data and Batching

原文作者使用了两套数据集：一套是 WMT 2014 English-German dataset，包含约 4.5 million 个句子对，编码方式为 byte-pair 编码；另一套是 WMT 2014 English-French dataset，包含约 36M 个句子，编码方式为 word-piece 编码。关于具体的编码方式可以参考引文 3-4。每一个训练 batch 包含大约 25000 个句子对。

Hardware and Schedule

模型的训练环境是一个包含 8 个 NIVIDIA P1000 GPU 的计算机。原文中共训练了两种模型，一种是基于上文所描述参数的基础模型，训练时长 12 小时（每一次完整的训练约 0.4 秒）。另一种是参数量提升的 big 模型，训练时长 3.5 天，每次训练约 1 秒。关于大模型的具体参数可以参考原论文。

Optimizer

原文使用了 Adam 优化器 [5]，参数设置为 \(\beta_{1}=0.9, \beta_{2}=0.98, \epsilon=10^{-9}\)。学习率随训练过程动态变化，基于下列公式： \[ lrate=d_{\text {model }}^{-0.5} \cdot \min \left(step\_num^{-0.5}, step\_num\cdot warmup\_steps^{-1.5}\right) \tag{3} \] 学习率会先线性增大，再逐渐减小。原文中使用 \(warm\_steps =4000\).

Regularization

在训练过程中，使用了两种正则化手段：

第一种是 Residual Dropout。在每一层进行残差连接和归一化之前，先执行 dropout [6]。此外，编码器与解码器中嵌入编码与位置编码之和也应用了 dropout。对于基础模型，原文使用 \(P_{drop} = 0.1\).

第二种是 Label Smoothing。在训练过程中，使用了标签平滑策略 [7]，参数设置 \(\epsilon_{ls} = 0.1\)。这种策略会增加模型的不确定性，影响困惑度（perplexity），但会提升准确率与 BLEU 得分。

PS：以上就是论文主要内容的解读，训练章节中对于具体的方法没有展开介绍，详细内容可以查阅参考文献。论文的结果部分主要描述了模型在机器翻译任务中的表现以及不同参数设置下模型的表现，这里不作赘述，一句话概括就是比其他模型都牛批。