CS229 学习笔记之十八:机器学习的实用建议
本篇博客为 CS229 学习笔记第十八部分,主题是:强化学习中的各种算法。
调试学习算法
对于一个学习算法,有着各种各样的调试手段,不同的调试手段可以解决不同的问题,需要根据实际情况进行选择。学习算法的问题大致可以分为两类:高偏差/方差问题以及算法优化问题。
高偏差/方差问题
我们先来进一步了解方差与偏差的权衡问题。以线性回归为例,我们通过计算测试集的最小二乘误差(MSE)来评价模型的好坏: \[ \mathbb{E}_{(x,y)\sim\text{test set}}|\hat f(x)-y|^2 \]
如果 MSE 过大,一般可以从以下三个方面进行解释:
- 过拟合:模型与训练集过度相关导致难以推广至其他样本
- 欠拟合:模型没有获取训练集的足够信息导致难以捕捉输入与输出之间的联系
- 单纯噪声:测试数据中噪声过大(数据本身存在误差)
假定训练集与测试集中的数据符合同一分布: \[ y_i = f(x_i)+ \epsilon_i, \quad\text{where the noise}\;\epsilon_i\;\text{satisifies}\; \mathbb{E}(\epsilon_i)=0,\;\text{Var}(\epsilon_i)=\sigma^2 \]
对于测试集中的每个样本 \(j\),我们对于 \(y_j = f(x_j)+ \epsilon_j\) 的预测为 \(\hat{f}(x_j)\)。现在我们可以通过如下公式计算 MSE(\(\hat{f}\) 可以看做关于训练集的随机变量函数): \[ \begin{align*} \text{Test MSE}&= \mathbb{E}\left((y-\hat{f}(x))^2\right) \\ & = \mathbb{E}\left((\epsilon + f(x) -\hat{f}(x))^2\right) \\ &= \mathbb{E}(\epsilon)^2 + \mathbb{E}\left((f(x)-\hat{f}(x))^2\right) \\ &= \sigma^2 + \left(\mathbb{E}(f(x)-\hat{f}(x))\right)^2 + \text{Var}\left(f(x)-\hat{f}(x)\right) \\ &= \sigma^2 + \left(\text{Bias}\;\hat{f}(x)\right)^2 + \text{Var}\left(\hat{f}(x)\right) \end{align*} \]
推导过程利用了 \(\text{Var}(x) = \mathbb{E}(x^2) - (\mathbb{E}(x))^2\)。公式中的第一项为误差项,我们无法预测;公式中的第二项为偏差项,表示平均来看,\(\hat{f}\) 没有正确预测 \(f\) ,对应为欠拟合;公式中的第三项为方差项,表示 \(\hat{f}\) 过于接近训练集的输出导致在测试集上偏差较大,对应为过拟合。
大部分情况下,减少方差或偏差中的一项意味着增加另一项,因此我们需要考虑好两者之间的权衡。以贝叶斯逻辑回归为例,出现高偏差或高方差的可能解决措施有:
- 尝试更多的特征(解决高偏差)
- 尝试更少的特征(解决高方差)
- 使用更大的训练集(解决高方差)
算法优化问题
学习算法的另一个常见问题是算法是否收敛。对于这个问题,我们可以考虑如下方式进行调试:假定 SVM 比贝叶斯逻辑回归(BLR)更好,但是你仍然希望采用贝叶斯逻辑回归,令 \(\theta_{\text{SVM}}\) 表示 SVM 学习得到的参数,\(\theta_{\text{BLR}}\) 表示 BLR 学习得到的参数。我们使用加权准确率来评估算法的好坏: \[ a(\theta) = \max_\theta \sum_i w^{(i)} 1\{h_{\theta}(x^{(i)})=y^{(i)}\} \]
因为 SVM 的表现优于 BLR,所以 \(a(\theta_{\text{SVM}}) > a(\theta_{\text{BLR}})\)。而 BLR 尝试去最大化(即代价函数): \[ J(\theta) = \sum_{i=1}^m \log p(y^{(i)}|x^{(i)}, \theta) - \lambda ||\theta||^2 \] 我们可以比较 \(J(\theta_{\text{SVM}})\)和 \(J(\theta_{\text{BLR}})\) 的大小
- 如果 \(J(\theta_{\text{SVM}}) > J(\theta_{\text{BLR}})\),那么说明 \(\theta_{\text{BLR}}\) 并没有最大化 \(J\),问题出在算法优化上
- 如果 \(J(\theta_{\text{SVM}}) \le J(\theta_{\text{BLR}})\),那么说明 \(\theta_{\text{BLR}}\) 成功地最大化了 \(J\),但 SVM 的表现却更好,这表示问题出在目标函数上
以贝叶斯逻辑回归为例,出现算法优化问题时的可能解决措施有:
- 提高梯度下降的迭代次数(解决算法的优化)
- 尝试牛顿方法(解决算法的优化)
- 使用不同的 \(\lambda\) 的值(解决优化目标的选择)
- 尝试 SVM(解决优化目标的选择)
误差分析
对于一个学习问题来说,通常是由一条流水线组成的,如果发生了误差,我们需要找到哪一部分导致了这一误差。下面通过一个面部识别流水线来介绍误差分析的方法,如下图所示:
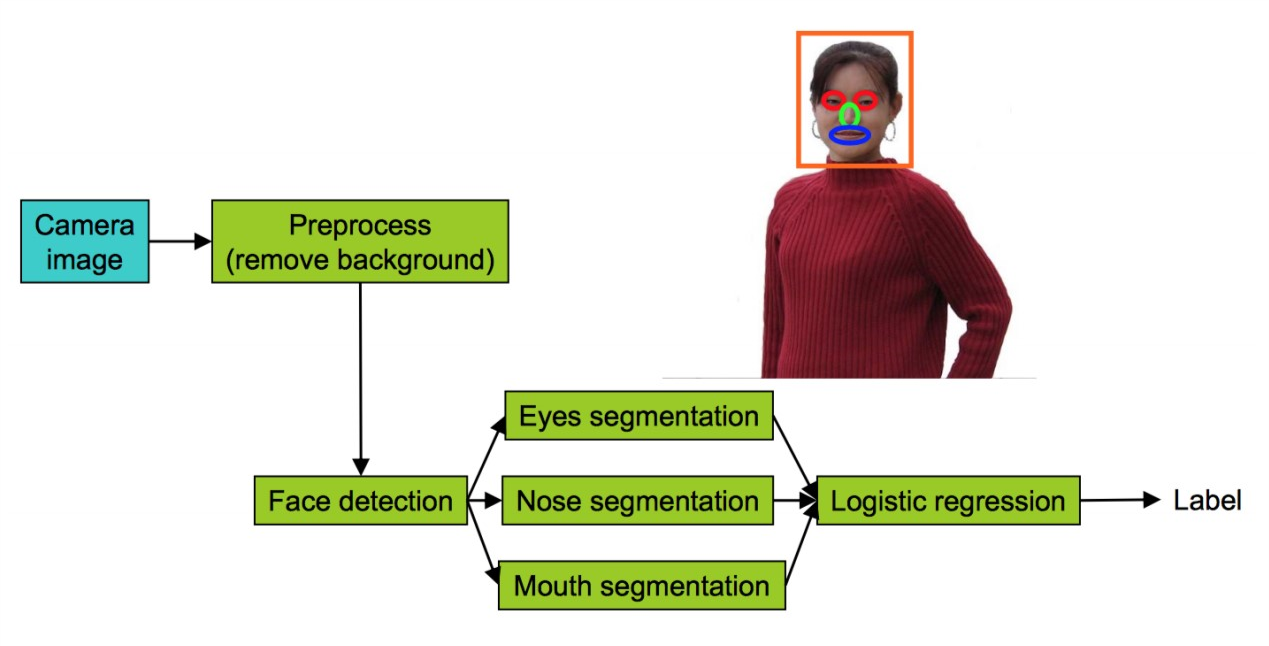
该算法可以分为如下几个步骤: 1. 从相机照片中获得输入 2. 预处理图像,去除背景 3. 检测脸部的位置 4. 检测眼睛-检测鼻子-检测嘴巴 5. 通过逻辑回归进行预测
我们可以通过将每一部分的输出替换为完美的结果,来观察哪一部分对结果的准确率贡献最大,如下表所示:
| Component | Accuracy |
|---|---|
| Overall system | 85% |
| Preprocess (remove background) | 85.1% |
| Face detection | 91% |
| Eyes segmentation | 95% |
| Nose segmentation | 96% |
| Mouth segmentation | 97% |
| Logistic regression | 100% |
可以看出,对于面部识别流水线,去除背景的影响并不是很大,而面部识别与眼睛识别对准确率的贡献最大。除了帮助改善算法,误差分析在撰写论文时也很有帮助,它可以用于解释算法的哪一部分应该被提升。
消融分析
误差分析尝试去解释算法当前的表现与完美表现的差别,而消融分析(Ablative analysis)尝试去解释一些基线表现(通常表现更差)与当前表现的差别。
以垃圾邮件分类器为例,你通过在逻辑回归中加入了以下这些有趣的特征获得了不错的结果:
- Spelling correction
- Sender host features
- Email header features
- Email text parser features
- Javascript parser
- Features from embedded images
我们可以通过消融分析了解究竟是哪些特征提升了算法性能。消融分析的方法是从最佳表现出发,逐步去除这些特征,观察算法的准确率变化,如下表所示:
| Component | Accuracy |
|---|---|
| Overall system | 99.9% |
| Spelling correction | 99.0% |
| Sender host features | 98.9% |
| Email header features | 98.9% |
| Email text parser features | 95% |
| Javascript parser | 94.5% |
| Features from embedded images | 94.0% |
在论文撰写中,消融分析可以帮助发现那些真正重要的特征(或 trick)。
分析你的错误
不要浪费时间在并不会减少你的错误率的部分,专注于真正重要的部分。以一个识别猫的图片为例,你发现数据集中有很多狗的照片,思考是不是应该构建一个专门识别狗的算法来防止误将狗识别成猫的结果出现。
你可以选取验证集中的100个错误分类的样本,看其中为狗图片的比例是多少,如果只有5%,那么即使你研究出了识别狗图片的算法,原来算法的性能也不会有多大提升。
开始一个学习问题
一般开始一个新的学习问题有两种方法:
- 仔细地设计所有步骤,然后实现。这种方法适用于研究新的算法,可能会存在过早优化的问题
- 先快速构建一个不完美的原型,然后不断地调试(大部分场景下推荐这种方法)
思维导图
