本篇博客为《剑指 offer》一书的刷题笔记(第三部分)。
面试题 7:重建二叉树
题目:输入某二叉树的前序遍历和中序遍历的结果,请重建该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。
示例
输入: 前序遍历 preorder = [3,9,20,15,7] 中序遍历 inorder = [9,3,15,20,7] 输出: 3 / \ 9 20 / \ 15 7
限制:\(0 \le 节点个数 \le 5000\)
思路及代码
二叉树的前序遍历 的顺序是:
根节点 → 左子树 → 右子树
二叉树的中序遍历 的顺序是:
左子树 → 根节点 → 右子树
其中每个子树的遍历顺序同样满足对应的前序或中序遍历顺序。对于这一题,我们可以采用递归 或者迭代 (循环)的方式来求解。递归的方法相对来说要更加简洁一些,而迭代的方法则不是非常好理解。
我们首先来看递归方法。根据前序遍历的特点,其第一个节点必然是整棵树的根节点,而对于中序遍历来说,这一根节点一般位于序列中间位置,其左边的节点位于该节点的左子树,其右边的节点则位于节点的右子树。而由于假定遍历结果中不包含重复的数字,所以我们可以根据根节点的值在中序遍历中确定其位置,从而得出左子树和右子树分别有多少个节点以及其对应的中序遍历。得到节点数量之后,我们将其代回前序遍历,即可得到左右子树对应的前序遍历。这时我们就可以通过递归再去求解这两个子树分别的左子树和右子树,直到没有节点或是只有一个节点。
上述方法的 java 实现如下:
class Solution { public TreeNode buildTree (int [] preorder, int [] inorder) { if (preorder == null || preorder.length == 0 ) { return null ; } Map<Integer, Integer> inorderMap = new HashMap <>(); int length = preorder.length; for (int i = 0 ; i < length; i++) { inorderMap.put(inorder[i], i); } TreeNode root = recur(preorder, 0 , length - 1 , inorder, 0 , length - 1 , inorderMap); return root; } private TreeNode recur (int [] preorder, int preorderStart, int preorderEnd, int [] inorder, int inorderStart, int inorderEnd, Map<Integer, Integer> inorderMap) { if (preorderStart > preorderEnd) { return null ; } int rootValue = preorder[preorderStart]; TreeNode root = new TreeNode (rootValue); if (preorderStart == preorderEnd) { return root; } else { int rootIndex = inorderMap.get(rootValue); int leftNodes = rootIndex - inorderStart; int rightNodes = inorderEnd - rootIndex; TreeNode leftSubtree = recur(preorder, preorderStart + 1 , preorderStart + leftNodes, inorder, inorderStart, rootIndex - 1 , inorderMap); TreeNode rightSubtree = recur(preorder, preorderEnd - rightNodes + 1 , preorderEnd, inorder, rootIndex + 1 , inorderEnd, inorderMap); root.left = leftSubtree; root.right = rightSubtree; return root; } } }
为了更方便地在中序遍历中找出根节点的位置,这里使用了 Map 存储中序遍历的每个元素及其对应的下标。本方法的时间复杂度 为 \(O(n)\) ,因为可能涉及深度为 \(O(n)\) 的递归(比如所有子树只有左节点),同时创建 map 也需要 \(O(n)\) 的时间;空间复杂度 也为 \(O(n)\) ,因为创建 map 和递归中创建并存储整棵树都需要 \(O(n)\) 的空间。
接下来介绍迭代方法。迭代方法的本质是利用前序遍历和中序遍历的特点,通过循环的方式重建二叉树。为了说清楚迭代的过程,下面以如下二叉树为例进行说明:
3 / \ 9 20 / / \ 8 15 7 / \ 5 10 / 4
该二叉树的前序遍历和中序遍历如下:
preorder = [3,9,8,5,4,10,20,15,7] inorder = [4,5,8,10,9,3,15,20,7]
我们观察到前序遍历的第一个元素是 3,它必是根节点,而第二个元素 9 可能位于左子树或右子树,此时再去观察中序遍历,第一个元素是 4 而不是根节点 3,说明一定存在左子树且 9 必位于左子树上(因为在前序遍历中它紧随 3 出现)。同理,我们可以判断 8、5、4 也都位于左子树,且每个节点都是上一个节点的左子节点。
当前序遍历到 4 时,其与中序遍历的第一个元素相等,这说明前序遍历已经到达了左子树的最底层,此时前序遍历的下一个元素 10 必为某个节点的右子节点(这里画图的话更容易理解)。我们需要判断 10 是哪一个节点的右子节点,观察遍历可以发现,我们将已经观察过的前序遍历的顺序反转,与中序遍历相比较,最后一次相等的节点 8 即为我们想知道的节点(从图中可以理解为找到分叉点)。
之后,我们将已经比较过的 4、5 和 8 去除,再按照上述思路比较前序遍历和中序遍历,最终可以还原出整个二叉树。
下面给出该方法的 python 实现:
class Solution : def buildTree (self, preorder: List [int ], inorder: List [int ] ) -> TreeNode: if preorder == None or not preorder: return None root = TreeNode(preorder[0 ]) cache = [root] inorder_index = 0 for i in range (1 , len (preorder)): preorder_val = preorder[i] node = cache[-1 ] if node.val != inorder[inorder_index]: node.left = TreeNode(preorder_val) cache.append(node.left) else : while cache and cache[-1 ].val == inorder[inorder_index]: node = cache.pop() inorder_index += 1 node.right = TreeNode(preorder_val) cache.append(node.right) return root
这里通过 list 实现了一个栈,用来存储已检查的前序遍历,方便反转顺序。该方法的时间复杂度 和空间复杂度 均为 \(O(n)\) 。
面试题 8 涉及指针,这里不作赘述。
面试题 9:用两个栈实现队列
题目:用两个栈实现一个队列。队列的声明如下,请实现它的两个函数 appendTail 和 deleteHead ,分别完成在队列尾部插入整数和在队列头部删除整数的功能。(若队列中没有元素,deleteHead 操作返回 -1 )
示例
输入: ["CQueue","appendTail","deleteHead","deleteHead"] [[],[3],[],[]] 输出:[null,null,3,-1]
示例中输入第一行表示操作,第二行表示对应的输入,只有插入整数时才需要提供具体的值。输出表示每一步的返回值。
限制:
\(1 <= \text{values} <= 10000\) 最多会对 appendTail、deleteHead 进行 10000 次调用
思路及代码
这道题希望我们通过两个栈来实现一个队列,栈的特点是“先进后出”,而队列的特点是“先进先出”。我们可以通过两种思路进行实现。
第一种思路是将第一个栈伪装成队列存储元素,通过第二个栈进行辅助。具体来说,我们往第一个栈中插入元素,如果栈中已有元素,则将其先全部弹出并压入到第二个栈中,再将新元素压入第一个栈,最后将第二个栈内的全部元素再弹出并压入到第一个栈中。这样第一个栈中的元素存储顺序即为栈顶为最先插入的元素(可直接弹出),而栈底为最后插入的元素。这样删除元素时直接从第一个栈弹出即可(注意要维护元素个数,队列为空时返回 -1)。
上述方法的 java 实现如下:
class CQueue { Stack<Integer> stack1; Stack<Integer> stack2; int size; public CQueue () { stack1 = new Stack <>(); stack2 = new Stack <>(); size = 0 ; } public void appendTail (int value) { while (!stack1.isEmpty()) { stack2.push(stack1.pop()); } stack1.push(value); while (!stack2.isEmpty()) { stack1.push(stack2.pop()); } size++; } public int deleteHead () { if (size == 0 ) { return -1 ; } size--; return stack1.pop(); } }
该方法的插入操作的复杂度(时间 & 空间)为 \(O(n)\) ,而删除操作的复杂度则为 \(O(1)\) 。用 LinkedList 替换 Stack 实现可以一定程度上提升速度,注意 push 方法对应为 addFirst 方法。
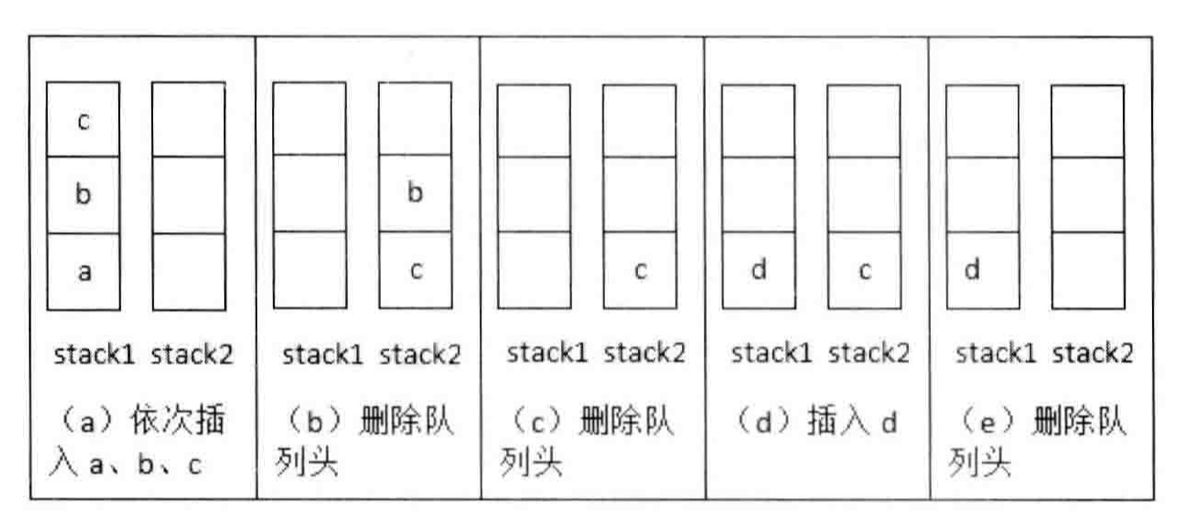
第二种思路是将两个栈一个用于插入,一个用于删除,减少来回转移的次数,如下图所示。插入元素时,直接向 stack1 中压入;删除元素时,当 stack2 为空时,我们将 stack1 中的元素逐个弹出并压入 stack2 中,再弹出 stack2 的栈顶元素;当 stack2 不为空时,直接弹出其栈顶元素即可。
上述方法的 python 实现如下:
class CQueue : def __init__ (self ): self.stack1, self.stack2 = [], [] def appendTail (self, value: int ) -> None : self.stack1.append(value) def deleteHead (self ) -> int : if self.stack2: return self.stack2.pop() if not self.stack1: return -1 while self.stack1: self.stack2.append(self.stack1.pop()) return self.stack2.pop()
该方法插入操作的复杂度为 \(O(1)\) ,而删除操作的复杂度则为 \(O(n)\) 。可以看到,两种思路一个简化了插入操作,一个简化了删除操作,妙啊。