《剑指 offer》刷题记录之四：递归和循环

本篇博客为《剑指 offer》一书的刷题笔记（第四部分）。

本篇开始将介绍与算法和数据操作相关的面试题。有很多算法都可以用递归和循环两种不同的方式实现。通常基于递归的实现方法代码会比较简洁，但性能不如基于循环的实现方法。面试时我们需要根据题目的特点和面试官的需求灵活选择。

排序和查找通常是面试时考查算法的重点。我们应该重点掌握二分查找、归并排序和快速排序，做到能够随时正确、完整地写出它们的代码。

如果面试题要求在二维数组（具体可能表现为迷宫或者棋盘）上搜索路径，那么我们可以尝试使用回溯法。通常回溯法很适合用递归的方式实现，只有面试官不允许使用递归时，我们再考虑用栈来模拟递归的过程。

如果面试题是求某个问题的最优解，并且该问题可以分为多个子问题，那么我们可以尝试用动态规划。在用自上而下的递归思路去分析动态规划问题的时候，我们会发现子问题之间存在重叠的更小的子问题。为了避免不必要的重复计算，我们用自下而上的循环代码来实现，也就是把子问题的最优解先算出来并用数组保存，接下来基于子问题的解计算大问题的解。

位运算可以看成一类特殊的算法，它是把数字表示成二进制之后对 0 和 1 的操作。位运算总共只有 5 种：与、或、异或、左移和右移。

面试题 10a：斐波那契数列

题目：写一个函数，输入 \(n\)，其斐波那契（Fibonacci）数列的第 \(n\) 项。斐波那契数列的定义如下：

\[ f(n)=\left\{\begin{array}{ll} 0 & n=0 \\ 1 & n=1 \\ f(n-1)+f(n-2) & n>1 \end{array}\right. \]

注意：答案要求取模 1e9+7（1000000007），如计算初始结果为：1000000008，请返回 1。

示例

输入：n = 2
输出：1

输入：n = 5
输出：5

限制：\(0 \le n \le 100\)

思路及代码

这道题看起来非常适合用递归方法，因为斐波那契数列的定义中即存在递归的调用。然而，这一方法存在很严重的效率问题，以 \(f(10)\) 为例，其递归求解过程可以通过下图来表示：

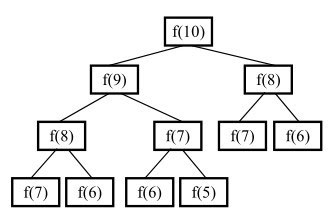
可以看到，树中存在着大量的重复节点，且随着 \(n\) 的增大而急剧增加，这会带来急剧增大的时间复杂度。为了避免重复计算，我们可以改用循环的方法，直接从下往上计算，先根据 \(f(0)\) 和 \(f(1)\) 算出 \(f(2)\)，再根据 \(f(1)\) 和 \(f(2)\) 算出 \(f(3)\)，以此类推就可以算出第 \(n\) 项了。实际上这种基于循环的思路也是动态规划思想的一种体现（将大问题拆分为小问题，并避免重复计算），与标准 dp 的区别在于只存储最近的两个变量而非整个列表。

基于上述思路的 java 实现如下：

class Solution {
    public int fib(int n) {
        int a = 0, b = 1, sum;
        for (int i = 0; i < n; i++) {
            sum = (a + b) % 1000000007; // 正数时取余和取模相同
            a = b;
            b = sum;
        }
        return a;
    }
}

该方法的时间复杂度为 \(O(n)\)，空间复杂度为 \(O(1)\)。

实际上，还有一种时间复杂度为 \(O(\log n)\) 的算法，这种算法基于如下数学公式： \[ \left[\begin{array}{lr} f(n) & f(n-1) \\ f(n-1) & f(n-2) \end{array}\right]=\left[\begin{array}{ll} 1 & 1 \\ 1 & 0 \end{array}\right]^{n-1} \] 我们可以通过数学归纳法证明上式。基于该式，我们只要求解右边的矩阵的乘方即可得到 \(f(n)\)。而乘方具有如下性质： \[ a^{n}=\left\{\begin{array}{ll} a^{n / 2} \cdot a^{n / 2} & n \text {为偶数 } \\ a^{(n-1) / 2} \cdot a^{(n-1) / 2} \cdot a & n \text {为奇数 } \end{array}\right. \] 因此我们可以基于递归实现乘方，将时间复杂度缩减为 \(O(\log n)\)。这种方法将在面试题 16 中详细讨论。

面试题 10b：青蛙跳台阶问题

题目：一只青蛙一次可以跳上 1 级台阶，也可以跳上 2 级台阶。求该青蛙跳上一个 \(n\) 级台阶总共有多少种跳法。

注意：答案要求取模 1e9+7（1000000007），如计算初始结果为：1000000008，请返回 1。

示例

输入：n = 2
输出：2

输入：n = 7
输出：21

限制：\(0 \le n \le 100\)

思路及代码

这道题目本质上还是斐波那契数列。我们可以进行如下分析：如果只有 1 级台阶，那显然只有一种跳法，如果有 2 级台阶，那么有两种跳法：一种是分两次跳，每次跳 1 级；另一种是一次跳 2 级。

对于一般的情况，我们把 \(n\) 级台阶的跳法看成 \(n\) 的函数，记为 \(f(n)\)。那么当 \(n > 2\) 时，第一次跳的时候就有两种不同的选择：一是第一次只跳 1 级，此时跳法数目等于后面剩下的 \(n-1\) 级台阶的跳法数目，即 \(f(n-1)\)；二是第一次跳 2 级，此时跳法数目等于后面剩下的 \(n-2\) 级台阶的跳法数目，即 \(f(n-2)\)。因此 \(n\) 级台阶的不同跳法的总数为： \[ f(n) = f(n-1) + f(n-2) \] 这就是一个斐波那契数列。区别在于起始数字不同： \[ f(0) = 1, f(1) = 1, f(2) = 2 \] \(f(0)\) 是基于后面两者得出的，为了保证公式的一致性。

上述思路的 python 实现如下：

class Solution:
    def numWays(self, n: int) -> int:
        a, b = 1, 1
        for _ in range(n):
            a, b = b, (a + b) % 1000000007
        return a

该方法的时间复杂度为 \(O(n)\)，空间复杂度为 \(O(1)\)。

在本问题中，如果把条件改成：一只青蛙一次可以跳上 1 级台阶，也可以跳上 2 级……也可以跳上 \(n\) 级，此时该青蛙跳上一个 \(n\) 级台阶总共有多少种跳法？我们可以用数学归纳法证明： \[ f(n) = 2^{n-1} \] 具体来说，我们先验证 \(f(1) = 1\) 成立，然后假设 \(f(n-1) = 2^{n-2}\) 成立，则按照与青蛙跳台阶类似的思路，我们有： \[ \begin{aligned} f(n) &= f(n-1) + f(n-2) + \ldots + f(1) + 1 \\ &= f(n-1) + f(n-1)\\ &= 2^{n-1} \end{aligned} \] 因此原命题成立。