《剑指 offer》刷题记录之五：查找和排序

发表于 分类于 ， 阅读次数： 本文字数： 2.3k 阅读时长 ≈ 8 分钟

本篇博客为《剑指 offer》一书的刷题笔记（第五部分）。

查找和排序都是在程序设计中经常用到的算法。常用的查找算法包括顺序查找、二分查找、哈希表查找和二叉排序树查找。本节将主要聚焦在二分查找方法，其应用场景为：

如果面试题要求在排序的数组（或者部分排序的数组）中查找一个数字或是统计某个数字出现的次数，那么我们可以尝试用二分查找算法。

哈希表和二叉排序树查找的重点在于考查对应的数据结构而不是算法。哈希表的主要优点是能够在 \(O(1)\) 时间内查找某一元素，是效率最高的查找方式，但是需要额外的空间来实现哈希表；二叉排序树查找算法对应的数据结构是二叉搜索树。我们会在之后的面试题中提到这两种方法。

排序比查找要复杂一些，常用的排序算法包括插入排序、冒泡排序、归并排序和快速排序。应聘者应该熟悉各种排序算法的特点，能够从额外空间消耗、平均时间复杂度和最差时间复杂度等方面去比较它们的优缺点。下表对这四种排序方法进行了简单总结（稳定性指原数组中相等的元素是否会保持顺序）：

排序算法 平均时间复杂度 最好情况 最坏情况 空间复杂度 排序方式 稳定性
插入排序 \(O(n^2)\) \(O(n)\) \(O(n^2)\) \(O(1)\) 原地 稳定
冒泡排序 \(O(n^2)\) \(O(n)\) \(O(n^2)\) \(O(1)\) 原地 稳定
归并排序 \(O(n \log n)\) \(O(n \log n)\) \(O(n \log n)\) \(O(n)\) 非原地 稳定
快速排序 \(O(n \log n)\) \(O(n \log n)\) \(O(n^2)\) \(O(\log n)\) 原地 不稳定

很多公司的面试官喜欢在面试环节要求应聘者写出快速排序的代码，快速排序的基本思想是：先从数组中挑选出一个元素，作为基准（一般从最左侧开始）；然后基于该基准重新排列数组，所有比基准小的元素放在基准左侧，比基准大的元素放在基准右侧。排序后，基准会被移到一个新的位置，以该位置为分界线，递归地将其左侧和右侧的子数组再按照上述方法进行排序（以子数组的左侧为新基准）。

下面给出其 java 实现（代码来源于网络）：

public class QuickSort implements IArraySort {
    @Override
    public int[] sort(int[] sourceArray) throws Exception {
        // 对 arr 进行拷贝，不改变参数内容
        int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);

        return quickSort(arr, 0, arr.length - 1);
    }

    private int[] quickSort(int[] arr, int left, int right) {
        if (left < right) {
            int partitionIndex = partition(arr, left, right);
            quickSort(arr, left, partitionIndex - 1);
            quickSort(arr, partitionIndex + 1, right);
        }
        return arr;
    }

    private int partition(int[] arr, int left, int right) {
        // 设定基准值（pivot）
        int pivot = left;
        int index = pivot + 1;
        for (int i = index; i <= right; i++) {
            if (arr[i] < arr[pivot]) {
                swap(arr, i, index);
                index++;
            }
        }
        swap(arr, pivot, index - 1);
        return index - 1;
    }

    private void swap(int[] arr, int i, int j) {
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }
}

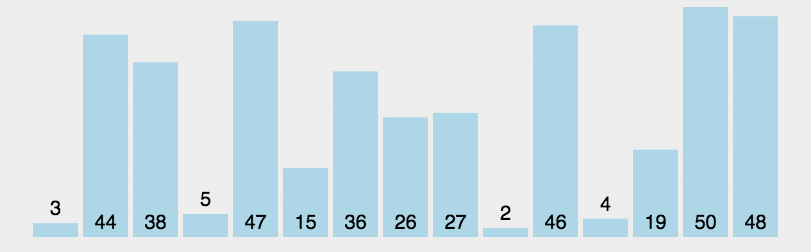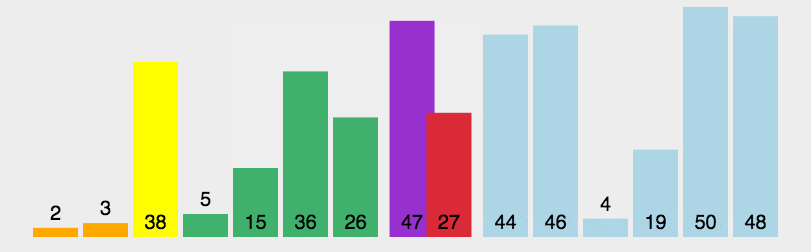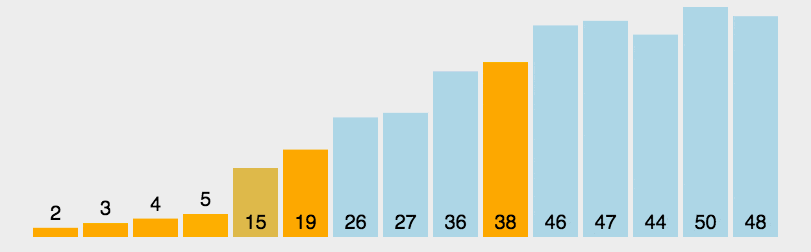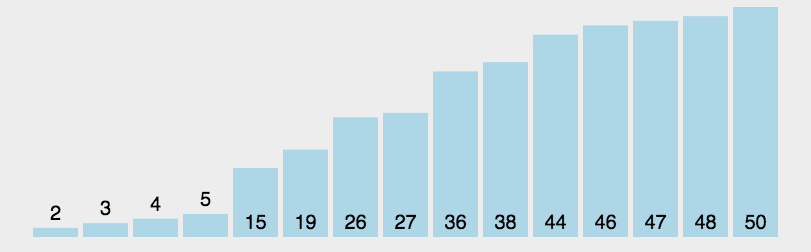
该实现对应的动图如下所示（黄色代表当前基准、橙色代表已归位基准、绿色代表比当前基准小的元素、紫色代表比当前基准大的元素、红色代表当前正在比较的元素）：

面试题 11：旋转数组的最小数字

题目：把一个数组最开始的若干个元素搬到数组的末尾，我们称之为数组的旋转。输入一个递增排序数组的一个旋转，输出旋转数组的最小元素。例如，数组 [3,4,5,1,2] 为 [1,2,3,4,5] 的一个旋转，该数组的最小值为 1。

示例

输入：[3,4,5,1,2]
输出：1

输入：[2,2,2,0,1]
输出：0

思路及代码

这道题可以采用二分查找法解决，但是由于数组中可能存在重复元素，因此需要进行分类讨论。数组的可视化如下图所示，我们将旋转点（即目标元素）左侧的数组称为左排序数组，将其右边的数组称为右排序数组。一种极端情况是左排序数组中没有元素，即未进行旋转（在本解法中并不需要单独讨论）。

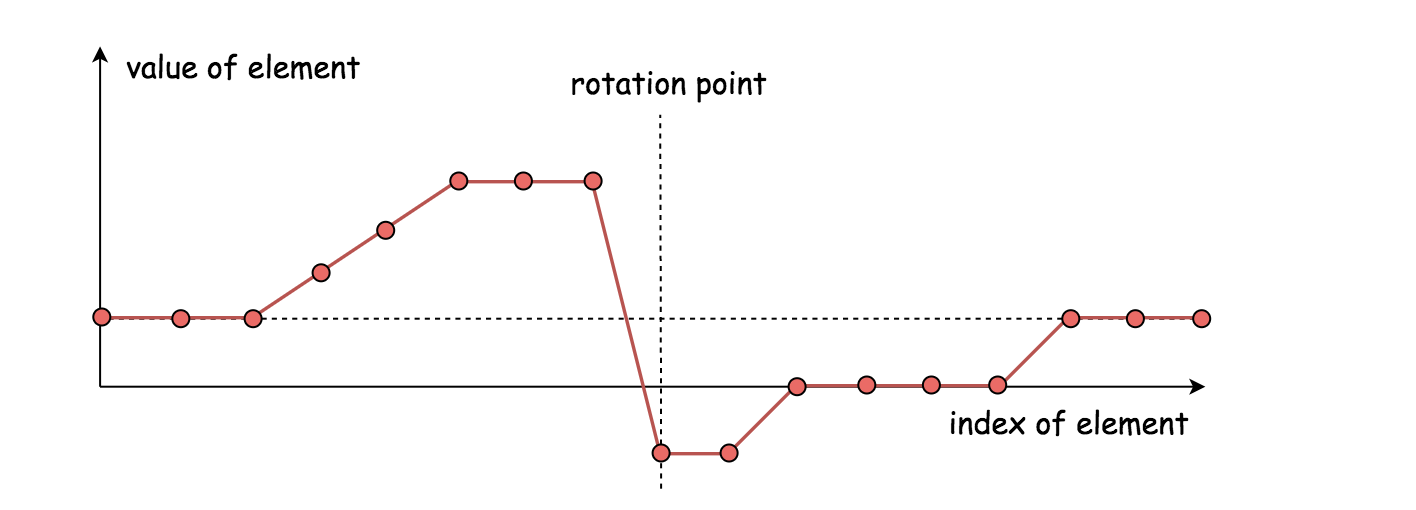
该方法的流程如下：

  • 设置两个指针 i 和 j，用来指向查找范围的左边界和右边界
  • 根据中间位置的数字 numbers[m] （m=(i+j)/2，向下取整）和右边界数字 numbers[j] 的大小关系移动指针来缩小查找范围
  • 当两个指针重合的时候即找到旋转点

对于中间位置的数字和右边界数字的大小关系，需要分三种情况讨论：

情况一：numbers[m] < numbers[j]。根据数组特点可知，中间的数字一定位于右排序数组中。此时旋转点必定位于中间位置的左侧（或就是中间位置），我们将右边界指针移到中间位置（j = m），如下图所示。注意这种情况即包含了数组未旋转的情况。

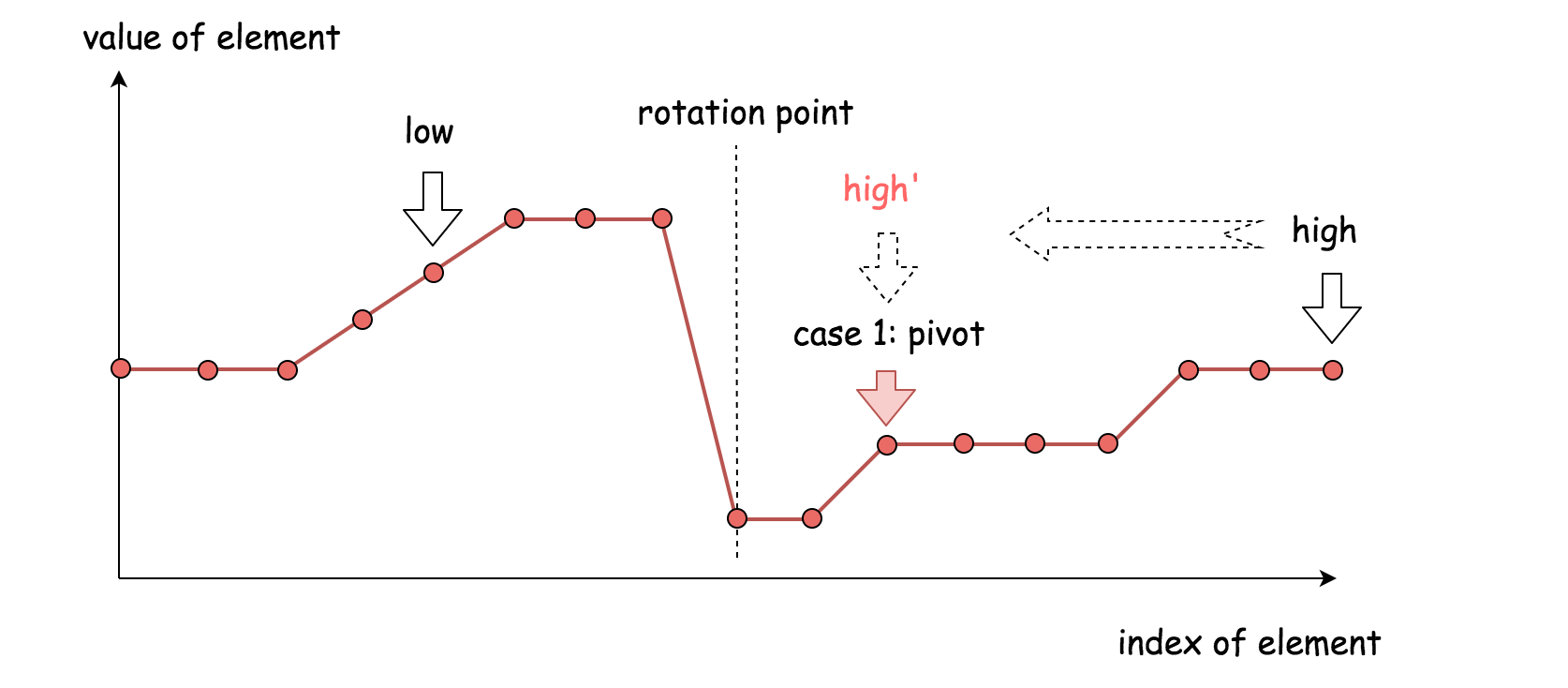
情况二：numbers[m] > numbers[j]。根据数组特点可知，中间的数字一定位于左排序数组中。此时旋转点必定位于中间位置的右侧（不包括中间位置），我们将左边界指针移到中间位置的右边（i = m + 1），如下图所示。

情况三：numbers[m] == numbers[j]。在这种情况下，我们并不能确定旋转点位于中间位置的左侧还是右侧。为了缩小查找范围，一个安全可靠的方法是将右边界指针减一（j = j - 1），如下图所示。

基于上述方法的 java 实现如下：

class Solution {
    public int minArray(int[] numbers) {
        int i = 0, j = numbers.length - 1;
        while (i < j) {
            int m = (i + j) / 2;
            if (numbers[m] > numbers[j]) i = m + 1;
            else if (numbers[m] < numbers[j]) j = m;
            else j--;
        }
        return numbers[i];
    }
}

对应的 python 实现如下：

class Solution:
    def minArray(self, numbers: List[int]) -> int:
        i, j = 0, len(numbers) - 1
        while i < j:
            m = (i + j) // 2
            if numbers[m] > numbers[j]: i = m + 1
            elif numbers[m] < numbers[j]: j = m
            else: j -= 1
        return numbers[i]

该方法的平均时间复杂度为 \(O(\log_2 N)\)，其中 \(N\) 为数组长度。在最坏的情况下（即包含相同元素时），可能需要逐个遍历元素，复杂度为 \(O(N)\)；该方法的时间复杂度为 \(O(1)\)。

关于上述方法还有两点需要讨论一下：

讨论 1：能否将中间位置的数字和左边界比较而非右边界？

不可以。因为当 numbers[m] > numbers[i] 时，由于左排序数组可能为空（即未发生旋转），所以我们无法确定中间位置的数字是在左排序数组还是右排序数组中。而由于右排序数组必定存在，所以不会出现这个问题。例如下面两个数组，上面数组的旋转点在中间位置的左侧，而下面数组的旋转点在中间位置的右侧：

numbers = [1, 2, 3, 4, 5]
numbers = [3, 4, 5, 1, 2]

讨论 2：关于右边界指针减一的可靠性证明。

当 numbers[m] == numbers[j] 时，我们选择将右边界指针减一来缩小查找范围，为了证明此操作的正确性，我们只需要证明执行操作后，旋转点 k 仍在 [i, j] 区间内即可。为了方便理解还是以上面的那张图为例来说明：

情况一：如果 m 在右排序数组中，此时数组 \([m, j]\) 内所有元素相等，执行 j = j - 1 操作后只会抛弃一个重复值，旋转点仍位于区间内；

情况二：如果 m 在左排序数组中，此时要再根据旋转点的值 numbers[k] 和右边界 numbers[j] 的大小关系分情况讨论：

若 numbers[k] < numbers[j]：即 j 左侧还有更小的元素，执行 j = j - 1 操作后旋转点仍位于区间内；

若 numbers[k] == numbers[j]：若 j > k，则执行操作后仍满足要求；若 j == k，此时执行操作后旋转点 k 可能不位于区间内，但是根据数组的特点，区间 [i,m] 内的元素一定都等于旋转点的值，最终必定返回正确的值（索引不正确），例如下面的例子：

numbers = [1, 1, 1, 2, 3, 1]
# i = 0, m = 2, j = 5

综上所述，该方法能够正确地找出旋转数组的最小数字。

PS：原书中给出的二分查找法以左边界指针的数字小于右边界为循环结束条件，对于特殊情况采取了顺序查找的方法，并不是很简洁高效，这里不做展开。