《剑指 offer》刷题记录之六：回溯法

本篇博客为《剑指 offer》一书的刷题笔记（第六部分）。

回溯法可以看成蛮力法的升级版，它从解决问题每一步的所有可能选项里系统地选择出一个可行的解决方案。回溯法非常适合由多个步骤组成的问题，并且每个步骤都有多个选项。

我们可以将用回溯法解决的问题的所有选项用树状结构表示。在某一步有 \(n\) 个可能的选项，那么该步骤可以看成是树状结构中的一个节点，每个选项看成树中的节点连接线，经过这些连接线到达该节点的 \(n\) 个子节点。树的叶节点对应着终结状态。如果在叶节点的状态满足题目的约束条件，那么我们就找到了一个可行的解决方案。

如果在叶节点的状态不满足约束条件，那么只好回溯到它的上一个节点再尝试其他的选项（对于具体的问题，可能不一定到达叶节点就回溯了）。如果上一个节点所有可能的选项都已经试过，并且不能到达满足约束条件的终结状态，则再次回溯到上一个节点。如果所有节点的所有选项都已经尝试过仍然不能到达满足约束条件的终结状态，则该问题无解。

通常回溯法适合通过递归实现，当我们到达某一个节点时，尝试所有可能的选项并在满足条件的前提下递归地抵达下一个节点。注意在递归调用之后一般需要回溯当前节点的状态，以便继续遍历下一种可能的路线（面试题 13 中不需要）。

面试题 12：矩阵中的路径

题目：请设计一个函数，用来判断在一个矩阵中是否存在一条包含某字符串所有字符的路径。路径可以从矩阵中的任意一格开始，每一步可以在矩阵中向左、右、上、下移动一格。如果一条路径经过了矩阵的某一格，那么该路径不能再次进入该格子。例如，在下面的 3×4 的矩阵中包含一条字符串 “bfce” 的路径（路径中的字母用加粗标出）。

[["a","b","c","e"], ["s","f","c","s"], ["a","d","e","e"]]

但矩阵中不包含字符串 “abfb” 的路径，因为字符串的第一个字符b占据了矩阵中的第一行第二个格子之后，路径不能再次进入这个格子。

示例

输入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
输出：true

输入：board = [["a","b"],["c","d"]], word = "abcd"
输出：false

限制：

• 1 <= board.length <= 200
• 1 <= board[i].length <= 200

思路及代码

这道题是典型的回溯法的应用，也就是深度优先搜索 + 剪枝方法。在本题中，递推的终止条件是索引越界或当前矩阵元素与目标字符不同（包括当前元素已访问）。

在具体实现时，我们通过向递归参数中传递当前目标字符串的索引 k 来帮助判断，此外，我们会在当前递归中将已访问的元素置为无关字符（保证与目标字符不等），以防止再次访问。需要注意，在当前递归完成后，需要还原已访问元素的状态，以开启下一条路线的搜索。

本方法的 java 实现如下：

class Solution {
    public boolean exist(char[][] board, String word) {
        char[] words = word.toCharArray();
        for (int i = 0; i < board.length; i++) {
            for (int j = 0; j < board[0].length; j++) {
                if (dfs(board, words, i, j, 0)) return true;
            }
        }   
        return false;
    }
    
    private boolean dfs(char[][] board, char[] word, int i, int j, int k) {
        if (i >= board.length || i < 0 || j >= board[0].length || j < 0 || board[i][j] != word[k]) return false;
        if (k == word.length - 1) return true;
        char tmp = board[i][j]; // 设置缓存变量
        board[i][j] = '/';
        boolean res = dfs(board, word, i + 1, j, k + 1) || dfs(board, word, i - 1, j, k + 1) || dfs(board, word, i, j + 1, k + 1) || dfs(board, word, i, j - 1, k + 1);
        board[i][j] = tmp; // 递归完成后回溯状态
        return res;
    }
}

对应的 python 实现如下：

class Solution:
    def exist(self, board: List[List[str]], word: str) -> bool:
        def dfs(i, j, k):
            if not 0 <= i < len(board) or not 0 <= j < len(board[0]) or board[i][j] != word[k]: return False # python 支持连续不等式
            if k == len(word) - 1: return True
            tmp, board[i][j] = board[i][j], '/'
            res = dfs(i + 1, j, k + 1) or dfs(i - 1, j, k + 1) or dfs(i, j + 1, k + 1) or dfs(i, j - 1, k + 1) # 向上下左右四个方向递归
            board[i][j] = tmp
            return res

        for i in range(len(board)):
            for j in range(len(board[0])):
                if dfs(i, j, 0): return True
        return False

关于方法的复杂度分析，我们假设 \(M\), \(N\) 分别为矩阵行列大小， \(K\) 为字符串 word 长度。则最坏情况下，需要遍历矩阵中长度为 \(K\) 的字符串的所有方案（共有三种可能的方向），时间复杂度为 \(O(3^K)\)，矩阵中共有 \(M*N\) 个起点，因此总的时间复杂度为 \(O(3^KMN)\)。关于空间复杂度，搜索过程中的递归深度不超过 \(K\)，而最坏情况下 \(K = MN\)，因此递归栈需要使用 \(O(MN)\) 的额外空间。

面试题 13：机器人的运动范围

题目：地上有一个 m 行 n 列的方格，从坐标 [0,0] 到坐标 [m-1,n-1] 。一个机器人从坐标 [0, 0] 的格子开始移动，它每次可以向左、右、上、下移动一格（不能移动到方格外），也不能进入行坐标和列坐标的数位之和大于k的格子。例如，当k为18时，机器人能够进入方格 [35, 37] ，因为 3+5+3+7=18。但它不能进入方格 [35, 38]，因为 3+5+3+8=19。请问该机器人能够到达多少个格子？

示例：

输入：m = 2, n = 3, k = 1
输出：3

输入：m = 3, n = 1, k = 0
输出：1

限制：

• 1 <= n,m <= 100
• 0 <= k <= 20

思路及代码

这一题与上一题类似，可以使用回溯法（DFS + 剪枝）来解决。不同之处在于，本题中不涉及对当前状态的撤回，只需要将满足条件的格子进行记录，防止再次访问即可。此外，虽然题中给出了四个递归方向（上下左右），但是通过对矩阵的观察，其满足条件的解必定构成等腰直角三角形，且从原点出发的话，所有可行解必定可以通过向右和向下移动访问到，下图给出了一个示例（图片来自 leetcode 题解）：

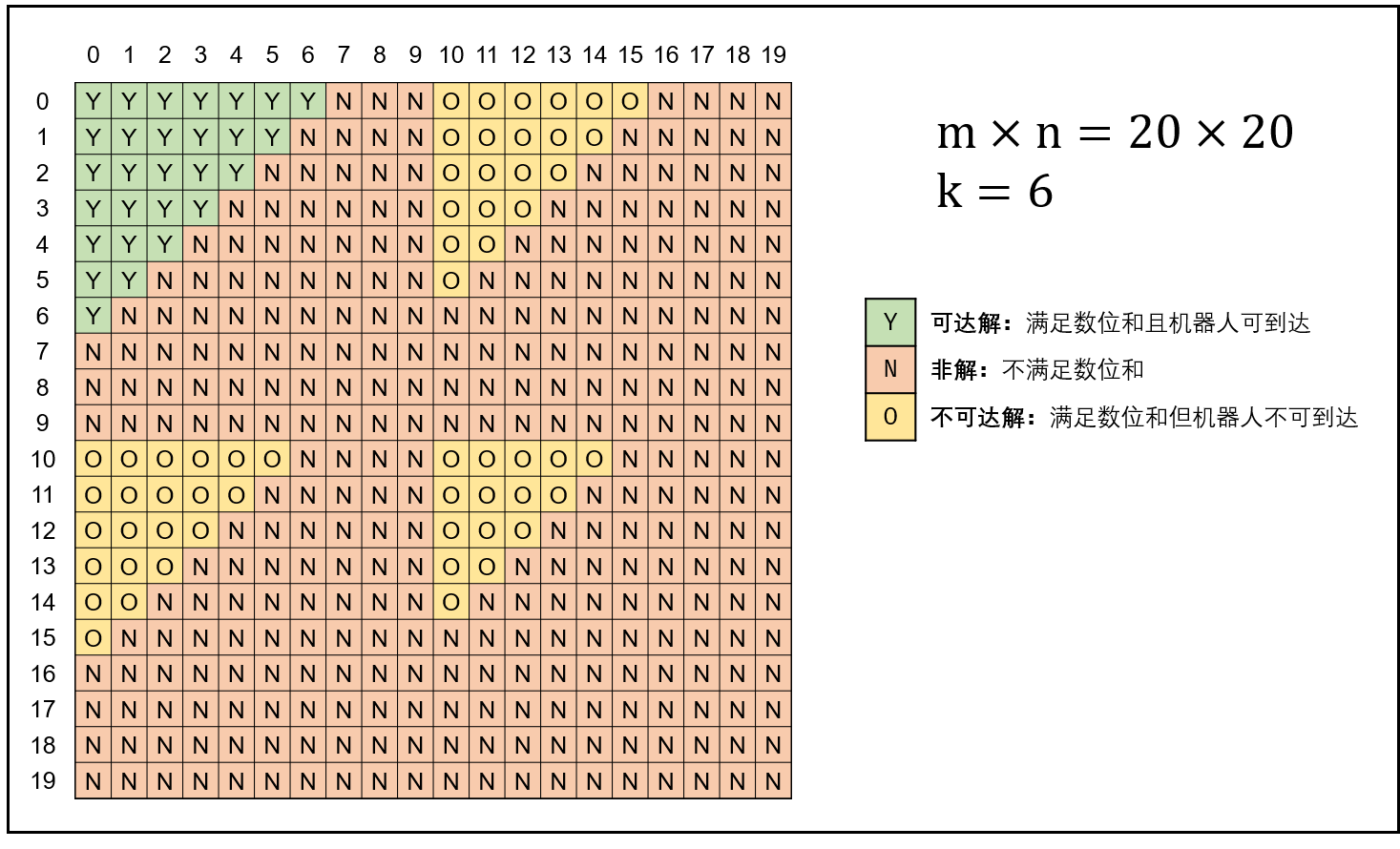
回溯法对应的 python 实现如下：

class Solution:
    def movingCount(self, m: int, n: int, k: int) -> int:
        def digit_sum(n):
            ans = 0
            while n:
                ans += n % 10
                n //= 10
            return ans
        
        def dfs(i, j):
            if i >= m or j >= n or digit_sum(i) + digit_sum(j) > k or (i, j) in visited: return 0
            visited.add((i, j))
            return 1 + dfs(i + 1, j) + dfs(i, j + 1)
        
        visited = set()
        return dfs(0, 0)

对于本题来说，由于不涉及状态的撤回，所以也可以通过广度优先搜索（BFS）来实现。一般来说，能用 DFS 解决的问题，都能用 BFS。DFS 基于栈（递归）实现，BFS 基于队列实现。由于 DFS 易于理解和编写，所以在进行矩阵的搜索问题时我们一般使用 DFS 来解决。本题由于不需要考虑遍历过节点的状态，所以 BFS 也比较简单。

基于 BFS 的 python 实现如下：

class Solution:
    def movingCount(self, m: int, n: int, k: int) -> int:
        def digit_sum(n):
            ans = 0
            while n:
                ans += n % 10
                n //= 10
            return ans
        
        queue, visited = [(0,0)], set()
        while queue:
            i, j = queue.pop(0) # 在头部 pop
            if (i < m and j < n and digit_sum(i) + digit_sum(j) <= k and (i, j) not in visited):
                visited.add((i, j))
                queue.append((i + 1, j))
                queue.append((i, j + 1))
        return len(visited)

除了上面两种方法之外，本题还可以通过简单的遍历来求解，遍历时要基于当前单元格的上方或左方的单元格的状态进行判断（保证连通性）。该方法对应的 python 实现如下：

class Solution:
    def movingCount(self, m: int, n: int, k: int) -> int:
        def digit_sum(n):
            ans = 0
            while n:
                ans += n % 10
                n //= 10
            return ans
        
        visited = set([(0,0)]) # 注意初始化要从列表转换
        for i in range(m):
            for j in range(n):
                if ((i - 1, j) in visited or (i, j - 1) in visited) and digit_sum(i) + digit_sum(j) <= k:
                    visited.add((i,j))
        return len(visited)

关于上述三种方法的复杂度分析，易知在最差情况下，上述方法都需要遍历矩阵中所有单元格，时间复杂度和空间复杂度均为 \(O(MN)\)。