《计算机图形学基础》读书笔记(一)
本篇博客为《计算机图形学基础》的第一章读书笔记。
计算机图形学(computer graphics)可以用来描述通过计算机来创造与操作图像的任何用途。本书介绍了创造与操作这些图像的基本算法与数学工具,特别是用于产生三维物体与场景合成图像的算法与工具。
在实际场景下,计算机图形学需要基于特定的硬件、文件形式以及图形学 API 展开,而本书中会尽量避免依赖特定的硬件或 API,专注于适用于大多数场景的标准术语与概念。
本章节将定义部分基本术语,提供一些计算机图形学的背景知识,以及计算机图形学相关的信息来源。
图形学领域
一般来说,计算机图形学的主要领域包括:
- 建模(Modeling):计算机可存储的关于形状与外观属性的数学规范
- 渲染(Rendering):从三维计算机模型中创建具有光影的图像(shaded images)
- 动画(Animation):通过图像的序列创造出运动的假象(基于建模与渲染完成,并添加随时间推移的动作处理)
除此之外,计算机图形学还涉及一些其他的领域,包括用户交互、虚拟现实、可视化、图像处理、三维扫描、计算摄影等。
主要应用
计算机图形学的主要应用方向包括:
- 电子游戏(Video games)
- 卡通(Cartoons)
- 视觉特效(Visual effects)
- 动画电影(Animated films)
- 计算机辅助设计/制造(CAD/CAM)
- 模拟(Simulation)
- 医学影像(Medical imaging)
- 信息可视化(Information visualization)
图形学 API
使用图形学库的关键在于处理图形学 API(graphics API)。图形学 API 是一系列执行图形学基本操作的函数集合,例如绘制物体的 3D 表面。
每个图形学程序都需要能使用两种相关的 API:
- 用于视觉输出的图形学 API
- 获取用户输入的用户界面 API
当前针对图形学与用户界面 API,有两类主要的范式:
- 集成方式(以 Java 为代表)。图形学与用户界面工具是集成在一起的可移植标准化包,作为语言的一部分
- 分离方式(以 Direct3D 和 OpenGL 为代表)。绘图命令是语言相关(例如 C++)的软件库的一部分,用户界面软件则是一个独立实体(不同系统中可能不同)
对于后一种方式来说,编写可移植的代码相对困难(对于简单的程序,可以考虑用一个可移植的软件库层来封装系统特定的用户界面代码)。
图形学管线
如今,每个桌面电脑都具有一个强大的 3D 图形学管线(graphics pipeline)。具体来说,其是一个特殊的软件/硬件子系统,能够高效地绘制出具有透视特征的 3D 基元。通常,这些基元体现为具有共同顶点的 3D 三角形(triangles),管线的基本操作即为将 3D 的顶点位置映射到 2D 的屏幕位置,并对三角形进行光影处理(渲染),使其看起来逼真并以正确的从后向前(back-to-front)的顺序出现。
在计算机图形学领域的研究中,以正确的从后向前的顺序绘制三角形曾经是一个重要的研究课题,而现在其通常使用 z-buffer (深度缓冲)来解决,该方法使用了一种特殊的内存缓冲来以暴力的方式解决这一问题。
另一方面,图形学管线中所使用的几何操作可以通过一个 4D 坐标空间完成,该空间由三个传统的几何坐标(xyz)和第四个同质(homogeneous)的坐标(用于帮助透视观察)构成。这些 4D 坐标使用 \(4\times4\) 的矩阵与 4 个向量进行操纵。图形学管线包含了大量用于高效处理与组合这些矩阵和向量的机制,该 4D 坐标系统也是计算机图形学入门必须掌握的一项内容。
图像生成的速度高度依赖于绘制的三角形数量。由于在很多应用中,交互性要比视觉质量更加重要,所以表达模型时最小化三角形的数量是非常必要的。此外,如果以较远的距离观察模型,所需要的三角形数量要少于从更近的距离观察模型,这表明通过不同的细节级别(LOD)来表示模型是很有用的。
数值问题
很多图形学程序本质上就是计算 3D 数值的代码,在这些程序中数值问题(numerical issues)至关重要。在以前,由于机器对于数字的内部表示方法各异,很难以一种鲁棒且可移植的方式处理这一问题。如今,几乎所有的现代计算机都遵循 IEEE 浮点数标准(IEEE floating-point standard),其允许程序员在如何处理某些数值条件时作出方便的假设。
IEEE 浮点数标准有着许多对于编码数值算法非常有价值的特征。首先,IEEE 浮点数标准对于实数有三个特殊值:
- 正无穷(\(\infty\)):一个比其他所有有效数字(valid number)都大的有效数字。
- 负无穷(\(-\infty\)):一个比其他所有有效数字都小的有效数字。
- 非数字(NaN):未定义结果的操作所产生的无效数字,例如 0 除 0。
基于上述特殊值,IEEE 制定了一些特殊运算规则: \[ \begin{aligned} &+a /(+\infty)=+0 \\ &-a /(+\infty)=-0 \\ &+a /(-\infty)=-0 \\ &-a /(-\infty)=+0 \end{aligned} \] 其中 \(+0\) 和 \(-0\) 只在部分场景下存在差异。除了上述特殊规则外,还有一些符合预期的操作,具体如下: \[ \begin{aligned} \infty+\infty &=+\infty \\ \infty-\infty &=\mathrm{NaN} \\ \infty \times \infty &=\infty \\ \infty / \infty &=\mathrm{NaN} \\ \infty / a &=\infty \\ \infty / 0 &=\infty \\ 0 / 0 &=\mathrm{NaN} \end{aligned} \] 关于特殊值的布尔表达式包括:
- 所有有限合法数字都小于 \(+\infty\)
- 所有有限合法数字都大于 \(-\infty\)
- \(-\infty\) 小于 \(+\infty\)
关于 NaN 的表达式还具有如下规则:
- 任何包含 NaN 的算术表达式的结果都是 NaN
- 任何包含 NaN 的布尔表达式的结果都是 false
除了以上规则之外,IEEE 浮点数标准对于除 0 操作的处理也非常有用,其规定:对于任意正实数 \(a\)(可以再添加符号),下述除 0 规则成立(注意是针对 \(+0\)): \[ \begin{aligned} &+a /+0=+\infty \\ &-a /+0=-\infty \end{aligned} \] 基于 IEEE 规则,很多数值计算可以变得更加简单。举例来说,对于下面的表达式: \[ a=\frac{1}{\frac{1}{b}+\frac{1}{c}} \] 这种表达式常在电阻或透镜计算中出现,如果除 0 导致了程序异常(在 IEEE 标准前常出现),则需要额外设置两个 if 表达式来检查 b 或 c 的值。而在 IEEE 标准化,如果 b 或 c 是0,我们会计算得到 a 的值为 0,无需添加判断条件。
另一种常用的避免特殊检查的技巧是利用 NaN 的布尔属性,例如如下代码片段: \[ \begin{aligned} &a=f(x) \\ &\text { if }(a>0) \text { then } \\ &\text { do something } \end{aligned} \] 这里函数 \(f\) 可能会返回一些特殊值,例如 NaN,但是 if 表达式可以正常执行,从而保证最终返回结果的正确性。总的来看,IEEE 标准可以让程序更加简洁、健壮与高效。
效率
提升代码的效率并没有捷径可走,需要基于不同的架构进行仔细的权衡(tradeoff)。针对当前的计算机发展趋势,程序员应该更加关注内存访问的模式而非操作数,因为内存速度的发展并没有跟上处理器的速度。
下面给出一种合理的提升代码效率的方式(需要按照顺序执行,可以跳过不需要的步骤):
- 以最直接的方式编写代码。根据需要动态计算中间结果,而不是存储它们
- 以优化模式进行编译
- 使用任意分析工具来发现当前代码的关键瓶颈
- 检查数据结构以寻找提升本地性的方法(例如让数据单元大小匹配目标架构上的缓存/页面大小)
- 如果分析工具显示瓶颈在于数值计算,可以检查编译器生成的汇编代码,尝试重写源代码来提升效率
设计与编码图形学程序
在图形学编程中,有一些常见的通用策略,本小节将对这些策略进行简要的介绍。
类设计
图形学程序的一大关键在于为几何实体(例如向量与矩阵)以及图形学实体(例如 RGB 颜色和图像)提供良好的类或例程(routines)。这些类或例程应该尽可能的简洁与高效。下面列举了一些基本的类:
- vector2。一个包含 x 与 y 组分的 2D 向量类,应该以数组形式存储,并支持向量相关的运算操作
- vector3。一个类似于 vector2 的 3D 向量类
- hvector:一个包含 4 个组分的同质性向量
- rgb:一个存储了 3 个组分的 RGB 颜色类,需要支持 RGB 相关的运算操作
- transform:一个用于变换的 \(4\times4\) 矩阵,应该包含矩阵相乘以及应用于位置(与位移存在差异,这里不做区分)、方向与平面法线向量(surface normal vector)的成员函数
- image:一个包含输出操作的 RGB 像素的二维数组
单精度 vs 双精度
如之前所述,现代计算机架构建议减少内存使用并保持一致的内存访问能够提升代码的效率。使用单精度浮点数(float)可以较好地遵循这一建议。然而,为了避免数值问题,建议使用双精度(double)的运算。在实际编写程序时,需要进行权衡,最好在类定义时提供默认设定(例如几何运算使用 double,颜色计算使用 float)。
调试图形学程序
对于图形学程序来说,有时候传统的调试工具针对复杂程序会比较不便,同时可能难以发现一些概念性的问题,导致了大量的时间浪费。下面介绍一些图形学中比较有用的调试策略。
科学方法
科学方法要求我们直接创建出目标图像,观察其存在的问题,然后提出问题产生原因的假设并进行测试,通过不断的试验最终定位问题并进行解决。与传统的调试方法不同,科学方法不要求我们立即定位到错误值或者发现概念上的错误,而是通过观察→假设→试验验证的类似科学研究的方式来进行调试(文中以光线追踪程序中常出现的阴影瑕疵问题为例进行了进一步说明)。
将图像作为调试输出
在很多情况下,图形学程序中最简单的获取调试信息的方式是输出的图像本身。如果我们想知道运算中某些变量的值,我们可以修改程序直接将这些值复制到输出图像中,通过不同颜色等方式进行直观的展示。
使用调试工具
有时候,科学方法可能会产生矛盾,或是难以找到直观的方式来观察问题所在,这时我们需要使用传统的调试工具。然而,图形学程序中包含了对相同代码的多次重复执行(例如针对每个像素、每个三角形),所以从零开始逐行调试是不切实际的,且最困难的bug通常发生在复杂的输入时。
一种有效的方法是为 bug 设置一个“陷阱”。首先,确保程序是确定性的(所有的随机数都基于固定的种子生成),然后,找到有问题的像素或三角形,在怀疑有问题的代码前添加一条语句,仅针对怀疑的情况执行。例如,如果发现像素 \((126,247)\) 有问题,可以添加如下语句: \[ \begin{aligned} \textbf{if } &x=126 \text{ and } y=247 \textbf{ then} \\ &\text{print “blarg!” } \end{aligned} \] 如果在打印语句处设置断点,我们可以直接跳转到该处,通过断言与重编译等方式进行调试。这些断言应该留在程序中,以防止未来可能出现类似的错误。此外,有些调试工具还支持条件断点功能,可以不用修改代码实现上述效果。
数据可视化
由于图形学程序常常在出错前包含大量的计算中间结果,有时很难理解程序的运行方式。一种可行的方法是参考策略大量数据的科学实验,通过较为直观的图表对数据可视化(例如在光线追踪器中可视化光线树,以了解哪条路径对像素有所贡献)来帮助进行调试,同时也有利于对代码进行优化。
信息来源
书中列举了一些计算机图形学的相关会议:
- ACM SIGGRAPH
- SIGGRAPH Asia
- Graphics Interface
- the Game Developers Conference (GDC)
- Eurographics
- Pacific Graphics
- High Performance Graphics
- the Eurographics Symposium on Rendering
- IEEE VisWeek
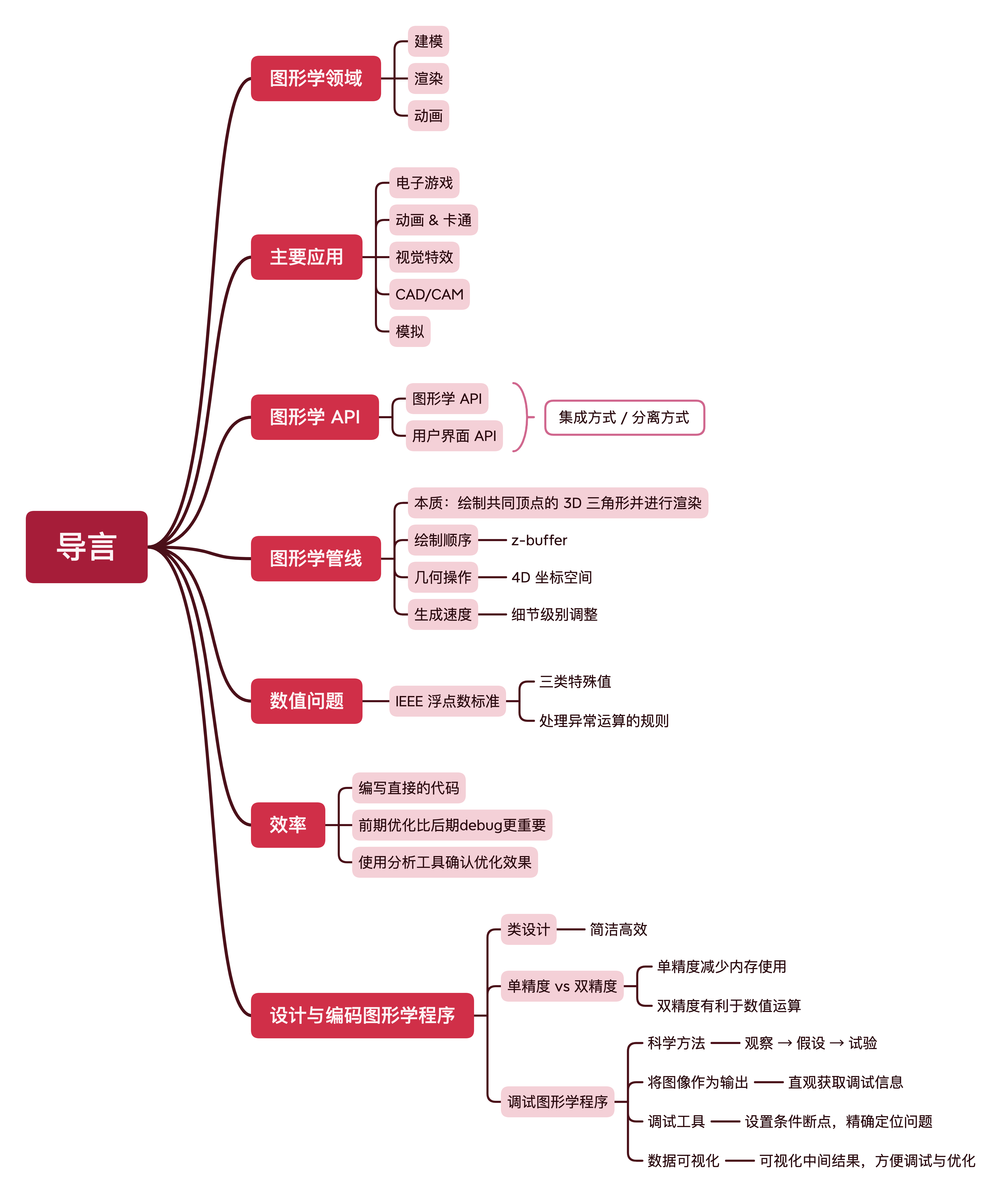
思维导图