卡特兰数入门
本篇博客主要介绍编程问题中常考的一种数列:卡特兰数。
简介
卡特兰数是组合数学中一个常在各种计数问题中出现的数列,其对应的序列为:
其通项公式为: \[ H_{n}=C_{2 n}^{n} - C_{2 n}^{n + 1} = \frac{C_{2 n}^{n}}{n+1}\left(n \geq 2, n \in \mathbf{N}_{+} \right) \] 我们可以基于通项公式得出如下递推关系: \[ \begin{aligned} H_{n+1}&=\frac{H_{n}(4 n+2)}{n+2} \\ H_{n}&=\left\{\begin{array}{ll} \sum_{i=1}^{n} H_{i-1} H_{n-i} & n \geq 2, n \in \mathbf{N}_{+} \\ 1 & n=0,1 \end{array}\right. \end{aligned} \] 下面我们将通过一些经典的题目介绍卡特兰数的基本原理,应用场景及其变式。
基本原理
我们可以通过括号匹配这个问题来了解卡特兰数的基本原理。该题目的描述如下:
对于 n 对括号,其共有多少种合法的匹配方式?
括号的合法匹配方式为:一个左括号对应一个右括号,且左括号必须要在右括号前面出现。为了方便说明,这里将左括号记作 +1,右括号记作 -1,则一个合法序列和一个非法序列可以表示为如下形式:
()(()) -> +1 -1 +1 +1 -1 -1 |
我们可以证明,对于合法序列来说,其所有前缀和必然大于等于 0,而对于非法序列来说,其必然存在前缀和小于 0 的情况。下面我们将尝试去推导序列长度为 2n 时非法序列的数量。
对于一个非法序列,我们找到其第一个和小于 0 的前缀,并对其中每一位进行取反。以上面的非法序列为例,我们会得到:-1 +1 +1 +1 -1 +1,此时该序列中共有 3+1 个 +1 和 3-1 个 -1。直观上来看,第一个小于 0 的前缀和必为 -1,即 -1 比 +1 多一个,取反后则 -1 比 + 1 少一个,这样总数上看 +1 必变为 n+1 个,-1 则变为 n-1 个(因为原来二者相等)。我们可以将该结论推广为(严格的证明省略):
对于
n对括号的每种非法匹配序列 A,都会有一个含有n+1个 +1 和n-1个 -1 的序列 B 与其一一对应。
B 的数量我们可以通过 \(C_{2n}^{n+1}\) 来计算(等价于 \(C_{2 n}^{n-1}\)),即非法序列的数量为 \(C_{2n}^{n+1}\)。而序列的总数量为 \(C_{2n}^{n}\)(从 2n 个位置中选择 n 个位置放左括号,无先后顺序),因此合法的匹配序列数量为: \[ C_{2 n}^{n}-C_{2 n}^{n+1}=\frac{C_{2 n}^{n}}{n+1} \] 此即为卡特兰数的通项公式。
应用场景
卡特兰数可以应用于很多有趣的组合数学问题,如:
给定
n个数的入栈顺序,求其有多少种出栈序列?
将进栈看做 +1,出栈看做 -1,则其为一个标准的卡特兰数,对应的结果为 \(H_n = \frac{C_{2 n}^{n}}{n+1}\)。
对于有
n+1个叶子节点,其能构成多少种形状不同的满二叉树?
这里的满二叉树使用国际定义,即如果一棵二叉树的节点要么是叶子节点,要么有两个子节点,则其为满二叉树。
我们可以证明,包含 n+1 个叶子节点(总节点个数为 2n+1)需要进行 2n 次扩展来形成满二叉树,如下图所示(月牙形表示叶子节点)。扩展即从父节点向左或向右添加子节点的过程,我们可以将其理解为左右括号匹配问题,则总共可以构成 \(H_n = \frac{C_{2 n}^{n}}{n+1}\) 种形状不同的满二叉树。

此外,上图还可以看做 n 个节点组成不同二叉树的方案数,其中圆形表示节点,月牙形表示什么都没有。我们可以基于卡特兰数的递推关系得出该方案数即为 \(H_n\),具体请参考 Leetcode 第 96 题。
在一个
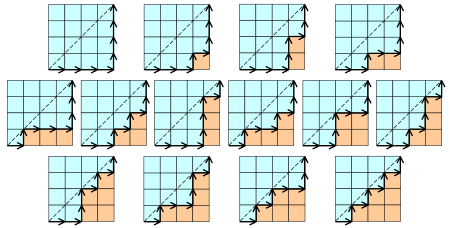
n*n的方格中从左下角走到右上角,不穿过对角线的单调路线有多少种?
通过下图我们可以发现,只存在向右走和向上走两种选择,两者的总数需匹配且任意时刻向上走的数量不能多于向右走。很明显这也是一个卡特兰数,对应的单调路线有 \(H_n\) 种。
将
n边的凸多边形以不相交的对角线分成n-2个三角形,共有多少种方法?
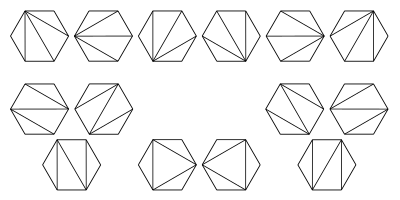
这个问题我们需要从递归的角度来考虑。因为凸 \(n\) 边形的任意一条边必定属于某一个三角形,所以我们以某一条边为基准,将这条边的两个顶点分别记作 \(P_1\) 和 \(P_{n}\),将该凸多边形的顶点依序标记为 \(P_1,P_2,\ldots,P_{n}\),再在该凸多边形中选择任意一个不属于这两个顶点的顶点 \(P_k\)(\(2 \le k \le n-1\)),来构成一个三角形,用这个三角形把该凸多边形划分为两个凸多边形,其中一个凸多边形为由 \(P_{1}, P_{2}, \ldots, P_{k}\) 构成的凸 \(k\) 边形,另一个则是由 \(P_{k}, P_{k+1}, \ldots, P_{n}\) 构成的凸 \(n-k+1\) 边形。根据乘法原理,问题的解 \(f(n)\) 等价于凸 \(k\) 边形的划分方案数乘以凸 \(n-k+1\) 边形的划分方案数,遍历所有的 \(k\),可以得到: \[ f(n)=\left\{\begin{array}{ll} \sum_{k=2}^{n-1} f(k)f(n-k+1) & n \geq 4, n \in \mathbf{N}_{+} \\ 1 & n=2,3 \end{array}\right. \] 可以看到,对于一个凸 \(n\) 边形来说,其分割方法数即等价于 \(H_{n-2}\)。下图给出了一个正六边形的分割方案,共有 \(H_4 = 14\) 种。
在实际编程中,这类问题通常可以通过找出递归关系,然后基于动态规划的方式求解。如果可以直接分辨出其为卡特兰数,那么使公式进行求解是一种最快的方法。
变式
下面介绍一种卡特兰数的变式,也是编程面试中常考的一种问题:买票问题。
假设一张门票 5 元,售票房没有额外的零钱。现在有
m个人持有 5 元的纸币,n个人持有 10 元的纸币排队买票,问有多少种排队方式,可以让每个人都买到电影票。
这道题本质上就是要让持有 5 元纸币的人和持有 10 元纸币的人保持匹配,且 5 元纸币的人需要在前面,如果将持有 5 元纸币的人看做左括号,持有 10 元纸币的人看做右括号,不难理解这就是一个卡特兰数的问题。
然而,与标准卡特兰数相比,这里的求解还有两个不同之处:首先是持有 5 元纸币的人数 m 和持有 10 元纸币的人数 n 不一定相等(注意 m 需要不少于 n ),这样我们不能直接套用卡特兰数的通项公式,而应该从原理出发重新推导,基于总序列数减去非法序列数的思想,合法序列数为 \(C_{m+n}^{m}-C_{m+n}^{m+1}\)。此外,我们还需要考虑排队的先后顺序,因此总的排队方式数为: \[
\begin{aligned}
C_{n} &=C_{m+n}^{m}-C_{m+n}^{m+1} \\
&=\frac{(m+n) !}{m ! * n !}-\frac{(m+n) !}{(m+1) ! *(n-1) !} \\
&=\frac{(m+n) !}{m ! * n !}-\frac{(m+n) ! * \frac{1}{m+1} * n}{m ! * n !} \\
&=\frac{(m+n) !}{m ! * n !} *\left(1-\frac{1}{m+1} * n\right) \\
&=\frac{(m+n) !}{m ! * n !} * \frac{m+1-n}{m+1} \\
A_n &= C_{n} * m ! * n ! \\
&= (m+n)! * \frac {m+1-n}{m+1}
\end{aligned}
\] 注:本篇文章的整体思路与部分内容参考自 LeetCode 上的一篇笔记,图片则来自 wiki 百科。
组合数计算公式如下(备忘): \[ C_n^m=\frac{A_n^m}{m !}=\frac{n !}{m !(n-m) !} \]