FLAT：基于 Flat-Lattice Transformer 的中文 NER 模型

发表于 2023-10-04 分类于人工智能，文章精读阅读次数：本文字数： 2.7k 阅读时长 ≈ 9 分钟

本篇博客是 FLAT: Chinese NER Using Flat-Lattice Transformer 一文的学习笔记。

摘要：综合利用字符与词语信息的 Lattice 结构被证明对于中文的命名实体识别具有较好的效果，然而，由于 Lattice 结构较为灵活复杂，大部分现有的基于 Lattice 的模型很难完全利用 GPU 的并行计算能力，导致推理速度较慢。本论文提出了面向中文 NER 的 FLAT（Flat-LAttice Transformer），其将 Lattice 结构转化为一个由片段（span）构成的平面（flat）结构，每个片段对应一个字符或潜在的词语，以及其在原始 Lattice 中的位置。得益于 Transformer 的能力以及精心设计的位置编码，FLAT 能够在充分利用 Lattice 信息的同时保持极佳的并行化能力。基于四个数据集的实验表明 FLAT 在模型表现与运行效率上要优于其他基于词汇的模型。

背景

命名实体识别（Named entity recognition，NER）在很多 NLP 下游任务中扮演着重要角色，与英文 NER 相比，中文 NER 往往更加困难，因为其涉及到词语的切分（分词）。Lattice 结构被证明能够更好地利用词语信息，避免分词中的错误传播。

如下图 (a) 所示，我们可以通过词表来得到一个句子中的潜在词语，形成一张有向无环图，其中每个节点表示一个字符或是一个潜在词语。Lattice 包括了一个由句子中的字符与潜在词语组成的序列，其并不完全依序排列，词语的首尾字符决定了其的位置（会与字符平行）。Lattice 中的部分词语对于 NER 来说相当重要，以下图为例，人和药店一词可以用来区分地理实体重庆与组织实体重庆人。

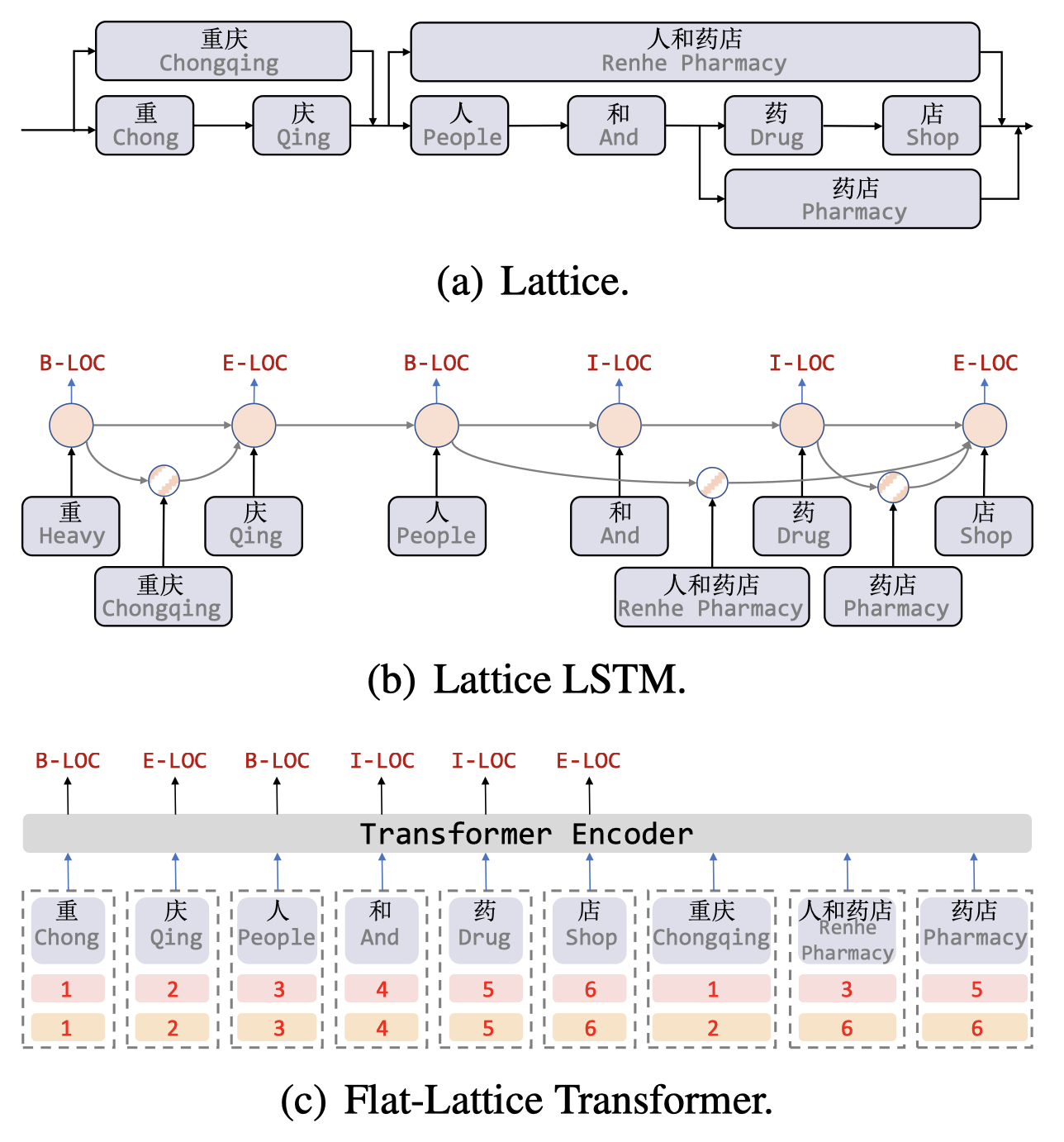
目前，利用 Lattice 结构进行 NER 的模型发展方向大致可以分为两类：

设计一个与 Lattice 输入兼容的模型，例如 lattice LSTM 与 LR-CNN。其中 lattice LSTM 利用一个额外的词语单元来编码潜在词语，并使用 attention 机制来融合每个位置的变数节点，如上图 (b) 所示；LR-CNN 则利用 CNN 来通过不同的窗口大小编码潜在词语。总的来看，RNN 和 CNN 都难以对长距离的依赖进行建模（长距离依赖对于NER 的指代等关系很有用），同时由于动态 Lattice 结构的复杂性，这些方法不能完全地利用 GPU 的并行计算能力。
将 Lattice 转化为图，使用图神经网络进行编码，例如 Lexicon-based Graph Network（LGN）与 Collaborative Graph Network（CGN）。由于图结构并不能完全消除 NER 对序列结构的依赖性，这些方法需要使用 LSTM 作为底层编码器，从而增加了模型的复杂性。

本论文针对当前相关模型的局限性，提出了面向中文 NER 的 FLAT 模型。FLAT 模型基于 Transformer 实现，能够利用全连接的 self-attention 来对序列中的长距离依赖建模。为了得到位置信息，Transformer 为序列中的每个 token 引入了位置表示（编码），类似地，在 FLAT 中针对 Lattice 结构设计了一种巧妙的位置编码，如上图 (c) 所示。具体来说，对于一个 token（字符或词语），其会包含两个位置索引：头位置与尾位置，基于这两个位置信息可以将一个 token 集合还原为 Lattice 结构，从而实现直接使用 Transformer 来建模 Lattice 输入。对于 FLAT 来说，Transformer 的自注意力机制可以使得字符直接与任意潜在词语交互，包括自包含词语，例如药的自包含词语有药店与人和药店。实验结果表明该模型在中文 NER 上的表现与推理速度要优于其他基于词汇的方法。

模型

Transformer 原理概述

本节将对 Transformer 的架构进行简要介绍。对于 NER 任务，我们只需要用到 Transformer encoder，其由自注意力层与前馈网络（FFN）两层组成，每个子层都接了残差连接与层归一化，如下图所示，其中 FFN 是一个位置独立的多层非线性感知机。

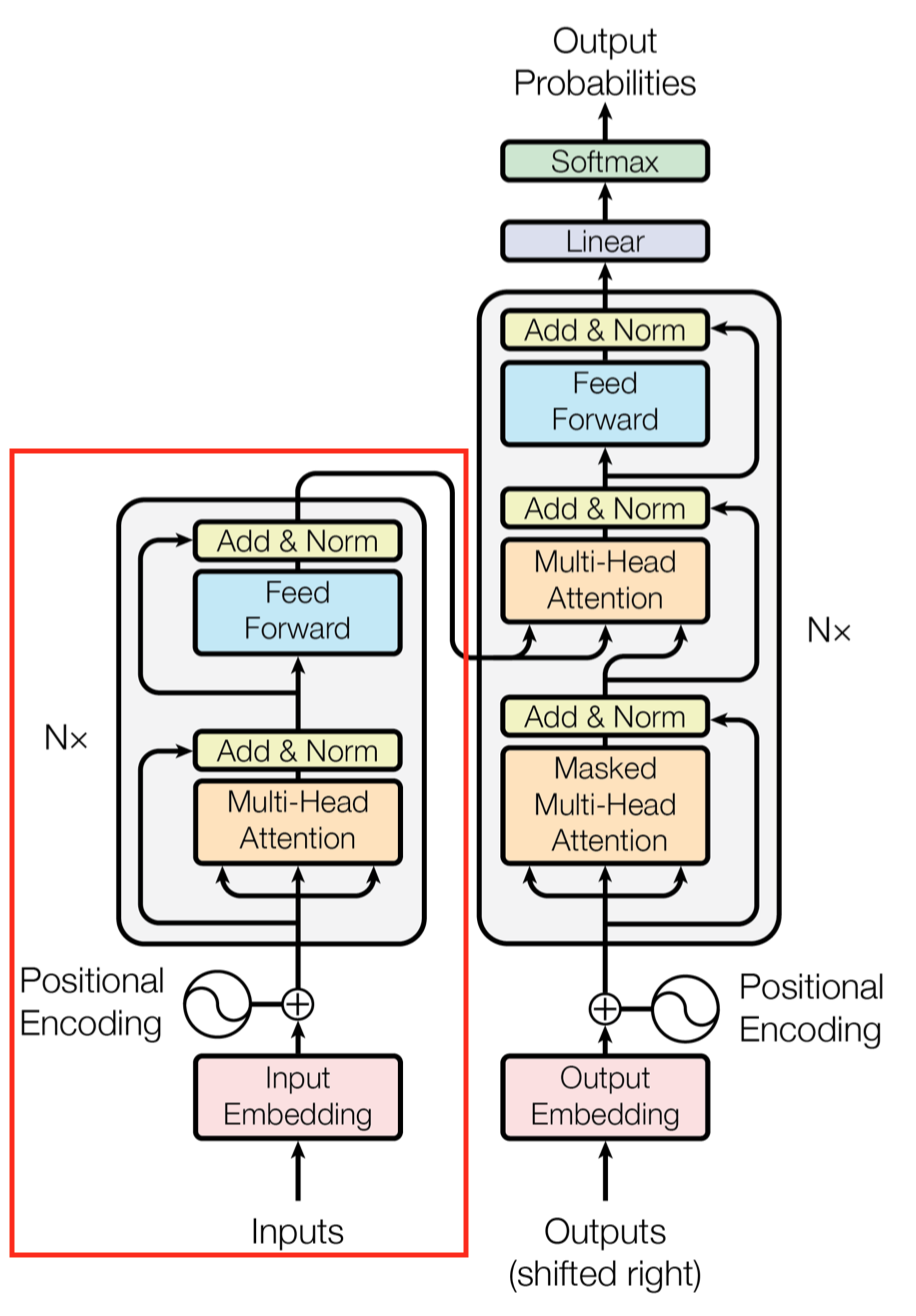
对于自注意力层，Transformer 通过独立计算多个头部的 attention 并将其结果按一定权重进行拼接以得到最终的输出，每个头部的计算公式如下： \[ \begin{align*} \operatorname{Att}(\mathbf{A}, \mathbf{V}) &=\operatorname{softmax}(\mathbf{A}) \mathbf{V} \tag{1}\\ \mathbf{A}_{\mathbf{i j}} &=\left(\frac{\mathbf{Q}_{\mathbf{i}} \mathbf{K}_{\mathbf{j}}^{\mathrm{T}}}{\sqrt{\mathrm{d}_{\text {head }}}}\right) \tag{2}\\ [\mathbf{Q}, \mathbf{K}, \mathbf{V}] &=E_{x}\left[\mathbf{W}_{q}, \mathbf{W}_{k}, \mathbf{W}_{v}\right] \tag{3} \end{align*} \] 其中 \(E\) 是 token 的嵌入（第一层）或上一层的输出，\(\mathbf{W}_{\mathrm{q}}, \mathbf{W}_{\mathrm{k}}, \mathbf{W}_{\mathrm{v}} \in \mathbb{R}^{d_{\text {model }} \times d_{\text {head }}}\) 为可学习的参数，且 \(d_{\text {head }}\) 为每个头部的维数。此外，原始 Transformer 中通过绝对位置编码来捕获序列信息，而 FLAT 中则使用了 Lattice 的相对位置进行编码。

将 Lattice 转化为平面结构

基于词汇表从字符得到一个 Lattice 结构后，我们可以将其展成平面。Flat-lattice 可以被定义为一系列片段（span）的集合，每个片段对应一个 token、一个 head 与一个 tail，其中 token 是一个字符或词语，head 与 tail 定义该 token 的首字符与尾字符的在原始序列中的位置索引。对于字符来说，head 与 tail 是相同的。

我们可以通过一个简单的算法来将 flat-lattice 恢复到原始的结构：首先选择 head 与 tail 相同的 token，恢复字符序列；然后对于其他 token 基于 head 与 tail 构建跳跃路径。由于上述转换是可恢复的，文章假定 flat-lattice 能够保持 lattice 原始结构中的所有信息。

片段的相对位置编码

Flat-lattice 结构由不同长度的片段组成，为了编码片段之间的交互，本文提出了一种编码片段相对位置的方法：对于两个片段 \(x_i\) 与 \(x_j\)，他们之间存在三种关系：相交、包含与分离，这取决与其头与尾的位置。我们将通过一个密集向量来建模这些关系，而不是直接对其进行编码，以包含片段间的更多的细节信息。具体来说，令\(\text { head }[i]\) 与\(\text { tail }[i]\) 表示片段 \(x_i\) 的头位置与尾位置，我们将通过以下四种相对距离来表明 \(x_i\) 与 \(x_j\) 之间的关系： \[ \begin{align*} &d_{i j}^{(h h)}=h e a d[i]-h e a d[j] \tag{4}\\ &d_{i j}^{(h t)}=h e a d[i]-\operatorname{tail}[j] \tag{5}\\ &d_{i j}^{(t h)}=\operatorname{tail}[i]-h e a d[j] \tag{6}\\ &d_{i j}^{(t t)}=\operatorname{tail}[i]-\operatorname{tail}[j] \tag{7} \end{align*} \] 最终的相对位置编码通过四个距离的简单非线性变化得到： \[ R_{i j}=\operatorname{ReLU}(W_{r}(\mathbf{p}_{d_{i j}^{(h h)}} \oplus \mathbf{p}_{d_{i j}^{(t h)}} \oplus \mathbf{p}_{d_{i j}^{(h t)}} \oplus \mathbf{p}_{d_{i j}^{(t t)}})) \tag{8} \] 其中 \(W_r\) 是可学习的参数，\(\oplus\) 表示连接算子（加权和），\(\mathbf{p}_{d}\) 的计算方式与原始 Transformer 相同： \[ \begin{align*} \mathbf{p}_{d}^{(2 k)} &=\sin \left(d / 10000^{2 k / d_{\text {model }}}\right) \tag{9}\\ \mathbf{p}_{d}^{(2 k+1)} &=\cos \left(d / 10000^{2 k / d_{\text {model }}}\right) \tag{10} \end{align*} \] 其中 \(d\) 表示四种距离中的一种，\(k\) 表示位置编码的维数的索引（具体的某一维，根据奇偶决定是正弦还是余弦）。自注意力的计算方式采用了原始方法的一个变种（与 transfomer-XL 和 XLNet 相同），具体公式为：

\[ \begin{align*} \mathbf{A}_{i, j}^{*} &=\mathbf{W}_{q}^{\top} \mathbf{E}_{x_{i}}^{\top} \mathbf{E}_{x_{j}} \mathbf{W}_{k, E}+\mathbf{W}_{q}^{\top} \mathbf{E}_{x_{i}}^{\top} \mathbf{R}_{i j} \mathbf{W}_{k, R} \\ &+\mathbf{u}^{\top} \mathbf{E}_{x_{j}} \mathbf{W}_{k, E}+\mathbf{v}^{\top} \mathbf{R}_{i j} \mathbf{W}_{k, R} \end{align*} \tag{11} \] 其中 \(\mathbf{W}_{q}, \mathbf{W}_{k, R}, \mathbf{W}_{k, E} \in \mathbb{R}^{d_{\text {model }} \times d_{\text {head }}}\) 和 \(\mathbf{u}, \mathbf{v} \in \mathbb{R}^{d_{\text {head }}}\) 为可学习的参数。公式 (1) 中的 \(A\) 会被 \(A^{*}\) 替代，后续的计算方式与原始 Transformer 相同。

经过 FLAT 之后，我们仅将得到的字符表征进行输出，连接到条件随机场中进行实体识别（这一部分的原理之后会通过其他文章详述）。FLAT 的整体结构如下图所示：

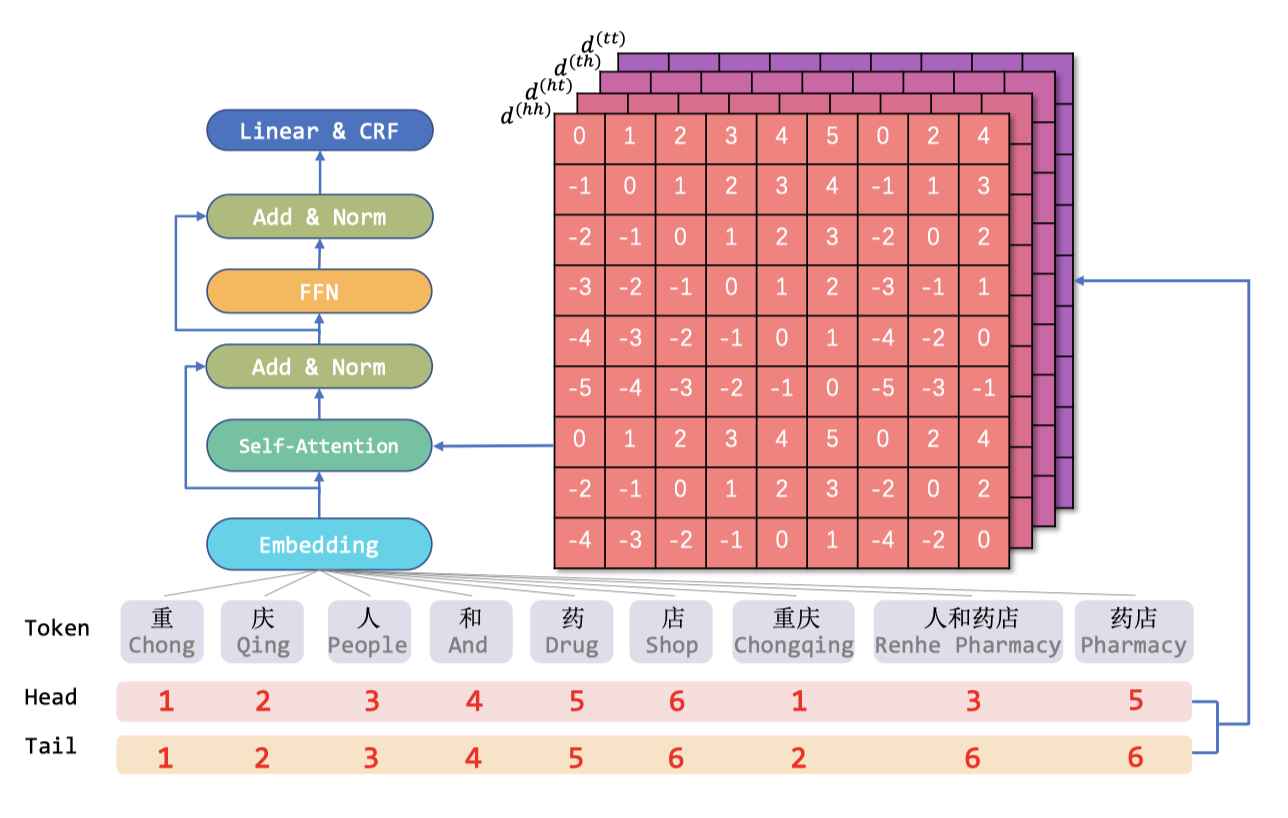
实验

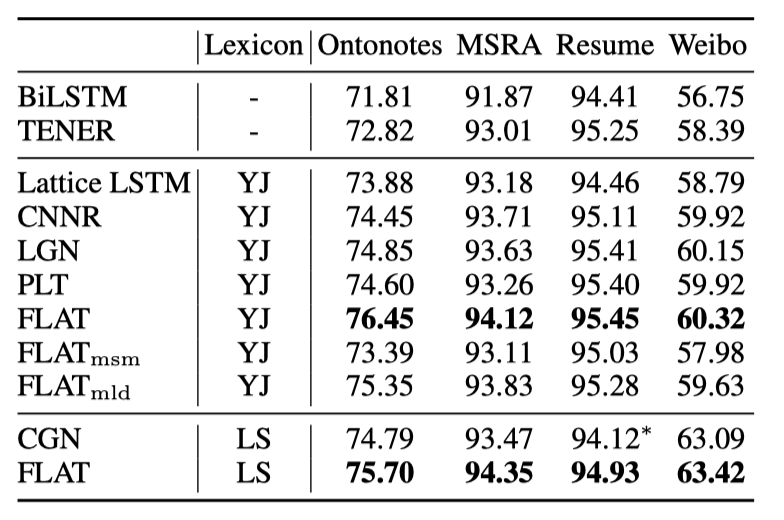
论文使用了四种中文 NER 数据集进行模型评估，基线模型选用 BiLSTM-CRF 与 TENER，并针对不同的对比使用了不同的词汇表。总体跑分（平均 F1 score）结果如下所示，总的来看，不被 mask 的完整 FLAT 模型在所有数据集上均取得了最佳表现。

进一步地，为了检验 FLAT 的两大优势：字符与自包含词语的直接交互以及对长距离依赖的建模，论文分别对自包含词语与字符之间以及长距离词语之间的 attention 进行遮罩后进行了测试，结果表明自包含词语相较于长距离依赖带来了更大的性能下降。

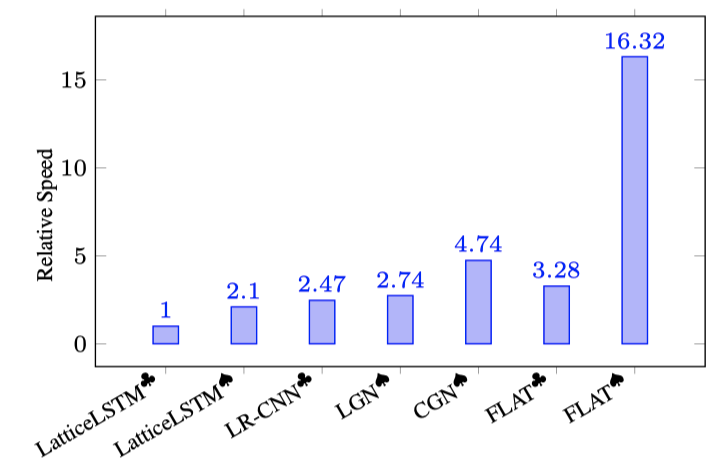
在计算效能方面，不同模型在 Ontonotes 数据集上的推理速度结果比较如下图所示，由于 FLAT 的简洁性，其可以更有效的进行并行计算，大幅提升推理速度。

此外，论文还评估了 FLAT 相比 TENER 在 NER 上的具体性能提升，以及 FLAT 与 BERT 的兼容性，具体结果可以参考原文。

总结

本文提出了一种包含词汇信息的 Flat-lattice Transformer 模型，用于中文 NER 任务。模型的核心是将 Lattice 结构转化为一系列片段的集合，并融入可训练的相对位置编码。试验结果表明模型在预测性能与推理速度上都要优于其他基于词汇的模型。

PS：在相关工作中，作者提到了一篇将 Lattice 与 Transformer 结合的类似文章：Porous Lattice Transformer，并指出 FLAT 与该模型的主要区别在于对位置信息的表示差异。