本篇博客对常用因果推断框架 DoWhy 进行了系统总结。
概述
因果推断 (causal inference)是基于观察数据进行反事实估计,分析干预与结果之间的因果关系的一门科学。虽然在因果推断领域已经有许多的框架与方法,但大部分方法缺乏稳定的实现。DoWhy 是微软发布的一个用于进行端到端因果推断的 Python 库,其特点在于:
提供了一种原则性的方法将给定的问题转化为一张因果图,保证所有假设的明确性
提供了一种面向多种常用因果推断方法的统一接口,并结合了两种主要的因果推断框架
自动化测试假设的正确性及估计的鲁棒性
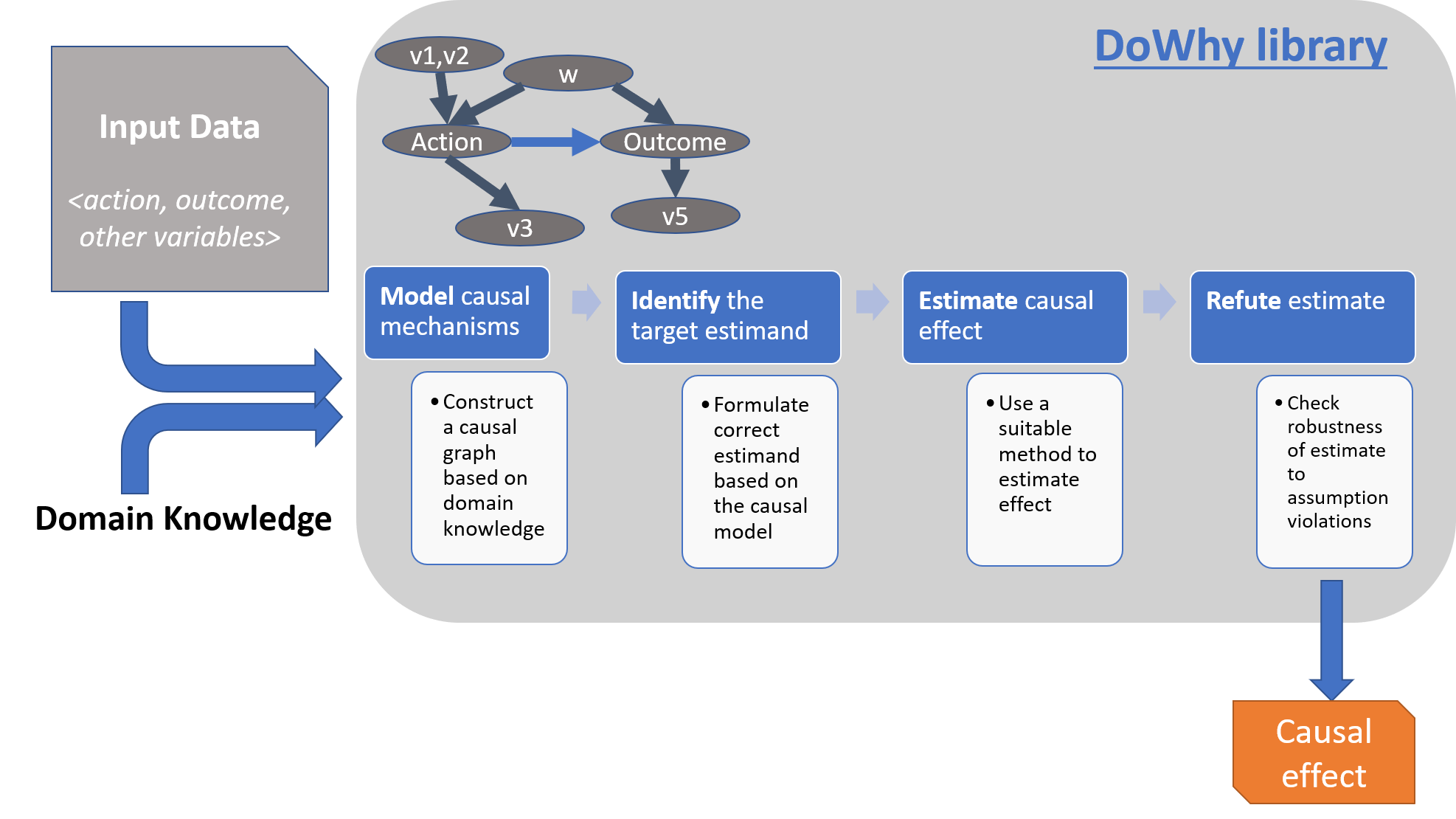
如上所述,DoWhy 基于因果推断的两大框架构建:图模型 与潜在结果模型 。具体来说,其使用基于图的准则与 do-积分来对假设进行建模并识别出非参数化的因果效应;而在估计阶段则主要基于潜在结果框架中的方法进行估计。DoWhy 的整个因果推断过程可以划分为四大步骤:
建模 (model):利用假设(先验知识)对因果推断问题建模识别 (identify):在假设(模型)下识别因果效应的表达式(因果估计量)估计 (estimate):使用统计方法对表达式进行估计反驳 (refute):使用各种鲁棒性检查来验证估计的正确性
下图总结了 DoWhy 的整体流程:
下面将分别对这四个步骤及其所涉及的方法进行简要介绍。
建模
DoWhy 会为每个问题创建一个因果图模型,以保证因果假设的明确性。该因果图不需要是完整的,你可以只提供部分图,来表示某些变量的先验知识(即指定其类型),DoWhy 支持自动将剩余的变量视为潜在的混杂因子。
目前,DoWhy 支持如下形式的因果假设:
图 (Graph):提供 gml 或 dot 形式的因果图,具体可以是文件或字符串格式命名变量集合 (Named variable sets):直接提供变量的类型,包括混杂因子 (common causes / cofounders)、工具变量 (instrumental variables)、结果修改变量 (effect modifiers)、前门变量 (front-door variables)等
识别
基于构建的因果图,DoWhy 会基于所有可能的方式来识别因果效应。具体来说,会使用基于图的准则与 do-积分 来找出可以识别因果效应的表达式,支持的识别准则有:
后门准则 (Back-door criterion)前门准则 (Front-door criterion)工具变量 (Instrumental Variables)中介-直接或间接结果识别 (Mediation-Direct and indirect effect identification)
估计
DoWhy 支持一系列基于上述识别准则的估计方法,此外还提供了非参数置信空间与排列测试来检验得到的估计的统计显著性。具体支持的估计方法列表如下:
基于估计干预分配的方法
基于倾向的分层(Propensity-based Stratification)
倾向得分匹配(Propensity Score Matching)
逆向倾向加权(Inverse Propensity Weighting)
基于估计结果模型的方法
线性回归(Linear Regression)
广义线性模型(Generalized Linear Models)
基于工具变量等式的方法
二元工具/Wald 估计器(Binary Instrument/Wald Estimator)
两阶段最小二乘法(Two-stage least squares)
非连续回归(Regression discontinuity)
基于前门准则和一般中介的方法
两层线性回归(Two-stage linear regression)
此外,DoWhy 还支持调用外部的估计方法,例如 EconML 与 CausalML。
反驳
DoWhy 支持多种反驳方法来验证估计的正确性,具体列表如下:
添加随机混杂因子 :添加一个随机变量作为混杂因子后估计因果效应是否会改变(期望结果:不会)安慰剂干预 :将真实干预变量替换为独立随机变量后因果效应是否会改变(期望结果:因果效应归零)虚拟结果 :将真实结果变量替换为独立随机变量后因果效应是否会改变(期望结果:因果效应归零)模拟结果 :将数据集替换为基于接近给定数据集数据生成过程的方式模拟生成的数据集后因果效应是否会改变(期望结果:与数据生成过程的效应参数相匹配)添加未观测混杂因子 :添加一个额外的与干预和结果相关的混杂因子后因果效应的敏感性(期望结果:不过度敏感)数据子集验证 :将给定数据集替换为一个随机子集后因果效应是否会改变(期望结果:不会)自助验证 :将给定数据集替换为同一数据集的自助样本后因果效应是否会改变(期望结果:不会)
入门案例
下面将通过一个简单的例子说明 DoWhy 的工作流程。我们将读取一个样本数据集并估计一个干预变量对一个结果变量的因果效应。
安装
DoWhy 的安装很简单,直接基于 pip 安装发行版即可:
其他安装选项与注意事项请自行查阅官方说明。为了更好地展示图,推荐安装 pygraphviz,Mac OS 下安装方法如下:
brew install graphviz pip install pygraphviz
包导入与数据载入
安装完成后,导入相关的包并配置路径:
import os, syssys.path.append(os.path.abspath("../../../" )) import numpy as npimport pandas as pdimport dowhyfrom dowhy import CausalModelimport dowhy.datasets
然后导入数据集。本例中为了简单我们模拟了不同变量之间的线性 关系。具体代码如下:
data = dowhy.datasets.linear_dataset(beta=10 , num_common_causes=5 , num_instruments=2 , num_effect_modifiers=1 , num_samples=10000 , treatment_is_binary=True , num_discrete_common_causes=1 ) df = data["df" ] print (df.head())print (data["dot_graph" ])
代码的输出如下:
X0 Z0 Z1 W0 W1 W2 W3 W4 v0 \ 0 1.418641 0.0 0.251127 0.237823 1.294957 -2.197657 0.671354 1 True 1 0.050088 0.0 0.041706 -1.199278 3.143332 -1.738985 -2.766051 1 False 2 -0.480051 0.0 0.974275 -1.957273 -0.065116 0.175567 -1.829176 1 True 3 0.338169 1.0 0.727792 -0.245409 0.099252 0.998839 -0.870295 0 True 4 -1.026205 0.0 0.983040 -0.147827 1.538178 0.441017 0.343857 2 True y 0 19.477585 1 -5.857091 2 2.179680 3 7.307447 4 15.688496 digraph { U[label="Unobserved Confounders" ]; U->y;v0->y; U->v0;W0-> v0; W1-> v0; W2-> v0; W3-> v0; W4-> v0;Z0-> v0; Z1-> v0;W0-> y; W1-> y; W2-> y; W3-> y; W4-> y;X0-> y;}
执行因果推断
建模
现在我们以 GML 图的形式构建因果图(建模阶段 ),代码如下:
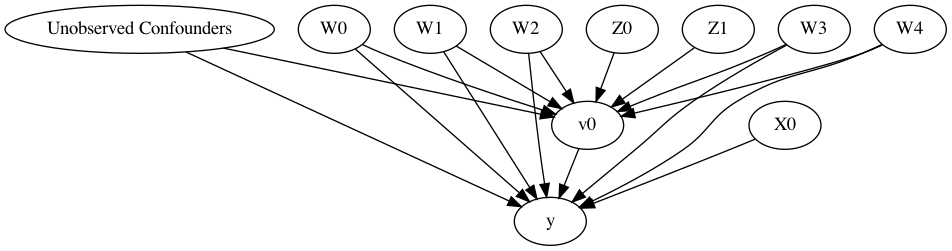
model=CausalModel( data = df, treatment=data["treatment_name" ], outcome=data["outcome_name" ], graph=data["gml_graph" ] ) model.view_model() from IPython.display import Image, displaydisplay(Image(filename="causal_model.png" ))
执行代码可以得到如下的因果图:
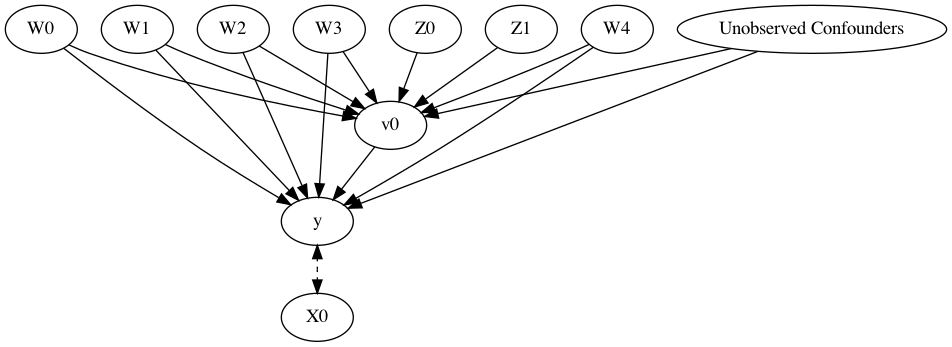
我们也可以通过指定具体变量的方式来生成图(本例中由于数据是模拟的,所以各种方式均可以生成),代码如下:
model= CausalModel( data=df, treatment=data["treatment_name" ], outcome=data["outcome_name" ], instruments=data["instrument_names" ], common_causes=data["common_causes_names" ], effect_modifiers=data["effect_modifier_names" ])
得到的图与上一张实际上是等价的:
上图包含了数据中给定的先验知识(变量分类),我们可以利用这张图来识别因果效应(从因果估计量到概率表达式)并进行估计。
识别
识别阶段 可以脱离于数据,仅根据图进行识别,其给出的结果是一个用于计算的表达式 。具体的代码如下:
identified_estimand = model.identify_effect() print (identified_estimand)
输出结果为:
Estimand type : nonparametric-ate Estimand name: backdoor1 Estimand expression: d ─────(Expectation(y|W1,W2,W3,W0,W4)) d[v₀] Estimand assumption 1 , Unconfoundedness: If U→{v0} and U→y then P(y|v0,W1,W2,W3,W0,W4,U) = P(y|v0,W1,W2,W3,W0,W4) Estimand name: backdoor2 (Default) Estimand expression: d ─────(Expectation(y|W1,W2,W3,W0,W4,X0)) d[v₀] Estimand assumption 1 , Unconfoundedness: If U→{v0} and U→y then P(y|v0,W1,W2,W3,W0,W4,X0,U) = P(y|v0,W1,W2,W3,W0,W4,X0) Estimand name: iv Estimand expression: Expectation(Derivative(y, [Z0, Z1])*Derivative([v0], [Z0, Z1])**(-1 )) Estimand assumption 1 , As-if -random: If U→→y then ¬(U →→{Z0,Z1}) Estimand assumption 2 , Exclusion: If we remove {Z0,Z1}→{v0}, then ¬({Z0,Z1}→y)
可以通过 proceed_when_unidentifiable=True 参数来忽略观察性数据中未观测混杂因子的 warning。
估计
识别阶段得到的表达式将在估计阶段 基于实际数据进行计算,注意这两个阶段是独立开来的。估计的代码如下:
causal_estimate = model.estimate_effect(identified_estimand, method_name="backdoor.propensity_score_stratification" ) print (causal_estimate)print ("Causal Estimate is " + str (causal_estimate.value))
输出的结果为:
*** Causal Estimate *** Estimand type : nonparametric-ate b: y~v0+W1+W2+W3+W0+W4+X0 Target units: ate Mean value: 8.937706276657458 Causal Estimate is 8.937706276657458
我们可以通过 target_units 参数来选择因果效应分析的群体,如 ate(群体层面)、att(干预组)、ate(对照组)。也可以指定结果修改变量来分析不同变量对结果的影响。
反驳
下面给出一些对得到的估计进行反驳的方式:
添加一个随机的混杂因子变量
res_random=model.refute_estimate(identified_estimand, causal_estimate, method_name="random_common_cause" ) print (res_random)
Refute: Add a Random Common Cause Estimated effect:9.124260741049653 New effect:9.13487620983324
添加一个未观测的混杂因子变量
res_unobserved=model.refute_estimate(identified_estimand, causal_estimate, method_name="add_unobserved_common_cause" , confounders_effect_on_treatment="binary_flip" , confounders_effect_on_outcome="linear" , effect_strength_on_treatment=0.01 , effect_strength_on_outcome=0.02 ) print (res_unobserved)
Refute: Add an Unobserved Common Cause Estimated effect:9.124260741049653 New effect:8.129085846396725
用随机变量代替干预
res_placebo=model.refute_estimate(identified_estimand, causal_estimate, method_name="placebo_treatment_refuter" , placebo_type="permute" ) print (res_placebo)
Refute: Use a Placebo Treatment Estimated effect:9.124260741049653 New effect:-0.010832019791737903 p value:0.48
移除数据的一个随机子集
res_subset=model.refute_estimate(identified_estimand, estimate, method_name="data_subset_refuter" , subset_fraction=0.9 ) print (res_subset)
Refute: Use a subset of data Estimated effect:9.124260741049653 New effect:9.090515505813006 p value:0.37
我们可以通过 random_seed 参数来保证结果的可重现性。
进阶案例
问题描述
下面将通过一个基于真实世界数据的案例对 DoWhy 的工作流程进行进一步说明。在本例中,我们的研究问题是估计当消费者在预定酒店时,为其分配一间与之前预定过的房间不同的房间对消费者取消当前预定的影响。分析此类问题的金标准是随机对照试验 (Randomized Controlled Trials),即每位消费者被随机分配到两类干预中的一类:为其分配与之前预定过的房间相同或不同的房间。
然而,实际上对于酒店来说其不可能进行这样的试验,只能使用历史数据(观察性数据)来进行评估。我们首先导入相关包与数据集:
import dowhyimport pandas as pdimport numpy as npimport matplotlib.pyplot as pltimport logginglogging.getLogger("dowhy" ).setLevel(logging.INFO) dataset = pd.read_csv('https://raw.githubusercontent.com/Sid-darthvader/DoWhy-The-Causal-Story-Behind-Hotel-Booking-Cancellations/master/hotel_bookings.csv' ) dataset.columns
该数据集包含如下参数:
Index(['hotel' , 'is_canceled' , 'lead_time' , 'arrival_date_year' , 'arrival_date_month' , 'arrival_date_week_number' , 'arrival_date_day_of_month' , 'stays_in_weekend_nights' , 'stays_in_week_nights' , 'adults' , 'children' , 'babies' , 'meal' , 'country' , 'market_segment' , 'distribution_channel' , 'is_repeated_guest' , 'previous_cancellations' , 'previous_bookings_not_canceled' , 'reserved_room_type' , 'assigned_room_type' , 'booking_changes' , 'deposit_type' , 'agent' , 'company' , 'days_in_waiting_list' , 'customer_type' , 'adr' , 'required_car_parking_spaces' , 'total_of_special_requests' , 'reservation_status' , 'reservation_status_date' ], dtype='object' )
关于数据的详细描述可以参考此链接 。
数据预处理
下面我们将创建一些有用的特征,来减少原始数据的维度。具体来说,我们将创建如下三个特征:
Total Stay = stays_in_weekend_nights + stays_in_week_nightsGuests = adults + children + babiesDifferent_room_assigned = 1 if reserved_room_type & assigned_room_type are different, 0 otherwise
具体创建过程如下(很基础的 pandas 操作,不过多赘述):
dataset['total_stay' ] = dataset['stays_in_week_nights' ]+dataset['stays_in_weekend_nights' ] dataset['guests' ] = dataset['adults' ]+dataset['children' ] +dataset['babies' ] dataset['different_room_assigned' ]=0 slice_indices =dataset['reserved_room_type' ]!=dataset['assigned_room_type' ] dataset.loc[slice_indices,'different_room_assigned' ]=1 dataset = dataset.drop(['stays_in_week_nights' ,'stays_in_weekend_nights' ,'adults' ,'children' ,'babies' ,'reserved_room_type' ,'assigned_room_type' ],axis=1 )
之后再对缺失值与布尔值进行预处理,并去除部分特征:
dataset.isnull().sum () dataset = dataset.drop(['agent' ,'company' ],axis=1 ) dataset['country' ]= dataset['country' ].fillna(dataset['country' ].mode()[0 ]) dataset = dataset.drop(['reservation_status' ,'reservation_status_date' ,'arrival_date_day_of_month' ],axis=1 ) dataset = dataset.drop(['arrival_date_year' ],axis=1 ) dataset['different_room_assigned' ]= dataset['different_room_assigned' ].replace(1 ,True ) dataset['different_room_assigned' ]= dataset['different_room_assigned' ].replace(0 ,False ) dataset['is_canceled' ]= dataset['is_canceled' ].replace(1 ,True ) dataset['is_canceled' ]= dataset['is_canceled' ].replace(0 ,False ) dataset.dropna(inplace=True ) dataset.columns
处理完成后的参数有:
Index(['hotel' , 'is_canceled' , 'lead_time' , 'arrival_date_month' , 'arrival_date_week_number' , 'meal' , 'country' , 'market_segment' , 'distribution_channel' , 'is_repeated_guest' , 'previous_cancellations' , 'previous_bookings_not_canceled' , 'booking_changes' , 'deposit_type' , 'days_in_waiting_list' , 'customer_type' , 'adr' , 'required_car_parking_spaces' , 'total_of_special_requests' , 'total_stay' , 'guests' , 'different_room_assigned' ], dtype='object' )
提取假设
数据预处理完成后,我们首先针对数据进行一定的分析,考察变量之间的关系。针对目标变量 is_cancelled 与 different_room_assigned ,我们随机选取 1000 次观测查看有多少次上述两个变量的值相同(即可能存在因果关系),重复上述过程 10000 次取平均,代码如下:
counts_sum=0 for i in range (1 ,10000 ): counts_i = 0 rdf = dataset.sample(1000 ) counts_i = rdf[rdf["is_canceled" ]== rdf["different_room_assigned" ]].shape[0 ] counts_sum+= counts_i counts_sum/10000
最终得出的期望频数是 518 ,即两个变量有约 50% 的时间是不同的,我们还无法判断其中的因果关系。下面我们进一步分析预约过程中没有发生调整时(即变量 booking_changes 为 0) 两个变量相等的期望频数:
counts_sum=0 for i in range (1 ,10000 ): counts_i = 0 rdf = dataset[dataset["booking_changes" ]==0 ].sample(1000 ) counts_i = rdf[rdf["is_canceled" ]== rdf["different_room_assigned" ]].shape[0 ] counts_sum+= counts_i counts_sum/10000
得出的结果为 492 。随后我们再分析预约过程中发生调整时的期望频数:
counts_sum=0 for i in range (1 ,10000 ): counts_i = 0 rdf = dataset[dataset["booking_changes" ]>0 ].sample(1000 ) counts_i = rdf[rdf["is_canceled" ]== rdf["different_room_assigned" ]].shape[0 ] counts_sum+= counts_i counts_sum/10000
结果变成了 663 ,与之前产生了明显的差异。我们可以不严谨地认为预约调整这一变量是一个混杂因子 。类似地,我们对其他变量进行分析,并作出一些假设,作为因果推断的先验知识。DoWhy 并不需要完整的先验知识,未指明的变量将作为潜在的混杂因子进行推断。在本例中,我们将给出如下的假设:
market_segment 参数有两种取值:TA 指旅行者,TO 指旅游公司,该参数会影响 lead_time(即预约和到达之间的时间间隔)country 参数会决定一个人是否会提早预订(即影响 lead_time )以及其喜爱的食物(即影响 meal )lead_time 会影响预订的等待时间( days_in_waiting_list )预订的等待时间 days_in_waiting_list、总停留时间 total_stay 以及客人数量 guests 会影响预订是否被取消
之前预订的取消情况 previous_bookings_not_canceled 会影响该顾客是否为 is_repeated_guest;这两个变量也会影响预订是否被取消
booking_changes 会影响顾客是否被分配到不同的房间,也会影响预订取消情况除了 booking_changes 这一混杂因子外,一定还存在着其他混杂因子,同时影响干预和结果
因果推断
创建因果图
基于上述假设,我们通过 gml 形式来描述上述因果图:
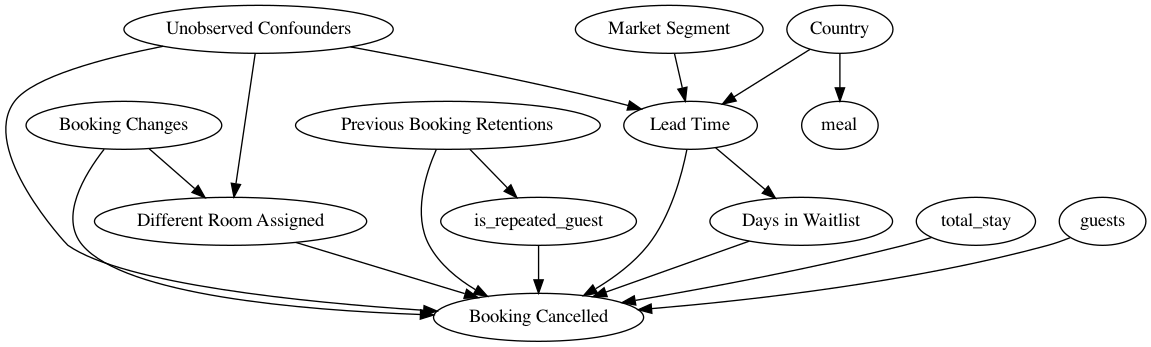
import pygraphvizcausal_graph = """digraph { different_room_assigned[label="Different Room Assigned"]; is_canceled[label="Booking Cancelled"]; booking_changes[label="Booking Changes"]; previous_bookings_not_canceled[label="Previous Booking Retentions"]; days_in_waiting_list[label="Days in Waitlist"]; lead_time[label="Lead Time"]; market_segment[label="Market Segment"]; country[label="Country"]; U[label="Unobserved Confounders"]; is_repeated_guest; total_stay; guests; meal; market_segment -> lead_time; lead_time->is_canceled; country -> lead_time; different_room_assigned -> is_canceled; U -> different_room_assigned; U -> lead_time; U -> is_canceled; country->meal; lead_time -> days_in_waiting_list; days_in_waiting_list ->is_canceled; previous_bookings_not_canceled -> is_canceled; previous_bookings_not_canceled -> is_repeated_guest; is_repeated_guest -> is_canceled; total_stay -> is_canceled; guests -> is_canceled; booking_changes -> different_room_assigned; booking_changes -> is_canceled; }"""
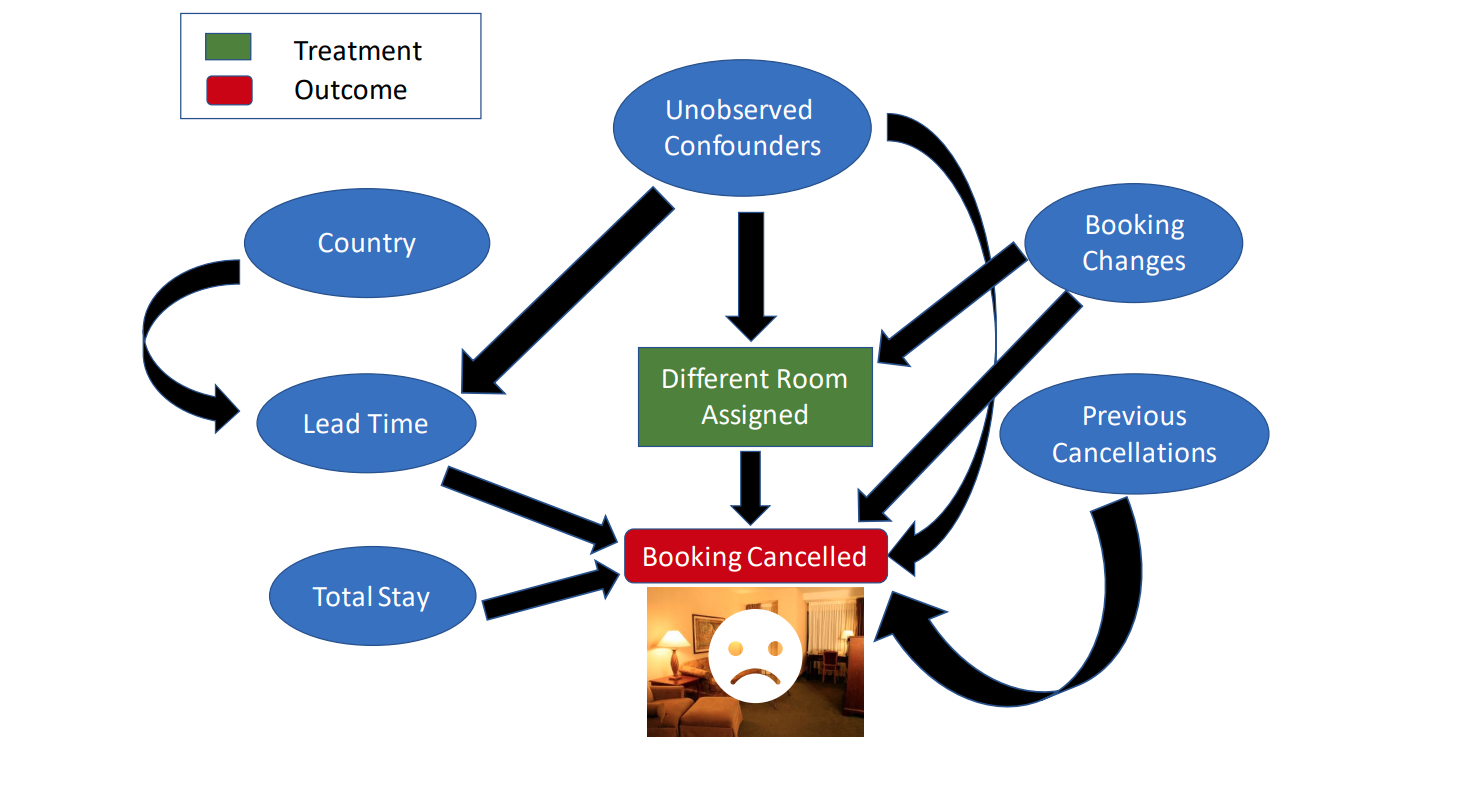
基于上述图,可以构建出如下的因果模型:
model= dowhy.CausalModel( data = dataset, graph=causal_graph.replace("\n" , " " ), treatment='different_room_assigned' , outcome='is_canceled' ) model.view_model() from IPython.display import Image, displaydisplay(Image(filename="causal_model.png" ))
识别因果效应
我们称干预 (Treatment)导致了结果 (Outcome)当且仅当在其他所有状况不变的情况下,干预的改变引起了结果的改变。因果效应即干预发生一个单位的改变时,结果变化的程度。下面我们将使用因果图的属性来识别因果效应的估计量。
identified_estimand = model.identify_effect() print (identified_estimand)
注意,在最新版本的 dowhy 中,修改了识别阶段后门变量的筛选准则,从原来的选择最小集改为了选择所有合法的变量,因此最终会返回 258 个估计量(此处参见 issue-198 )。如下所示为返回的估计量示例:
Estimand type : nonparametric-ate Estimand name: backdoor1 Estimand expression: d ──────────────────────────(Expectation(is_canceled|lead_time,booking_changes)) d[different_room_assigned] Estimand assumption 1 , Unconfoundedness: If U→{different_room_assigned} and U→is_canceled then P(is_canceled|different_room_assigned,lead_time,booking_changes,U) = P(is_canceled|different_room_assigned,lead_time,booking_changes)
估计因果效应
基于估计量,下面我们就可以根据实际数据进行因果效应的估计了。如之前所述,因果效应即干预进行单位改变时结果的变化程度。DoWhy 支持采用各种各样的方法计算因果效应估计量,并最终返回单个平均值。代码如下所示:
estimate = model.estimate_effect(identified_estimand, method_name="backdoor.propensity_score_stratification" ,target_units="ate" ) print (estimate)
这里我们选择估计平均干预效应(ATE),也可以选择估计干预组(ATT)或对照组(ATC)的因果效应。估计方法选择的是倾向得分匹配 ,具体的原理这里不做介绍。最终得到的结果如下:
*** Causal Estimate *** Estimand type : nonparametric-ate b: is_canceled~different_room_assigned+country+total_stay+meal+lead_time+guests+days_in_waiting_list+booking_changes+market_segment+is_repeated_guest+previous_bookings_not_canceled Target units: ate Mean value: -0.3359905635051836
反驳结果
实际上,上述因果并不是基于数据,而是基于我们所做的假设(即提供的因果图),数据只是用于进行统计学的估计。因此,我们需要验证假设的正确性。DoWhy 支持通过各种各样的鲁棒性检查方法来测试假设的正确性。下面进行其中几项测试:
添加随机混杂因子 。如果假设正确,则添加随机的混杂因子后,因果效应不会变化太多。
refute1_results=model.refute_estimate(identified_estimand, estimate, method_name="random_common_cause" ) print (refute1_results)
Refute: Add a Random Common Cause Estimated effect:-0.3359905635051836 New effect:-0.3365742386420179
安慰剂干预 。将干预替换为随机变量,如果假设正确,因果效应应该接近 0。
refute2_results=model.refute_estimate(identified_estimand, estimate, method_name="placebo_treatment_refuter" ) print (refute2_results)
Refute: Use a Placebo Treatment Estimated effect:-0.3359905635051836 New effect:-0.00028277666065981027 p value:0.43999999999999995
注意:这里的 p value 对比的是新的估计量与 0 之间的显著性差异(如果假设正确,则预期为无差异),源代码如下:
dummy_estimator = CausalEstimate( estimate = 0 , target_estimand =self._estimate.target_estimand, realized_estimand_expr=self._estimate.realized_estimand_expr) refute.add_significance_test_results( self.test_significance(dummy_estimator, sample_estimates) )
数据子集验证 。在数据子集上估计因果效应,如果假设正确,因果效应应该变化不大。
refute3_results=model.refute_estimate(identified_estimand, estimate, method_name="data_subset_refuter" ) print (refute3_results)
Refute: Use a subset of data Estimated effect:-0.3359905635051836 New effect:-0.33647521997465524 p value:0.35
可以看到,我们的因果模型基本可以通过上述几个测试(即取得预期的结果)。因此,根据估计阶段的结果,我们得出结论:当消费者在预定房间时,为其分配之前预定过的房间( different_room_assigned = 0 )所导致的平均预定取消概率( is_canceled )要比为其分配不同的房间( different_room_assigned = 1 )低 33% (感觉应该是正值?好像是有问题,已提 issue )。
在实际的操作中,我们可以基于不同的假设(即不同的因果图)应用多种估计方法,以找出接近真实的因果关系。
结果比较
综上所述,我们已经知道了分配不同的房间的因果效应约为 33%,下面我们将使用一个预测模型对数据进行训练,并分析不同特征的特征重要性。这里选择 XGBoost 作为预测模型,其训练过程及结果如下:
from xgboost import XGBClassifierfrom xgboost import plot_importancefrom sklearn.model_selection import train_test_splitfrom sklearn.metrics import accuracy_score, classification_reportfrom matplotlib import pyplotX = dataset_copy y = dataset_copy['is_canceled' ] X = X.drop(['is_canceled' ],axis=1 ) X = pd.get_dummies(X) X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2 , random_state=26 ) model = XGBClassifier() model.fit(X_train, y_train) y_pred = model.predict(X_test) predictions = [int (value) for value in y_pred] accuracy = accuracy_score(y_test, predictions) print ("Accuracy: %.2f%%" % (accuracy * 100.0 ))print (classification_report(y_test, predictions))
Accuracy: 86.40% precision recall f1-score support False 0.88 0.92 0.90 15001 True 0.85 0.79 0.82 8877 accuracy 0.87 23878 macro avg 0.86 0.85 0.86 23878 weighted avg 0.867 0.87 0.87 23878
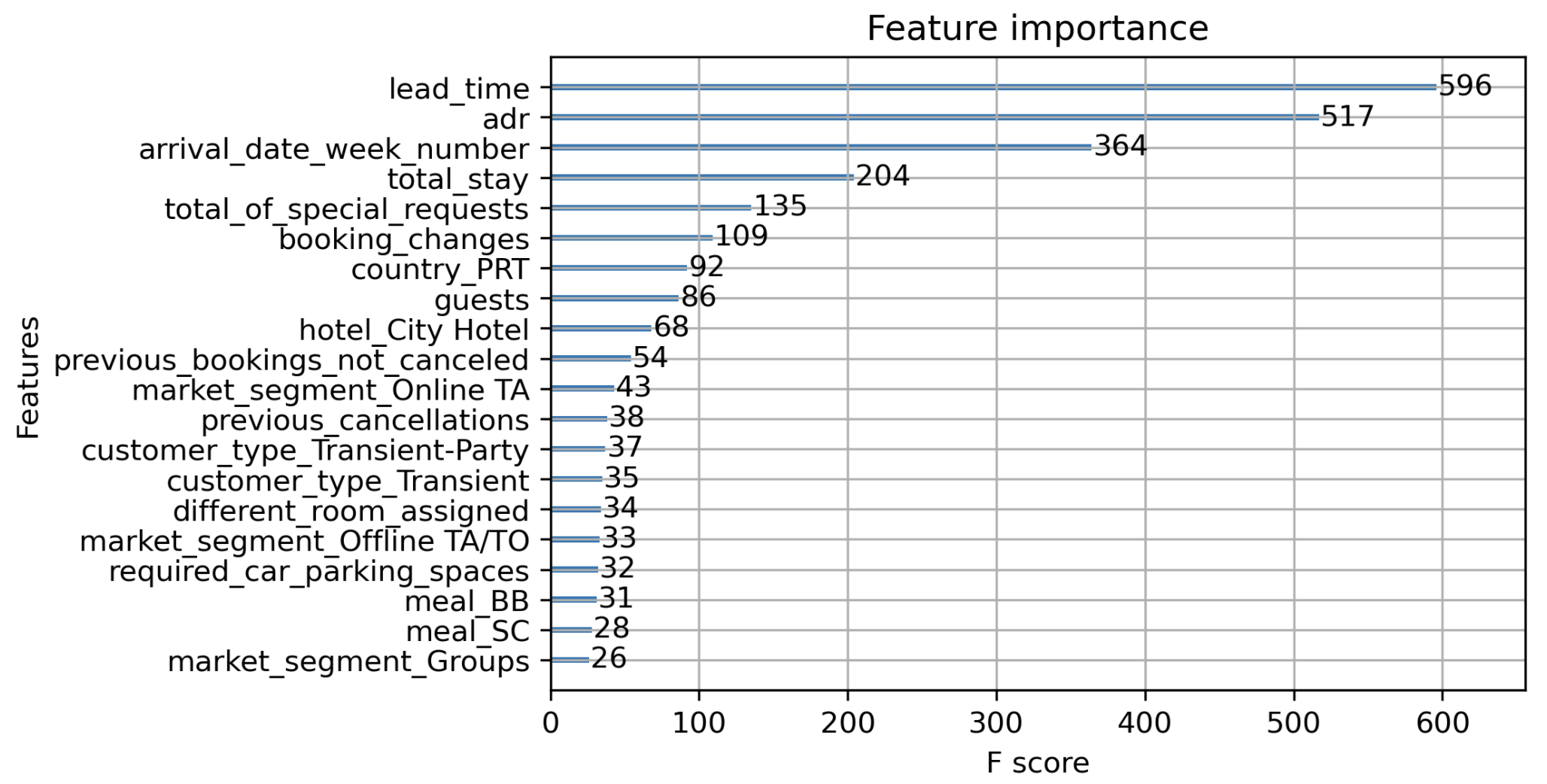
利用 plot_importance 函数,可以得出如下的特征重要性排行(这里权重值为特征在树中出现的次数):
plot_importance(model,max_num_features=20 ) pyplot.show()
可以看出,different_room_assigned 变量的特征权重并不是非常高,这与我们的因果推断结果有一定的差异性,这也体现了因果推断模型和传统机器学习模型在原理上的差异性,我们需要根据实际的需要来选择最合适的方法。
以上就是 DoWhy 入门的全部内容,总的来看, DoWhy 为因果推断研究提供了一个非常方便的工具,研究人员需要做的就是先对数据进行分析并给出适当的假设(可以是多个),然后将数据输入到 DoWhy 提供的框架中进行自动化估计(需要指定估计方法与估计目标),最后对估计的结果进行鲁棒性测试以验证假设的正确性,即可得出较为合理的因果关系推论。
注:本文参考自 DoWhy 的官方文档 。