监督学习简明指南

本篇博客为基于 CS229 对监督学习的总结。

监督学习简介

给定一组数据点 \(\{x^{(1)},...,x^{(m)}\}\) 和与其对应的输出 \(\{y^{(1)},...,y^{(m)}\}\)， 监督学习的目的是建立一个模型来学习如何从 \(x\) 预测 \(y\)

预测的类型

根据预测的输出是否连续，可以将监督学习分为回归问题和分类问题：

模型的类型

根据模型本身的特点，可以分为判别模型和生成模型，具体区别如下表所示：

符号和一般概念

假设函数

假设函数即我们所选择的模型，符号表示为 \(h_\theta\)，给定输入数据 \(x^{(i)}\)，模型的预测输出是 \(h_\theta\left(x^{(i)}\right)\)

损失函数

损失函数（Loss Function）是一个 \((z,y) \in \mathbb{R} \times Y \longmapsto L(z,y) \in \mathbb{R}\) 的函数，其将真实数据值 \(y\) 和其预测值 \(z\) 作为输入，输出它们的不同程度。

常见的损失函数如下表所示：

表中的例子并不一定绝对（逻辑回归一般使用交叉熵作为代价函数）。

代价函数

代价函数（Cost Function）通常用于估计模型的性能，其可以看做是损失函数在所有样本上的总和： \[ J(\theta) = \sum_{i=1}^m L(h_{\theta}(x^{(i)}),y^{(i)}) \]

根据实际情况，可能需要取平均（加上 \(\frac 1 m\)）。

似然函数

一个模型的似然函数 \(L(\theta)\) 用于通过最大似然估计来找到最优参数 \(\theta\)： \[ \theta^{\,\text{opt}} = \arg \max_\theta L(\theta) \]

很多模型的代价函数就是通过最大似然法（最大化似然函数等价于最小化代价函数）得出的。在实践中，我们通常使用更加容易优化的对数似然函数来执行优化： \[ \ell(\theta) = \log(L(\theta)) \]

梯度下降

梯度下降是一种迭代方法，用来求解使得代价函数最小化（或似然函数最大化）的参数近似值。

记学习率为 \(\alpha \in \mathbb{R}\)，梯度下降的更新规则如下： \[ \theta \leftarrow \theta - \alpha \nabla J(\theta) \]

根据每次更新的样本个数，梯度下降可以分为两类：

• 随机梯度下降（SGD）：指每次使用一个训练样本进行参数更新
• 批量梯度下降：指每次在一批训练样本上进行更新

牛顿算法

牛顿算法也是一种迭代方法，目的是找到使得 \(\ell'(\theta)=0\) 的 \(\theta\)，其更新规则如下： \[ \theta \leftarrow \theta - \frac {\ell'(\theta)} {\ell''(\theta)} \] 其多维形式，也称为 Newton-Raphson 方法，具有如下的更新规则： \[ \theta \leftarrow \theta - H^{-1}\nabla_\theta\ell(\theta) \]

其中 \(H\) 是一个 \((n+1)\times(n+1)\) 的矩阵，其中的每一项定义为： \[ H_{ij}=\frac {\partial^2 \ell(\theta)} {\partial \theta_i \partial \theta_j} \]

线性回归

算法简介

线性回归是一种监督学习算法，输出变量连续，其假设函数与代价函数如下：

假设函数为： \[ h_\theta(x) = \sum_{i=0}^n\theta_ix_i = \theta^Tx \] 代价函数为： \[ J(\theta) = \frac 1 2 \sum_{i=1}^m \left(h_\theta(x^{(i)})-y^{(i)}\right)^2 \] 线性回归的学习目标是通过训练集找出使代价函数最小的一组参数 \(\theta\)（又称最小二乘法）。

求解方法

代价函数求解的方法有两种：梯度下降 & 正规方程。

梯度下降

梯度下降基于 \(\alpha\) 学习率，不断更新参数逼近最优解： \[ \theta_j := \theta_j+\alpha\left(y^{(i)}-h_\theta(x^{(i)})\right)x^{(i)}_j \]

正规方程

通过设计 \(X\) 矩阵，直接求出 \(\theta\) 的解析解： \[ \theta=(X^TX)^{-1}X^T\vec y \]

概率解释

对于线性回归，真实值可以看做以预测值为中心的正态分布： \[ y^{(i)} \,\rvert \,x^{(i)};\theta\sim {\cal N }(\theta^Tx^{(i)},\sigma^2) \] 基于该概率解释，通过最大似然法，我们可以推导出之前定义的最小二乘代价函数。

局部加权线性回归

LWR 是线性回归的变式，通过非负权重 \(\omega^{(i)}\) 对代价函数中的每个训练样本进行加权，一般取值如下： \[ \omega^{(i)}=exp\left(-\frac{(x^{(i)}-x)^2}{2\tau^2}\right) \] 其本质上是一种非参数学习算法（参数不固定，需要保存完整的训练集来进行预测，而非仅仅保存参数）。

逻辑回归

算法简介

将线性回归模型直接应用于分类问题，会产生取值不在 0 和 1 之间的问题，所以我们引入逻辑回归模型： \[ h_{\theta}(x) = g(\theta^Tx) = \frac 1 {1+e^{-\theta^Tx}} \]

其中 \[ g(z) = \frac 1 {1+e^{-z}} \] \(g(z)\) 被称为逻辑函数或 S 型函数，其图像如下：

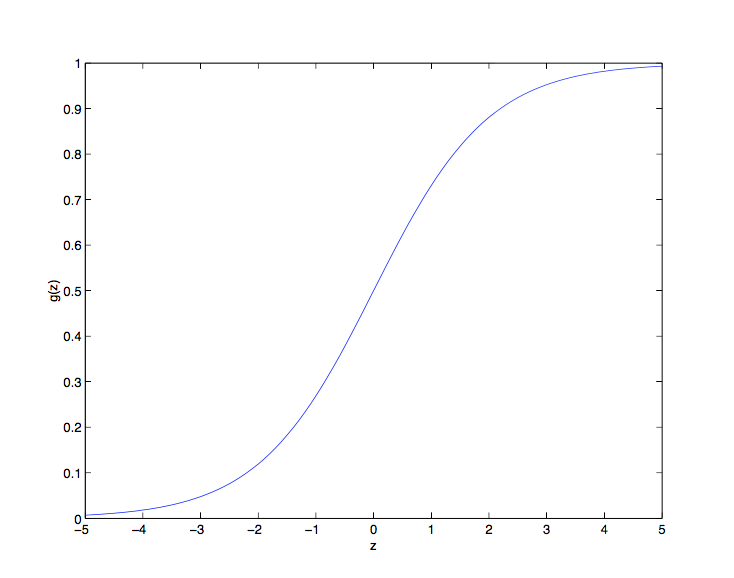
确定了模型之后，我们需要找到合适的 \(\theta\) 的值。二元分类符合伯努利分布： \[ \begin{align*} P(y=1 \mid x ;\theta) &= h_{\theta}(x)\\ P(y=0 \mid x ;\theta) &= 1-h_{\theta}(x) \end{align*} \] 将上面的公式合二为一，得到： \[ P(y \mid x ; \theta) = (h_{\theta}(x))^y(1-h_{\theta}(x))^{1-y} \] 通过对数似然函数进行最大化分析，最终可以基于梯度上升求得如下更新规则： \[ \theta_j := \theta_j +\alpha\left(y^{(i)}-h_\theta(x^{(i)})\right)x^{(i)}_j \]

Softmax 回归

当存在超过 2 个结果类时，使用 softmax 回归（也称为多类逻辑回归）来推广逻辑回归，其符合多项分布，对应的概率公式为（为了方便，我们定义\(\theta_k = 0\)，实际上第 \(k\) 个输出的概率可以用其他 \(k-1\) 个输出的概率来表示）： \[ \begin{align*} p(y=i \mid x;\theta) &= \phi_i \\ &= \frac{e^{\eta_i}}{\sum_{j=1}^k e^{\eta_j} } \\ &= \frac{e^{\theta_i^T x}}{\sum_{j=1}^k e^{\theta_j^T x} } \end{align*} \]

广义线性模型

上述模型都是一个更为广泛的模型族的特例，这个模型族被称为广义线性模型（Generalized Linear Models）。为了引出广义线性模型，我们首先需要介绍指数族分布：

如果一个分布可以被表示成如下形式，我们就称其属于指数分布族： \[ p(y;\eta) =b(y) \exp \left( \eta ^{T}T(y)-a(\eta)\right) \qquad(1) \]

• \(\eta\) 被称为分布的自然参数（或者称为典范参数）
• \(T(y)\) 被称为充分统计量，通常 \(T(y)=y\)
• \(a(\eta)\) 被称为对数分割函数
• \(e^{-a(\eta)}\) 本质上是一个归一化常数，确保概率 \(p(y;\eta)\) 和为 1

当选定 \(T,a,b\) 时，我们就得到了一种以 \(\eta\) 为参数的分布。下表总结了最常见的指数族分布：

| 分布

\(\eta\)	\(T(y)\)	\(a(\eta)\)	\(b(y)\)
伯努利	\(\log\left(\frac \phi {1-\phi}\right)\)	\(y\)	\(\log(1+e^{\eta})\)	1
多项	\(\left[\begin{array}{c}\log \left(\phi_1 / \phi_k\right) \\ \log \left(\phi_1 / \phi_k\right) \\ \vdots \\ \log \left(\phi_{k-1} / \phi_k\right)\end{array}\right]\)	\(1\{y=i\}\)	\(-\log(\phi_k)\)	1
高斯	\(\mu\)	\(y\)	\(\eta^2\)	\(\frac{1}{\sqrt{2 \pi}} \exp \left(-\frac{y^2}{2}\right)\)
泊松	\(\log(\lambda)\)	\(y\)	\(e^{\eta}\)	\(\frac {1} {y!}\)
几何	\(\log(1-\phi)\)	y	\(\log\left(\frac {e^{\eta}} {1-e^{\eta}}\right)\)	1

基于指数族分布，可以构建广义线性模型，其旨在将随机变量 \(y\) 预测为 \(x \in \mathbb{R}^{n+1}\) 的函数，需要依赖以下三个假设：

1. \(y\mid x;\theta\) 符合以 \(\eta\) 为参数的指数族分布
2. \(h_\theta(x)=E[y \mid x ; \theta]\)（假设函数的预测目标是 \(T(y)\) 的理想值）
3. 自然参数 \(\eta\) 和 输入 \(x\) 满足线性关系 \(\eta=\theta^T x\)

基于上述三条假设，我们可以推导出之前介绍模型的假设函数（此处省略）。

支持向量机

待完成

生成学习

待完成

基于树的方法和集成方法

待完成

其他非参数方法

待完成

学习理论

待完成

本文部分素材来源于 Afshine 和 Shervine 分享的 Cheatsheet